студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy

8.5 ] Дифракция Фраунгофера 581

Интерес, как правило, представляет область значений в плоскости наблюдения , размер которой мал в сравнении

с , поэтому и

#

40

Используя найденные значения 40 и 40 , получаем следующее приближение: 4 2 4 40 2. Теперь решение дифракционной задачи выражается формулой:

1 6 40 4 40 3 вносит пренебрежимо малую поправку. После замены переменных 4 40 получаем

(стационарной точке соответствует значение 0). Напомним,

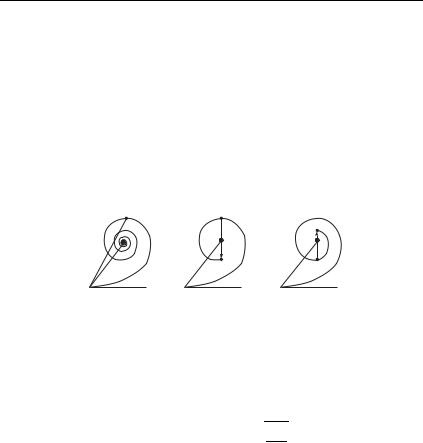
В нашем случае # 2 , причем основной вклад в интеграл определяется длиной одного полувитка спирали: вектор, проведенный из начала спирали (точка O) в конец первого полувитка (точка 1), мало отличается по длине и направлению от вектора, проведенного в фокус спирали (рис. 8.11). Точке 1 соответствует область интегрирования, определяемая условием

Фокусам спирали соответствуют бесконечные пределы интегрирования, откуда следует оценка

Потребуем теперь, чтобы в области интегрирования (окрестности стационарной точки) ' 1 функция %0 40

8.6 ] Принцип Гюйгенса–Френеля 583

Последний интеграл представляет собой сумму антиколлинеар-

ных векторов 1 и , пренебрежимо малую в сравнении

2 2 3

с вектором, проведенным из начала в фокус спирали. Понятно, что если спектр %0 4 описывается достаточно плавно меняющейся функцией, то вкладом области интегрирования & 1 можно пренебречь и окончательно, с учетом (8.39), (8.40) и имея ввиду (8.35), получаем

Напомним, что область применимости граничных условий Кирхгофа: и, так как ' , то ясно, что полученное нами приближение справедливо.

Итак, мы получили чрезвычайно простой способ определения дифракционной картины Фраунгофера. Поле в точке наблюдения

2

, , удаленной в область ) , определяется значением спек-

тра %0 4 граничного поля в стационарной точке 40 . Более детально дифракция Фраунгофера будет исследована в § 8.9.

8.6. Принцип Гюйгенса–Френеля

Принцип Гюйгенса–Френеля является рецептом для решения дифракционных задач, отличным от изложенного выше спектрального подхода.

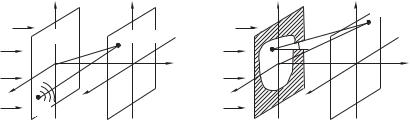
Пусть волна света, созданная источниками, расположенными в области ' 0, достигла плоскости 0 (каких-либо препятствий на пути света пока еще нет; рис. 8.12 а). Световое поле в этой плоскости нам известно. Пусть его комплексная

амплитуда есть 70 , 0 , D 0 , , где функции 0 , и 0 , описывают распределение амплитуд и фаз колебаний

в плоскости 0. Что происходит с волной далее, по мере ее распространения в области & 0, как изменяется структура

волны — распределение амплитуд и фаз колебаний, что собой представляет световое колебание в некоторой точке наблюдения 6?

Согласно принципу Гюйгенса каждую точку , плоскости0, куда пришла волна (каждую малую площадку ), можно рассматривать как источник вторичной волны. То есть можно представить себе, что волна возбуждает колебания некоторого фиктивного источника, который и переизлучает вторичную волну. Френель дополнил принцип Гюйгенса, предложив расматривать световое колебание в любой точке наблюдения 6 в области& 0 как результат интерференции этих вторичных волн.

Какие свойства приписывает принцип Гюйгенса–Френеля фиктивным источникам и вторичным волнам, которые переизлучаются ими?

Поясним принцип Гюйгенса–Френеля, вернувшись к рассмотренной ранее задаче — дифракции на непрозрачном экране с отверстием (рис. 8.12 б). Маленькая площадка , расположенная в точке , на открытой части волнового фронта (т. е. в области отверстия), рассматривается как источник сфериче-

где — расстояние от источника до точки наблюдения 6, т. е. для вычисления вклада, который дает эта площадка в суммарное колебание, нужно учесть ослабление амплитуды (множитель 1 ) и набег фазы (множитель D ) как в сферической волне. При этом предполагается, что амплитуда излучения , площадки и ее начальная фаза , задаются амплитудой0 , и фазой 0 , колебания, созданного в точке , освещающей волной. Напомним, что, согласно принятым граничным условиям (8.2), на открытой части волнового фронта, т. е. в области отверстия, волна не искажается препятствием, причем работают лишь вторичные источники, находящиеся на открытой части, не затененной непрозрачным экраном.

ричных когерентно переизлучающих фиктивных источников внутри площадки. Наконец, предполагается, что амплитуда колебания в точке наблюдения пропорциональна видимой из

Полное световое колебание есть результат интерференции всех вторичных волн, т. е. волн, посылаемых всеми площадками

, расположенными в области отверстия:

где 0 — некоторый коэффициент пропорциональности, который еще подлежит определению, 7 6 — комплексная амплитуда в точке наблюдения 6. Формула (8.44) представляет собой количественную формулировку принципа Гюйгенса–Френеля, которую можно использовать для решения конкретных дифракционных задач.

8.7.Дифракция Френеля. Дифракционные задачи

сосевой симметрией

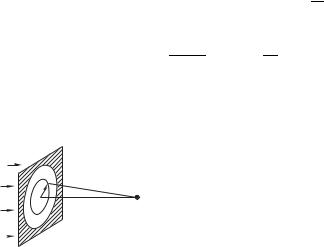
Круглое отверстие в непрозрачном экране. Применим принцип Гюйгенса–Френеля для нахождения светового колебания в точке наблюдения 6, находящейся на оси круглого отверстия в непрозрачном экране (рис. 8.13). Отверстие освещается плоской нормально падающей волной амплитуды 0.

Полагаем, что радиус отверстия 0 много меньше расстояния до точки наблюдения, поэтому множитель наклона в (8.44) можно считать близким к единице: # 1. Кроме того, при том же условии 0 амплитудный множитель 1 , учитывающий сферическую расходимость волн от вторичных источников, расположенных в области отверстия, можно считать приближенно одинаковым для всех вторичных источников и равным 1 1 . Тогда из (8.44), находим

Разумеется, расстояние в фазовом множителе D необходимо вычислить аккуратнее: ведь ошибка в определении на величину 2 приводит к ошибке в фазе колебания в точке наблюдения на величину $, что недопустимо (ошибки в фазах слагаемых колебаний должны быть малы в сравнении с $). Расстояние от некоторого вторичного источника , находящегося на расстоянии 3 от центра отверстия до точки 6, оценим так (рис. 8.13):

Нахождение суммарного колебания в точке наблюдения сводится к суммированию вкладов элементарных колечек. Разбив все отверстие на такие элементарные колечки одинаковой площади ; 2$3 3, мы приходим к задаче сложения колебаний одинаковой амплитуды 0, фазы которых растут пропорционально номеру кольца: 2 0. Сдвиг по фазе обусловлен тем, что каждое последующее колечко (б´ольшего радиуса) отстоит от точки наблюдения на большее расстояние и сдвиг по фазе связан с разностью расстояний : . Суммарное колебание

0D 2 в пределе, при 0 0 дает значение инте-

грала. Векторная диаграмма, которая и позволит нам вычислить интеграл (8.48) — это спираль Френеля (см. § 1.3).

рого равна амплитуде колебания, а его направление горизонтально (фаза колебания 2 0 0). Вклад -го колечка,

8.7 ] Дифракция Френеля 587

0 0) есть 0D 2 ; он изображается вектором той же длины 0 с углом наклона 2 0.

Мы получаем цепочку векторов, в которой каждый последующий вектор повернут относительно предыдущего на один и тот же угол 2 0 (рис. 8.14). Последний из изобра-

Он называется радиусом первой зоны Френеля (т. е. первая зона Френеля — круг радиуса 31). Разность фаз колебаний и1, равная $, означает, что расстояние 1 от края первой зоны Френеля до точки наблюдения 6 больше, чем расстояние от центра отверстия до точки 6 на 2: 1 2. Суммарный вклад первой зоны Френеля изображается вектором 1 — сум-

сдвинуто по фазе на 2$, т. е. синфазно с колебанием, созданным малой площадкой, расположенной в центре отверстия (вектор1 на рис. 8.14). Разности расстояний соответствует разность фаз 2$, т. е. 2 0 2$, откуда 0 2 , а радиус последнего колечка (которому отвечает последний вектор на диаграмме

рис. 8.15) равен 32 2 .

Кольцевая зона на отверстии между 31 и 32 называется второй зоной Френеля, 32 — это внешний радиус второй зоны

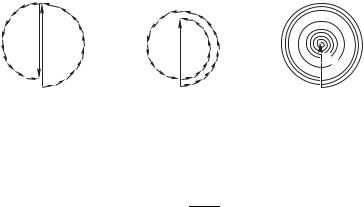
Френеля. Суммарный вклад второй зоны изображается вектором 2 (рис. 8.15), который антиколлинеарен вектору A1 на рис. 8.14, т. е. колебание, созданное в точке наблюдения второй зоной Френеля, противофазно колебанию от первой зоны. Если бы вклады всех элементарных колечек имели равную амплитуду, то амплитуды колебаний 1 и 2 были бы одинаковы и колебания первой и второй зон погасили бы друг друга полностью: 1 2 0. В действительности с ростом радиуса колечка амплитуда его вклада постепенно уменьшается: роль

при этом играет как постепенное, очень медленное уменьшение множителя наклона #, так и уменьшение амплитуды с ростом расстояния 1 . Итак, каждый элементарный вектор

вцепочке векторов на рис. 8.15 чуть меньше каждого вектора

вцепочке на рис. 8.14. Поэтому и суммарный вектор 2 чуть меньше вектора 1. Векторная диаграмма, изображающая вклад двух зон Френеля показана на рис. 8.16. Суммарный вклад двух зон хотя и чрезвычайно мал, но все же отличен от нуля. Итак, интенсивность света в точке 6 близка к нулю, если отверстие

содержит две зоны Френеля: 0 2 .

Пусть радиус отверстия постепенно увеличивается и, нако-

нец, становится равным 33 3 . Можно легко проверить, что край отверстия при этом отстоит от точки 6 на расстояние3 3 2, а колебание, созданное тонким колечком, примыкающим к краю, сдвинуто по фазе на величину 3$ по отношению

к колебанию от центрального элемента отверстия (т. е. эти колебания противофазны). 33 — это внешний радиус третьей зоны Френеля (кольцевой зоны между 32 и 33). Очевидно, суммарный

вклад третьей зоны 3 лишь чуть меньше по амплитуде вклада второй зоны. Векторная диаграмма, изображающая вклад трех зон Френеля представлена на рис. 8.17. Амплитуда суммарного колебания лишь немного меньше амплитуды 1 колебания, созданного отверстием в одну зону Френеля.

При дальнейшем увеличении радиуса отверстия «открываются» все новые и новые зоны Френеля: начинают «работать» все

новые и новые витки очень медленно скручивающейся спирали, которая показана на рис. 8.18 и называется спиралью Френеля.

Радиус -й зоны Френеля равен

Ясно, что если отверстие содержит четное число зон Френеля, то интенсивность света в точке наблюдения близка к нулю, а если нечетное, то интенсивность почти такая же, как и при отверстии в одну зону Френеля.

Конечно, с ростом радиуса отверстия «скручивание» спирали проявляется все сильнее и сильнее, множитель наклона #

уменьшается с ростом #, сказывается также увеличение расстояния между вторичными источниками, лежащими вблизи края отверстия и точкой 6 — все это приводит к уменьшению амплитуд колебаний от этих источников в точке наблюдения. Понятно, что если работают все зоны Френеля (т. е. непрозрачный экран отсутствует), то все витки спирали на рис. 8.18 дают свой вклад, а вектор 0, проведенный из начала спирали в ее фокус есть ни что иное, как амплитуда колебаний в точке 6 при отсутствии какого-либо препятствия на пути волны. Обратите внимание на удивительное обстоятельство: амплитуда колебаний в точке наблюдения при отсутствии препятствия на пути волны 0 вдвое меньше, чем амплитуда 1 колебания, созданного отверстием в одну зону Френеля: 0 1 2, а интенсивность вчетверо меньше: :0:1 1 4.

Построенная нами векторная диаграмма позволяет попутно определить константу 0 в формуле (8.44). Длину цепочки векторов, образующих дугу полуокружности на рис. 8.14, можно найти с помощью (8.49). Действительно, каждый элементарный вектор в цепочке имеет длину 0, а длина всей цепочки 0 ! 0. Согласно (8.49) она равна: 0 2$ . Радиус этой полуокружности представляет собой не что иное, как значение интеграла (8.48) при 0 (что соответствует ситуации, когда препятствие на пути волны отсутствует). Мы получаем

вектора, фазу которого мы приняли за нуль. Подставляя полученное значение в правую часть (8.47), а также учитывая,

Зонная пластинка Френеля. Поставим на пути плоской, нормально падающей волны прозрачную пластинку и фиксируем положение точки наблюдения 6 на расстоянии за пластинкой (рис. 8.19). Нарисуем на пластинке кольцевые зоны Френеля согласно формуле (8.51). Далее, все нечетные зоны Френеля (первую, третью, пятую и т. д.) оставим прозрачными, а все четные зоны (вторую, четвертую, шестую и т. д.) зачерним, сделав

590 Дифракция [ Гл. 8

их непрозрачными для света. Такая пластинка (с чередующимися прозрачными и непрозрачными зонами Френеля) называется

ния ориентации всех элементарных векторов, рис. 8.20). Мы видим, что вклады всех оставшихся нечетных зон 1, 3, 5, ...

изображаются коллинеарными векторами, т. е. колебания, созданные в точке наблюдения всеми нечетными зонами, оказываются синфазными. Амплитуда результирующего ко-

лебания A равна при этом сумме амплитуд слагае-

мых колебаний: 1 3 5 , а интенсивность : 2 1 3 5 2. Мы видим, что зонная пластинка Френеля обладает фокусирую-

щими свойствами, существенно увеличивая интенсив- ность света в точке 6, которая является точкой фо- кусировки зонной пластинки. Заметим, что размеры пластинки (ее радиус 0) обычно существенно мень- ше, чем расстояние до точки фокусировки, поэто- му вклады всех зон Френеля примерно равны по амплитуде и равны 1. Найдем выигрыш от фокусировки — отношение интенсивности света : в фо- Рис. 8.20

кусе зонной пластины к интенсивности света :0, падающего на пластинку (при отсутствии пластинки такая же интенсивность :0 была бы и в точке 6). Итак, число зон Френеля, укладывающихся на пластинке радиуса 0 найдем из условия:

нечетные). Каждая нечетная зона дает вклад, равный примерно1, поэтому суммарная амплитуда колебаний в точке 6 равна

: :0 4 106!

Подумайте, каким образом можно еще увеличить выигрыш от фокусировки, использовав вклады четных зон Френеля? Какова максимально возможная интенсивность в точке наблюдения, если