студ ивт 22 материалы к курсу физики / belonuchkin_ve_zaikin_da_tsipeniuk_ium_kurs_obshchei_fiziki

5.4 ] Теорема Пригожина 391

же количество тепла, что и отдает (при температуре 2 1), то выходит, что система отдает энтропию среде:

Иными словами, внутренняя структура, или самоорганизация, поддерживается за счет поглощения отрицательной энтропии. По предложению Бриллюэна отрицательная энтропия называется

негэнтропией.

Если говорить упрощенно, ячейки Бенара как бы в миниатюре воспроизводят условия, необходимые для существования жизни на Земле. Жизнь на Земле стала возможна лишь благодаря негэнтропии солнечного излучения. Жизнь на Земле — это упорядоченная структура, которая питается негэнтропией. Действительно, энергия солнечного излучения поступает на Землю из высокотемпературного источника (температура поверхности Солнца 1 6000 К), а уходит в космическое пространство при низкой температуре (температура Земли 2 300 K). Если предположить, что в среднем энергия на Земле не накапливается, то поток энтропии от Солнца на Землю будет меньше потока энтропии от Земли в космическое пространство. Полная аналогия с балансом энтропии в ячейках Бенара. Конечно, полнота аналогии ограничивается балансом энтропии. Анализ конкретных механизмов возникновения и эволюции живой материи выходят далеко за рамки термодинамики.

5.4. Теорема Пригожина

Как уже отмечалось, энтропия в определенном смысле слова управляет структурой открытой системы. В изолированной системе энтропия возрастает, система идет к равновесию. Если прирост энтропии внутри системы равен ее оттоку, возникает стационарное состояние или текущее равновесие, структура сохраняется. В самоорганизующихся системах энтропия убывает. Следовательно, значение энтропии служит мерой организации системы. Мы уже не раз отмечали, что для изолированной системы энтропия не может убывать. Обычно говорят о скорости возникновения энтропии

или сокращенно о производстве энтропии, записывая второе начало в виде

Процессы переноса характеризуются соответствующими потоками. Например, градиент температуры вызывает поток тепла, градиент плотности — поток массы и т. д. В общем случае

392 Неравновесные процессы [ Гл. 5

говорят, что потоки вызываются обобщенными термодинамическими силами (градиенты температуры или концентрации — простейшие примеры термодинамических сил). Таким образом, неравновесные системы характеризуются не только набором термодинамических параметров, но и скоростью их изменения во времени или в пространстве, определяющей потоки и термодинамические силы. Следует подчеркнуть, что обобщенные термодинамические силы не имеют ничего общего с силами в ньютоновском понимании этого слова. Введение понятия термодинамических сил позволяет описать в обобщенном виде поведение неравновесных систем.

Из опыта известно, что для широкого класса необратимых явлений и в широком диапазоне экспериментальных условий потоки являются линейными функциями термодинамических сил. Так закон Фурье связывает поток тепла с градиентом температуры, аналогичную форму имеет закон Фика, устанавливающий при диффузии линейную связь между потоком массы и градиентом концентрации. Наряду с этими «основными» (прямыми) процессами существуют и «побочные», перекрестные, которые неразрывно связаны с первыми. Например, перенос заряда под действием электрического поля, осуществляемый при движении ионов в электролите или электронов в металле, есть одновременно и перенос их кинетической энергии (тепла) и массы (диффузия). Наоборот, перенос массы под действием градиента плотности или тепла под действием градиента температуры в системе заряженных частиц есть одновременно и перенос заряда.

Все сказанное позволило американскому физику и химику Л. Онсагеру (1903–1976) предположить, что при небольших отклонениях от равновесия существует линейная связь между по-

Коэффициенты называются феноменологическими или кинетическими, и могут быть любыми функциями параметров состояния (температуры, давления, состава и т. д.). Однако они не зависят от и . Уравнения (5.6) американский физик К. Эккарт назвал термодинамическими уравнениями движения. Согласно принципу симметрии в уравнениях (5.6) недиагональные кинетические коэффициенты равны, т. е.

( ). Эти соотношения взаимности выведены Онсагером в 1931 г. Они являются следствием двух положений: принципа микроскопической обратимости (инвариантности механических уравнений движения по отношению к замене на ) и гипотезы о макроскопическом характере затухания флуктуаций (это

означает, что в среднем флуктуации рассасываются по обычным макроскопическим законам).

В термодинамике необратимых процессов принимается, что скорость приращения энтропии (производство энтропии) за счет необратимых процессов может быть представлена в виде

Это равенство является исходным для определения потоков и термодинамических сил. При малых отклонениях от равновесия происходящие в системе процессы должны удовлетворять соотношению (5.7).

Теперь мы можем перейти к одному из основных вопросов неравновесных систем. Нам хорошо известно, что равновесное состояние характеризуется максимумом энтропии. Возникает естественный вопрос: каким экстремальным свойством характеризуется стационарное неравновесное состояние? Иными словами, какая из функций состояния достигает экстремума (максимума или минимума) в стационарном неравновесном состоянии? Ответ на этот вопрос дает теорема Пригожина, согласно которой в стационарном неравновесном состоянии производство энтропии минимально. Производство энтропии в неравновесных системах с двумя обобщенными силами 1 и 2 выражается соотношением

В состоянии равновесия потоки и силы равны нулю, поэтому0. В неравновесном стационарном состоянии при фиксированной термодинамической силе 1 (фиксирована разность температур в прерывной системе или градиент температуры в непрерывной системе) поток 2, связанный с другой силой, обращается в нуль. Таким образом, из производства энтропии исчезает второй член, а первый член изменяется таким образом, что достигает минимума. Теорема о минимуме производства энтропии отражает внутреннюю устойчивость неравновесных систем.

Теорема Пригожина обладает большой общностью, она применима ко всем неравновесным стационарным состояниям независимо от конкретной природы системы. Математически условие устойчивости стационарных состояний с минимальным производством энтропии записывается в виде неравенства

Это неравенство означает, что внутренние неравновесные процессы всегда действуют в направлении, уменьшающем производство энтропии. Именно поэтому система, находящаяся в состоянии с минимальным производством энтропии не может самопро-

извольно из него выйти. Можно сказать это и другими словами: условие (5.9) указывает, в каком направлении развивается физическая система в процессе эволюции, и поэтому оно называется

критерием эволюции.

Наглядным примером сказанному служит деление клеток, рассматриваемых как открытые системы и моделируемых сферой радиуса . Если внутренняя структура клетки не изменяется, то производство энтропии внутри этой системы, обусловленное происходящими в клетке биохимическими процессами, пропорционально объему, отток — поверхности, прирост энтропии равен их разности. При некотором значении радиуса 0 производство энтропии уравновешивается ее оттоком, 0. Таким образом, поскольку производство энтропии пропорционально 3, а отток —2, то при 0 энтропия возрастает ( 0). Рост энтропии означает увеличение беспорядка, клетка погибнет, если не разделится на две части. При делении клетки суммарный объем не меняется, а поверхность увеличивается, поэтому энтропия уменьшается и тем самым поддерживается самоорганизация системы.

5.5. Периодические процессы в экологии и химии

Рассмотренные нами в § 5.3 ячейки Бенара — типичный пример возникновения упорядоченной пространственной структуры из хаотического состояния. Однако структуры могут образовываться и во времени (временные), существуют и пространствен- но-временные структуры.

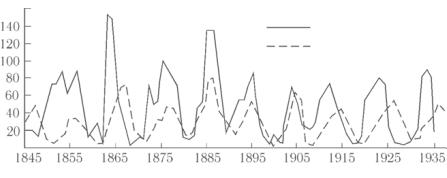
Примером временных периодических структур в живой природе может служить эволюция численности зайцев-беляков и рысей. На рис. 5.8 показано изменение числа рысей и зайцев-беля- ков, установленное по числу заготовленных шкурок, полученных компанией «Хадсон Бей» на протяжении 90 лет. Это типичный пример временных изменений в системе «хищники–жертвы».

N, 103

зайцы

ðûñè

t, ãîäû

Рис. 5.8

Количественные изменения популяции определяются многими факторами, однако для качественного объяснения временной корреляции на рис. 5.8 можно ограничиться одним наиболее существенным фактором. Рыси питаются зайцами, а зайцы поедают растительный корм. Возрастание числа зайцев приводит к росту запасов доступной пищи у рысей, поэтому они начинают интенсивно размножаться и их число увеличивается. На каком-то этапе рысей становится так много, что уничтожение зайцев происходит очень быстро. Число зайцев начинает медленно убывать, запасы пищи у рысей уменьшаются, и, соответственно уменьшается их численность. В результате число зайцев увеличивается. Рыси снова начинают размножаться, и все повторяется сначала.

Рассмотренный биологический пример известен в литературе под названием процесса «хищник-жертва», или процесса Лотки–Вольтерры. Модель Лотки–Вольтерры — модель борьбы за существование — описывается системой уравнений:

Здесь — число «жертв» (зайцы, караси), — число хищников (рыси, щуки), можно считать даже, что эти переменные соответствуют числу трудящихся и организованных преступников. Коэффициент описывает скорость естественного прироста зайцев в отсутствие рысей, — естественное вымирание рысей, лишенных зайцев. Вероятность взаимодействия зайцев и рысей (встречи жертв с хищниками) считается пропорциональной как числу зайцев, так и рысей (член ). Каждый акт взаимодействия уменьшает популяцию зайцев, но способствует увеличению числа рысей (члены и в правой части уравнений).

Эта модель описывает не только колебания популяций в экологии, она является также моделью незатухающих концентрационных колебаний в химических системах, о которых пойдет речь дальше. В науке часто встречается ситуация, когда разные явления математически описываются одинаково. В таких случаях говорят об изоморфизме уравнений и о структурном изоморфизме явлений.

Конечно, модель Лотки–Вольтерры является идеализацией, такой же, как, например, математический маятник без затухания. Однако от этого ее значение не уменьшается. С термодинамической точки зрения модель Лотки–Вольтерры интересна тем, что описываемый ею процесс занимает промежуточное значение между устойчивым стационарным состоянием с минимальным производством энтропии и периодическим процессом

с предельным циклом. Предельным циклом называется изолированная замкнутая траектория , обладающая тем свойством, что все другие траектории в ее окрестности являются спиралями, закручивающимися в направлении .

Пространство, в котором существует траектория , это в данном случае пространство концентраций или численностей популяций (фазовое пространство). Если концентрации или численность популяций зависят от времени, то, исключая время, можно найти связь между концентрациями. Геометрически эта связь изображается в виде траектории в фазовом пространстве, перемещение по которой соответствует эволюции системы во времени. Эта траектория является, как принято говорить, фазовым портретом системы. Как выглядит фазовый портрет системы в различных случаях, мы рассмотрим чуть позже в § 5.7. Сейчас мы лишь отметим, что если система находится в устойчивом стационарном состоянии, то произвольная флуктуация затухает

исистема со временем возвращается в первоначальное стационарное состояние (к своему предельному циклу), как это происходит в режиме теплопроводности на кривой 1 рис. 5.7.

Сточки зрения неравновесной термодинамики процесс Лотки–Вольтерры интересен тем, что происходит в системе, где нарушена связь потоков и сил. Термодинамическая сила — для реакций это химическое сродство — в схеме Лотки–Вольтерра равна бесконечности. Система как бы «бесконечно далеко удалена» от состояния равновесия. Вместе с тем система еще не перешла в неустойчивое состояние. На рис. 5.7 это состояние соответствует точке излома. Говорят о колебаниях на термодинамической ветви 1 в отличие от ветви 2, которая соответствует образованию новой структуры за границей устойчивости термодинамической ветви.

Много примеров образования пространственных, временных

ипространственно-временных´ структур дают нам и химические реакции. Одним из наиболее впечатляющих примеров существования временных´ структур в химии являются колебательные реакции, которые были впервые обнаружены в 1959 г. Б.П. Белоусовым (1893–1970). Его результаты были настолько неожиданными, что казались многим попросту невозможными

ипотому вначале не принимались к публикации в научных журналах.

Существенный прогресс в понимании механизма реакции начался с появлением работ А.М. Жаботинского (р. 1938). Классическим примером колебательной химической реакции служит реакция Белоусова–Жаботинского, наблюдавшаяся в растворе

серной кислоты (H2SO4), малоновой кислоты (CH2(COOH)2), сульфата церия (Ce2SO4) и бромида калия (KBrO3). Точнее, это целая совокупность реакций: в ее основе окислительно-восстано-

5.5 ] Периодические процессы в экологии и химии 397

вительная реакция ионов церия. Ход процесса определяется катализом превращения ионов церия Ce4 Ce3 в присутствии малоновой кислоты с образованием Br . Ион Br является ингибитором обратного процесса, он подавляет обратное превращение. В результате весь Ce4 превращается в Ce3 . Затем начинается обратная реакция, катализируемая одним из промежуточных продуктов реакции — BrO2 . Вновь образуется Ce4 , и все начинается снова. Период колебаний зависит от концентраций и находится в интервале от 2 до 100 с.

Чтобы следить за ходом реакции, в раствор добавляют индикатор (ферроин), который меняет свой цвет в зависимости от того, идет ли восстановительная или окислительная реакция. Когда происходит реакция Белоусова–Жаботинского, периодически меняется цвет раствора от красного (избыток Ce3 ) до синего (избыток Ce4 ). При определенных концентрациях после некоторого числа колебаний спонтанно возникают неоднородности концентрации и образуются устойчивые красные и синие слои, которые можно наблюдать примерно в течение 30 минут.

Реакция Белоусова–Жаботинского — это пример системы, функционирующей за границей устойчивости термодинамической ветви. Экспериментально было показано, что при одних

итех же условиях концентрационные колебания в реакции Белоусова–Жаботинского полностью воспроизводятся по амплитуде, форме и частоте. Это свидетельствует о том, что они соответствуют предельному циклу около неустойчивого стационарного состояния; неустойчивого, так как колебания рано или поздно прекращаются. Таким образом, из какого бы состояния ни началось движение, конечным состоянием будет всегда одна

ита же периодическая траектория в пространстве концентраций. Поэтому, в противоположность идущим в колебательном режиме химическим реакциям типа Лотки–Вольтерры, частота колебаний этих реакций является однозначной функцией макроскопических переменных, таких, как концентрация компонентов системы и ее температура. Течение химической реакции становится когерентным во времени. Таким образом, химическая реакция превращается в химические часы.

Процессы изменения концентрации вещества в системах, в которых происходят химические реакции, при некоторых условиях совершенно аналогичны колебательным процессам в нелинейных механических и электрических системах. Иначе говоря, можно найти химические системы, поведение которых сходно с поведением, например, скрипичной струны, по которой проводят смычком, или с поведением систем регулирования и т. д.

Сейчас известно много примеров автоволновых процессов в химически активных средах. Возможно и существование кон-

центрационных волн, исходящих из точечного источника. В таком случае в первоначально однородной среде спонтанно возникают периодические диссипативные структуры — химическая реакция осциллирует с периодом в несколько минут и наблюдаются цветные спирали, расходящиеся от одного или нескольких центров, как это видно из приведенной на рис. 5.9 фотографии концентрационных спиральных авто-

волн в химически активной среде.

Так как реакция идет в замкнутой системе, система в конце концов приходит в однородное равновесное состояние. Можно сказать, что химический «организм» умирает, задушенный избытком энтропии, которую нет возможности выбрасывать в окружающую среду.

Класс рассмотренных реакций интересен не только тем, что он представляет собой нетривиальное химическое явление, но и тем, что он служит удобной моделью для изучения колебательных и волновых процессов в активных средах. Сюда относятся периодические процессы клеточного метаболизма; волны активности в сердечной ткани и ткани мозга; процессы, происходящие на уровне экологических систем.

5.6. Возникновение хаоса в простой системе

Все наши интуитивные представления о хаотическом, случайном поведении связаны с действием внешних шумов или внутренних флуктуаций. Но в динамической системе ни шумов, ни флуктуаций нет, есть только полная детерминированность — алгоритм, который однозначно определяет поведение системы при заданных начальных условиях! Многие еще могли бы согласиться с тем, что хаотическая динамика возможна в очень сложных системах — системах с очень большим числом степеней свободы (например, для молекул в газе).

Обнаружение и понимание того факта, что хаотическое, случайное поведение возможно даже в очень простых динамических системах, явилось замечательным открытием современной науки. Сейчас эта проблема глубоко интересует гидродинамиков в связи с природой турбулентности, исследователей, прогнозирующих погоду, специалистов по химической кинетике и даже экономистов и социологов. Ведь с помощью теории динамических систем описываются самые разнообразные явления окружающего нас мира.

Рассмотрим два очень показательных эксперимента. Первый из них — колебания жидкого маятника. Поместим воду в тонкую кольцевую трубку, нижняя часть которой подогревается (пусть ее температура равна 1), а верхняя охлаждается и находится при температуре 2 1 (рис. 5.10). При достаточной разности тем-

ператур ( кр1 более легкая, нагретая в ос-

новании петли часть воды поднимется вверх, заставляя остывшую наверху воду опускаться вниз. Таким

образом вся жидкость, почти как твердое тело (поскольку все скорости здесь ничтожны по сравнению со скоростью звука, воду можно считать несжимаемой), будет вращаться внутри трубки. Эта механическая система очень проста — ее можно описать с помощью только трех переменных, зависящих от времени. Одна переменная характеризует скорость жидкости, и две — ее температуру. Как показывает эксперимент, жидкость в такой системе будет совершать очень простое движение — непрерывно вращаться по или против часовой стрелки.

Однако если подогревать воду снизу немного сильнее

кр2 кр1 , ситуация заметно усложнится: водяное кольцо внутри петли будет менять направление своего вращения, причем эта смена направлений оказывается случайной во времени, как это видно из рис. 5.10, где приведена зависимость разности температур между левой и правой вертикальными частями петли. Слева — конвективная петля, подогреваемая снизу, справа — зависимость разности температур между точками А и В от времени: при отсутствии конвекции (вверху), при стационарном вращении жидкости (в центре) и при случайном вращении то в одну, то в другую сторону (внизу).

Этот результат можно качественно пояснить следующим образом. Допустим, что в рассматриваемый момент времени жидкость движется по часовой стрелке. При достаточно большой разнице температур снизу и сверху петли (больше кр1) архимедова сила велика и водяное кольцо ускоряется настолько, что остывший вверху жидкий объем, проскочив горячее основание и не успев нагреться, уже не дотягивает до верха петли и приостанавливается (архимедова сила недостаточна, чтобы преодолеть силу вязкости и гравитацию). При этом опускающаяся (правая) часть жидкости теплее и, следовательно, легче поднимающейся. В результате торможения кольца жидкость в его основании нагревается и всплывает, но уже в противоположном направле-

400 Неравновесные процессы [ Гл. 5

нии — давление справа меньше, чем слева. Таким образом жидкость начинает раскручиваться против часовой стрелки. Затем все повторяется в обратном порядке. Как показывает эксперимент, при большой разности температур эти смены направлений оказываются случайными — величина нагрева единицы объема жидкости, скорость вращения кольца, его ускорение зависят от очень тонких деталей начального движения.

Теперь обратимся к несколько иному эксперименту, когда стохастические колебания возбуждаются с помощью внешней периодической силы. Рассмотрим поведение шарика в желобе с двумя минимумами при периодическом горизонтальном качании желоба (рис. 5.11). Когда амплитуда качаний

в каждой ямке уже случайно, а последовательность этих чисел оказывается совершенно нерегулярной и не содержит никаких закономерностей.

Естественно возникает вопрос, каким же образом в таких простых динамических системах при отсутствии всяких случайных сил движение оказалось случайным? Ведь движения детерминированной системы предопределены формулой ее поведения (алгоритмом), например дифференциальным (или каким-нибудь другим) уравнением. Ответ на этот вопрос, полученный физиками Н.С. Крыловым и М. Борном еще в 50-х годах, заключается в следующем: хаотичность поведения детерминированной системы определяется тем, что всякое (или почти всякое) ее движение неустойчиво. В таком случае даже малые изменения начального состояния приводят к сколь угодно сильному расхождению исходного и возмущенного движений (а это и есть неустойчивость), а значит, более поздние состояния системы фактически непредсказуемы, несмотря на полное знание закона движения.

Подчеркнем, что установившееся сложное хаотическое поведение детерминированной системы с неустойчивыми индивидуальными движениями никак не зависит от неточности задания начальных условий или статистики флуктуаций, приводящих в действие механизм неустойчивости. В этом смысле рассматриваемые системы являются не усилителями шума, а собственно генераторами хаоса. Например, в разобранном нами случае жидкого маятника даже при большой разности температур может, в принципе, существовать режим вращения в одну сто-