3865

на кривой, построенной на проверочном подмножестве. Однако на практике оказалось, что после прохождения этой точки сеть обучалась только посторонним шумам, содержащимся в обучающей выборке. Поэтому было принято решение об использовании точки минимума кривой тестирования в качестве критерия останова сеанса обучения. Когда ошибки на подмножествах оценивания и проверки не одинаково стремились к нулю(что характерно для данных не содержвщих шума), емкости сети оказывалось не достаточно для точного функционирования модели. В этом случае минимизировалась интегрированная квадратичная ошибка, что (приблизительно) эквивалентно минимизации обычной глобальной среднеквадратической ошибки при равномерном распределении входного сигнала.

Для повышения эффективности обучения ИНС использовалось комбинирование последовательного и пакетного режимов обучения. В рамках последовательного режима обучения корректировка весов проводилась после подачи каждого примера. Для примера рассмотрим эпоху, состоящую из N обучающих примеров, упорядоченных следующим образом: ((x1),d(1)),.., (x(N),d(N)). Сети предъявлялся первый пример(x(l),d(l)) этой эпохи, после чего выполнялись описанные выше прямые и обратные вычисления. В результате проводилась корректировка синаптических весов и уровней порогов в сети. После этого сети предъявлялась вторая пара (x(2),d(2)) в эпохе, повторялись прямой и обратный проходы, приводящие к поледующей коррекции синаптических весов и уровня порога. Этот процесс повторялся, пока сеть не завершала обработку последнего примера (пары) данной эпохи - (x(N), d(N)). В пакетном режиме обучения корректировка весов проводилась после подачи в сеть всех примеров обучения (всей эпохи). Для каждой эпохи функция стоимости определялась как среднеквадратическая ошибка, представленная в составной форме

где сигнал ошибки ej (n) соответствует нейрону j для примера обучения n. Ошибка ej (n) равна разности между dj(n) и уj(n) для j-гo элемента вектора желаемых откликов d(n) и соответствующего выходного нейрона сети. В выражении (3.36) внутреннее суммирование по j выполняется по всем нейронам выходного слоя сети, в то время как внешнее суммирование поп выполняется по всем образам данной эпохи. При заданном параметре скорости обученияh

корректировка, применяемая к синаптическому весу w ji связывающему нейроны i и j, определялась следующим дельта-правилом

Согласно (3.38) в пакетном режиме корректировка веса Dwji (n) выполняется только после прохождения по сети всего множества примеров.

121

Процесс комбинирования данных режимов обучения состоял в следующем. В случае наличия избыточных данных использовался последовательный режим обучения. Его применение позволяло использовать меньший объем внутреннего хранилища для каждой синаптической связи. Более того, путем предъявления обучающих примеров в случайном порядке(в процессе последовательной корректировки весов) достигался стохастический поиск в пространстве весов. Это, в свою очередь, сокращало до минимума возможность остановки алгоритма в точках локальных минимумов. Во всех остальных случаях использовался пакетный режим обучения. Он обеспечивал более точную оценку вектора градиента при «обедненных» данных и позволял распараллелить вычисления.

Для обоснования критерия прекращения(останова) обучения рассматривались уникальные свойства локального и глобального минимумов поверхности ошибок. Обозначим символом w вектор весов, обеспечивающий минимум, будь то локальный или глобальный. Необходимым условием минимума является достижение вектора градиента g(w) (т.е. вектора частных производных первого порядка) для поверхности ошибок в точке нулевых значений. На практике это означает, что алгоритм обратного распространения ошибок сошелся, если евклидова норма вектора градиента достигла достаточно малых значений. Недостатком этого критерия сходимости является то, что для сходимости обучения может потребоваться довольно много времени. Кроме того, необходимо постоянно вычислять вектор градиентаg(w). Другим уникальным свойством минимума является то, что функция стоимости (или мера ошибки) Eav (w) в точке w = w* стабилизируется. Отсюда можно вывести еще один критерий сходимости. Критерием сходимости алгоритма обратного распространения ошибок является достаточно малая абсолютная интенсивность изменений среднеквадратической ошибки в течение эпохи. Практические результаты показали, что интенсивность изменения среднеквадратической ошибки можно считать достаточно малой, если она лежит в пределах от0,1-1 % за эпоху. В процессе функ-

ционирования алгоритма обратного распространения ошибок использовался еще один критерий сходимости. После каждой итерации обучения сеть тестировалась на эффективность обобщения. Процесс обучения останавливался, когда эффективность обобщения становилась удовлетворительной или когда оказывалось, что пик эффективности уже пройден.

Блок-схема алгоритма обратного распространения ошибок представлена на рис. 3.13. Блоки 1,10 используются для пуска и остановки алгоритма обратного

распространения ошибок.

В блоке 2 реализован ввод исходных данных, таких как:

- элементы обучающей выборки (как правило, они должны быть нормализованы);

- значения весов (начальные значения весов могут быть случайными или детерминированными);

- вектор выходных значений сигналов.

122

1

Начало

2

Ввод исходных данных

3

Определение

выходного

сигнала

4

Определение функционала квадратичной ошибки

5

Определение производных сигналов ошибок обратного распространения

6

Фиксация знака производной

8

Генерация приращений весов

Рис. 3.13. Блок-схема алгоритма обратного распространения ошибок

123

Блок 3 обеспечивает расчет выходного сигнала.

В блоке 4 рассчитывается значение среднеквадратичной ошибки.

Блок 5 реализует определение производных сложной функции (сигнала и функции активации).

В блоке 6 фиксируется значение производной.

Блок 7 обеспечивает проверку изменения знака производной. Если он не изменился, то управление передается в блок 9. В противном случае управление передается в блок 8.

Блок 9 вывод результатов. В качестве результатов выступает набор весовых коэффициентов при которых достигается значение минимума функции ошибки.

Ниже приведен фрагмент программного кода, реализующий алгоритм обратного распространения ошибок:

procedure TNSet.MTeach; var

i, //слой

j, //нейрон k:Integer; // вход xsum:Double;

begin

//формирование массива ошибок // расчет фактических ошибок нейронов выходного слоя

for j:=1 to fConfig[LayerCount-1] do Osh[LayerCount-1,j]:=(outputm[LayerCount-1,j]-

inputm[LayerCount,j])*Posh[LayerCount-1,j]; //расчет суммарной ошибки

xsum:=0;

for j:=1 to fConfig[LayerCount-1] do xsum:=xsum+Osh[LayerCount-1,j]; Sosh:=xsum/fConfig[LayerCount-1];

//расчет фактических ошибок нейронов скрытых слоев приращений весов и новых весов

//начинаем от предпоследнего (последний скрытый) до 1-го for i:=LayerCount-2 downto 1 do

for j:=1 to fConfig[i] do begin

xsum:=0;

for k:=0 to fConfig[i+1] do xsum:=xsum+Osh[i+1,j]*w[i,j,k];

Osh[i,j]:=xsum*Posh[i,j];

//Osh[i,j]:=xsum*outputm[i,j]*(1-outputm[i,j]);

//находим приращение веса и новое значение веса

124

for k:=0 to fConfig[i+1] do begin

//WT[i,j,k]:=-Osh[i+1,j]*fMiu*outputm[i,j]; WT[i,j,k]:=-Osh[i+1,j]*fTS*outputm[i,j]+fMiu*WT[i,j,k];

w[i,j,k]:=w[i,j,k]+WT[i,j,k];

end;

end;

end;

Вкачестве альтернативного метода обучения ИНС использован«Алгоритм имитации отжига», который реализует одноименный алгоритм в интересах оптимизации поиска глобального экстремума целевой функции. Метод имитации отжига представляет собой алгоритмический аналог физического процесса управляемого охлаждения. Предложенный Н. Метрополисом в 1953 г.

[55]и доработанный многочисленными последователями, он в настоящее время считается одним из немногих алгоритмов, позволяющих оперативно находить глобальный минимум функции нескольких переменных. Метод имитаций отжига основан на идее, заимствованной из статической механики. Он отражает поведение материального тела при отвердевании с применением процедуры отжига. Для получения качественного материала из расплава при отвердевании его температура должна уменьшаться постепенно, вплоть до момента полной кристаллизации. Если процесс остывания протекает слишком быстро, образуются значительные нерегулярности структуры материала, которые вызывают внутренние напряжения. В результате общее энергетическое состояние тела, зависящее от его внутренней напряженности, остается на гораздо более высоком уровне, чем при медленном охлаждении. Быстрая фиксация энергетического состояния тела на уровне выше нормального аналогична сходимости оптимизационного алгоритма к точке локального минимума. Энергия состояния тела соответствует целевой функции, а абсолютный минимум этой энергии – глобальному минимуму. В процессе медленного управляемого охлаждения, называемого отжигом, кристаллизация тела сопровождается глобальным уменьшением его энергии, однако допускаются ситуации, в которых она может на ка- кое-то время возрастать (в частности, при подогреве тела для предотвращения слишком быстрого его остывания). Благодаря допустимости кратковременного

повышения энергетического уровня возможен выход из ловушек локальных минимумов, которые возникают при реализации процесса. Только понижение температуры тела до абсолютного нуля делает невозможным какое-либо самостоятельное повышение его энергетического уровня. В этом случае любые внутренние изменения ведут только к уменьшению общей энергии тела.

Вреальных процессах кристаллизации твердых тел температура понижается ступенчатым образом. На каждом уровне она какое-то время поддерживается постоянной, что необходимо для обеспечения термического равновесия. На протяжении всего периода, когда температура остается выше абсолютного

125

нуля, она может как понижаться, так и повышаться. За счет удержания температуры процесса поблизости от значения, соответствующего непрерывно снижающемуся уровню термического равновесия, удаётся обходить ловушки локальных минимумов, что при достижении нулевой температуры позволяет получить и минимальный энергетический уровень [173].

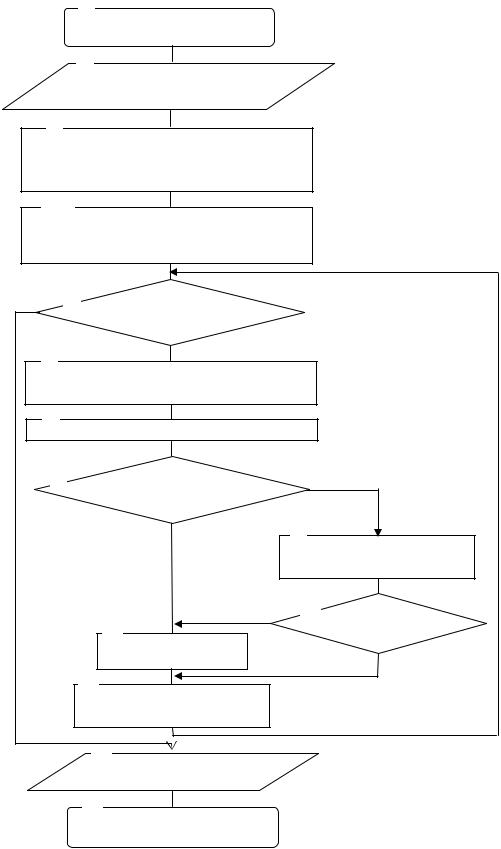
Блок-схема алгоритма имитации отжига, который использовался для обучения многослойного персептрона приведен на рис. 3.14.

Блоки 1, 14 используются для пуска и остановки алгоритма.

Вблоке 2 реализован ввод исходных данных, таких как: значения входных параметров и соответствующего им отклика ИНС из обучающей или тестирующей выборок либо реальных данных.

Блок 3 обеспечивает генерацию начальных значений весов нейронных связей и температуры Tmax.

Вблоке 4 рассчитывается значение энергии в соответствии с соотноше-

нием E=(Y1 -Y1¢)2 +(Y2 -Y2¢)2 +(Y3 -Y3¢)2 +...+(Yn -Yn¢)2 .

Вблоке 5 реализована проверка условия наличия положительной температуры тела. Если данное условие выполнено, то управление передается в блок 6, в противном случае вычислительный процесс завершается и управление передается в блок 13.

Блок 6 обеспечивает генерацию значений приращений весов w’.

Вблоке 7 рассчитывается обновленное значение энергии E’.

Блок 8 предназначен для проверки условия превышения предыдущего значения энергии над текущим значением. Если данное условие выполняется, то управление передается в блок 11, в противном случае управление передается в блок 9.

В Блоке 9 реализована генерация случайных чисел в диапазоне от 0 до 1. Блок 10 предназначен для проверки условияexp(- D 2/T2)>R. Если данное

условие выполняется, то управление передается в блок11. В противном случае управление передается в блок 12.

Вблоке 11 весам присваиваются новые значения. Блок 12 обеспечивает снижение температуры.

Вблоке 13 осуществляется вывод полученных результатов– оптимальных значений весов ИНС.

Вданном алгоритме обучения реализован стохастически управляемый метод повторных рестартов. Для оценки его эффективности был проведен сравнительный анализ функционирования данного алгоритма, генетического алгоритма и алгоритма прямого перебора.

На рис. 3.15 приведена экранная форма интерфейса пользователя при исследовании данных алгоритмов обучения ИНС.

Окно имеет блочную структуру. В верхней части окна располагаются блоки заданий параметров трех алгоритмов обучения(генетического, имитации отжига и прямого перебора). Кроме того, в каждом блоке имеется окно, в котором отображается время выполнения соответствующего алгоритма обучения, а также кнопка его запуска – «Старт».

126

14

Конец

Рис. 3.14. Блок-схема алгоритма имитации отжига

127

Рис. 3.15. Экранная форма интерфейса исследования алгоритмов обучения ИНС

В нижней левой части экранной формы находится компонент задания обучающих примеров. В нижней правой части экранной формы находится таблица, в которой отображаются значения весов нейронных связей и ошибки соответствующих ИНС. В центре экранной формы имеется окно задания параметра α. Данный параметр определяет крутизну функции активации. При

a ®¥ функция вырождается в пороговую.

При a ® 0 функция активации становится линейной функцией с пороговым значением - 0,5. При a ® 1 данная функция является плавной сигмоидальной функцией (вариант, представляющий интерес в данной работе).

В табл.3.3 и 3.4 приведены экспериментальные значения основных параметров функционирования (времени работы и значения ошибок) для трех алгоритмов обучения.

В таблице 3.3 приведены результаты работы двух алгоритмов обучения, при постоянных исходных данных. В таблице 3.4 представлены результаты функционирования алгоритма прямого перебора для 5 вариантов исходных данных:

1.Max значение веса – 1, Min значение веса – -1, Шаг – 0,2;

2.Max значение веса – 1, Min значение веса – -1, Шаг – 0,1;

3.Max значение веса – 2, Min значение веса – -2, Шаг – 0,2;

4.Max значение веса – 2, Min значение веса – -2, Шаг – 0,1;

5.Max значение веса – 3, Min значение веса – -3, Шаг – 0,2.

128

Таблица 3.3 Результаты работы генетического алгоритма и алгоритма имитации отжига

Анализ полученных результатов показывает, что алгоритм имитации отжига является наиболее оперативным, но не самым точным из рассматриваемых методов обучения. Более высокую точность показал генетический алгоритм, но он затрачивает намного больше времени на работу чем алгоритм имитации отжига. Теоретически алгоритм прямого перебора является самым точным методом поиска глобального минимума функции. Однако на практике, по причине недостаточной аппаратной мощности ПК, оказалось невозможным получить значение глобального минимума за приемлемое время.

Модуль «Генетический алгоритм» реализует случайный поиск экстремума функции для нескольких аргументов. Он представляет собой симбиоз переборного и градиентного методов. Его основу составляет естественный отборглавный механизм эволюции [25, 29, 57]. В нем реализуются генетические коды индивидуумов – ДНК (дезоксирибонуклеиновая кислота), приспособленность индивидуумов, хромосомы, скрещивание, мутации и др. Детальное описание генетического алгоритма приведено в разделе 2.5.

Большое значение для обучения ИНС имеет ее архитектура. Рассмотрим последовательность процесса обучения сети в плоскости поиска ее оптимальной архитектуры. Обучение ведется путем минимизации целевой функцииE(w), определяемой только на обучающем подмножестве L. При этом значение целевой функции определяется как

где р - количество обучающих пар(хk, dk), yk - вектор реакции сети на возбуждение хk.

129

Минимизация функции (3.39) обеспечивает достаточное соответствие выходных сигналов сети ожидаемым значениям из обучающих выборок.

Цель обучения состоит в таком подборе архитектуры и параметров сети, которые обеспечат минимальную погрешность распознавания тестового подмножества данных, не участвовавших в обучении. Эту погрешность будем называть погрешностью обобщения EG(w). Co статистической точки зрения погрешность обобщения зависит от уровня погрешности обученияEL(w) и от доверительного интервала e . Она характеризуется неравенством:

Установлено [177], что значение e функционально зависит от уровня погрешности обучения EL(w) и от отношения количества обучающих выборок р к фактическому значению h параметра, называемого мерой ВапникаЧервоненкиса (МВЧ) и обозначаемого VCd. Данная мера отражает уровень сложности нейронной сети и тесно связана с количеством содержащихся в ней весов. Значение e уменьшается по мере возрастания отношения количества обучающих выборок к уровню сложности сети. Значение МВЧ функционально зависит от количества синаптических весов, связывающих нейроны между собой. Чем больше количество различных весов, тем больше сложность сети и соответственно значение меры VCd. Верхняя и нижняя границы МВЧ определяются в соответствии с неравенством:

где [ ] - целая часть числа, N — размерность входного вектора, К-количество нейронов скрытого слоя, Nw — общее количество весов сети, a Nn -общее количество нейронов сети.

Из выражения (3.41) следует, что нижняя граница диапазона приблизительно равна количеству весов, связывающих входной и скрытый слои, тогда как верхняя граница превышает двукратное суммарное количество всех весов сети. В связи с невозможностью точного определения меры VCd в качестве ее приближенного значения используется общее количество весов нейронной сети [174].

Таким образом, на погрешность обобщения оказывает влияние отношение числа обучающих выборок к количеству весов сети. Небольшой объем обучающего подмножества при фиксированном количестве весов вызывает хорошую адаптацию сети к его элементам, однако не усиливает способности к обобщению, так как в процессе обучения наблюдается относительное превышение числа подбираемых параметров(весов) над количеством пар фактических и ожидаемых выходных сигналов сети. Эти параметры адаптируются с чрезмерной (а вследствие превышения числа параметров над объемом обучающего множества - и неконтролируемой) точностью к значениям конкретных выборок, а не к диапазонам, которые эти выборки должны представлять. Фактически задача аппроксимации подменяется в этом случае задачей приближен-

130