
3479
.pdf
структур схожи по форме, ограничимся лишь подробным анализом дифракции волны на вспомогательной структуре.
H
x
R2+t
П
εr
R2
0 W |
d |
z |
-H2
 -h2
-h2
Рис. 2.21. Двухпазовая гребѐнка с диэлектрическим слоем (наклонное падение H-поляризованной волны)
Для однородной Е-поляризованной плоской волны, падающей в плоскости x0у на вспомогательную структуру (отсчет угла падения  показан на рис. 2.20), проекции векторов напряженностей электрического и магнитного полей падающей волны в области x > R1 + t записываются в виде
показан на рис. 2.20), проекции векторов напряженностей электрического и магнитного полей падающей волны в области x > R1 + t записываются в виде
Ezn |
e j n (x R1 t) e j 0 y , |
|
|
|
|||||
H yn |
0 |
|
e |
j 0 (x R1 |
t) |
e j |
0 y . |
(2.41) |
|
|
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Поле рассеянных волн (поле дифракции) в этой же области представляется совокупностью пространственных гармоник, описываемой рядом Фурье:
|
Ezp |
a n e j n (x R1 t) e j n y , |
||||
|
|
n |
|
|
|
(2.42) |
|
|
|
|
|
|
|
|
H yp |
a n |
n |
|
e n (x R1 |
t) e j n y , |
|
|
0 |
||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
где an |
неизвестные комплексные амплитуды ПГ; |
|||||
n=2 |
n/d+k0sin( ), |
0=( k20- |
2n)1/2 постоянные распространения n-й ПГ |
|||
вдоль оси 0y и оси 0x соответственно. |
|
|
|
|||
В областях R1+t > x > R1 |
(ПДВ) и R1 |
> x > 0 (прицельный зазор) |
||||
рассеянные поля представляются в виде соотношений, аналогичных (2.2). Поэтому приведем лишь записи для Е-компонент полей в этих областях:

E(zПДВр |
) |
(bn |
e |
j |
n (x |
R1 ) |
cn |
e j |
n (x |
R1 ) ) e j n y , |
|
(2.43) |
|||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E(zзазорр ) |
(fn |
e |
j |
n x |
gn |
e j |
n x ) |
e j n |
|
y , |
|
|
|
|
(2.44) |
||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где bn, cn, fn, gn неизвестные комплексные амплитуды ПГ; |
|
|
|
|
|||||||||||||
n=( k 22 - |
2n)1/2 |
поперечная постоянная распространения n-й ПГ в области |
|||||||||||||||
ПДВ в направлении оси 0x: k2=( 0 |
r 0 |
2)1/2. |
|
|
|
|
|
|
|
|
|
||||||
В пазах решетки поле представлено совокупностью волноводных мод: |
|||||||||||||||||
в области 0 > x > -h1; W > y > 0: |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
E(zpосн) |
|
|
dm1 |
sin(qm1 |
(x |
h1)) sin |
|
m |
y |
; |
(2.45) |
||||
|
|
|
|
|
W |
|
|
||||||||||
|
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в области 0 > x > -H1; d > y > W: |
|
|
|
|
|
|
|
|
|
|
|||||||
E(zpвсп) |
dm2 |
sin(qm2 |
(x |
H1)) sin |
|
m |
(y |
W) |
, |
(2.46) |
|||||||
|
d |
W |
|
|
|||||||||||||
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где dm1 и dm2 - неизвестные комплексные амплитуды волноводных мод; qm1=(k02 r1-( m/W)2)1/2 и qm2=(k02 r2-( m/(d-W))2)1/2 - постоянные
распространения волноводных мод основного и вспомогательного пазов вдоль оси 0x.
Hy -компоненты полей дифракции в рассматриваемых частичных областях находятся в соответствии с уравнениями Максвелла.
Сшивание тангенциальных компонент полей на границах раздела частичных областей x = 0, x = R, x = R+t приводит к системе функциональных уравнений относительно неизвестных комплексных амплитуд ПГ an, bn, cn, fn, gn, dm1, dm2:

a n |
0 |
bn |
e |
j n t |
cn |
e |
j |
n t |
, |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||
n |
a n |
0 |
0 |
n ( bn e |
j |
n t |
cn |
e |
j |
n t |
), |
|||
n |
|
|
|
|
|
|||||||||
bn cn |
|
fn e j n R1 |
gn e j n R1 , |
|
|
|
|
|
|
|
|
|
|
|
|||
n ( bn |
cn ) |
n ( fn e j n R1 gn e j n R1 ), |
|
|
|
|
|
|
|
|
|
||||||
(fn |
gn )e j |
n y |
|
dm1 sin qm1h1 sin |
|
m y |
, 0 |
|
y |
W, |
|
|
(2.47) |
||||
|
|
|
W |
|
|
||||||||||||
n |
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n |
( |
fn gn )e j |
n y |
j |
dm1qm1 cos qm1h1 |
sin |
|
|
|
m y |
|
, 0 |
y |
W, |
|||
|
|
|
|
W |
|||||||||||||
n |
|
|
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(fn |
gn )e j |
n y |
|
dm2 sin qm2H1 sin |
|
m (y |
W) |
, W |
y |
d, |
|
||||||
|
|
|
d |
W |
|
|
|
|
|||||||||
n |
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n |
( |
fn gn )e j |
n y |
j |
dm2qm2 cos qm2H1 sin |
|
m (y |
W) |
, W y d. |
||||||||
|
|
d |
W |
|
|||||||||||||
n |
|
|
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Разложив функции sin( my/W) и sin( m(y-W)/(d-W)) по полной ортогональной на периоде системе функций exp(j ny) и исключив из полученных уравнений неизвестные амплитудные коэффициенты bn, cn, fn, gn, получим парную систему линейных алгебраических уравнений 1-го рода бесконечного порядка относительно комплексных амплитуд в области x > R + t и волноводных мод dm1 и dm2 в пазах гребенки.
Для построения эффективного вычислительного алгоритма решения полученной СЛАУ использована операция регуляризации в соответствии с обобщенным правилом Миттры (2.7) – правилом редуцирования бесконечных парных СЛАУ. Она заключается в строго определенном выборе числа учтенных ПГ и волноводных мод в основном и вспомогательном пазах гребенки – величин L, M1 и M2 соответственно, и вытекает из требования удовлетворения искомого решения условию Мейкснера, определяющему поведение поля вблизи сингулярностей (ребер решетки).
Указанная операция регуляризации состоит в том, что при общем числе L учитываемых гармоник в области x R1 + t число волноводных мод M1 и M2 выбираются с учетом условия
lim |
M1 |
W d |
. |
(2.48) |
|
||||
L |
M2 |
1 W d |
|
|
Учитывая, что M1+M2=L, редуцированная СЛАУ запишется в следующем виде

|
M1 |
|
M 2 |
|
|
|
a n rn |
dm1 sin(qm1h1)pnm1 |
dm2 sin(qm2h 2 )pnm2 |
01, |
|
||
|
m 1 |
|
m 1 |
|
|
(2.49) |
|
M1 |
|
|
M 2 |
|
|
n a nsn |
jqm1dm1 cos(qm1h1)pnm1 |
jqm2dm2 cos(qm2h 2 ) pnm2 |
0 02, |
|||
|
m 1 |
|
|
m 1 |
|
|
где
rn |
exp( j |
n |
) / zn1 |
|
zn5 |
(1 |
exp( j2 |
n |
) zn 2 / zn1 ); |
|
|
||||||||||
zn5 |
( |
|
n |
|
n |
|
zn3 / zn 4 ) exp( j n |
)(zn 4 |
zn3zn 2 / zn1 ) |
n ; |
|
||||||||||
zn1 |
( |
n |
|
|
n )(exp( j |
n t) |
|
exp( |
|
j |
n t)) /(2 |
n ) |
exp( |
j |
n t); |
||||||
zn 2 |
( |
|
n |
|
n )(exp( j |
n t) |
|
exp( |
j |
n t)) /(2 |
n ) |
exp( |
j |
n t); |
|||||||
zn3 |
( |
|
n |
|
n )(exp( j |
n t) |
|
exp( |
j |
n t)) /(2 |
n ) |
exp( |
j |
n t); |
|||||||
zn 4 |
|
( n |
|
|
n )(exp( j |
n t) |
|
exp( |
|
j |
n t)) /(2 n ) |
exp( |
j |
n t); |
|||||||
sn |
exp( j |
n |
) / zn1 |
|
zn5 |
(1 |
exp( j2 |
n |
) zn 2 / zn1 ); |
|
|
||||||||||
01 |
exp( j |
0 |
) / z01 |
z06 |
|
z010 ; |
|
|
|
|
|
|
|
|
|||||||
02 |
exp( j |
0 |
) / z01 |
z07 |
|
z010 ; |
|
|
|
|
|
|
|
|
|||||||
z06 |
1 |
|
exp( j2 |
0 |
) |
z02 / z01; |
|
|
|
|
|
|
|
|
|||||||
z07 |
1 |
|
exp( j2 |
0 |
) |
z02 / z01; |
|
|
|
|
|
|
|
|
|||||||
z010 |
( |
0 |
|
0z03 / z01 ) / |
0 |
exp( j |
|
0 |
)(z04 |
z03 |
z02 / z01 ); |
||||||||||
pnm1 |
W |
|
m(1 |
( |
1)m e |
j |
n W ) |
; |
|
|
|
|
|
|
|||||||
|
d |
( |
|
m)2 |
( n |
|
W)2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
pnm2 |
(d W) |
m(e j |
n W |
( |
1)m e |
j n W ) |
. |
d ( |
m)2 |
( n |
(d |
W))2 |
|
||
|
|
|
Регуляризованная система уравнений (2.49) использована для построения алгоритма численного решения задачи и его программной реализации.
Анализ дифракции на структуре, изображенной на рис. 2.21, однородной плоской электромагнитной волны с Н-поляризацией выполняется аналогично приведенному выше; основное отличие состоит в представлении рассеянного поля в пазах решетки с помощью функций cos(qm1x) и cos(qm2x), cos( my/W) и cos( m(y-W)/(d-W)) для выполнения граничных условий на дне пазов и на ребрах решетки, а в соответствующих суммах по m дополнительно учтена волноводная мода с нулевым индексом (это обусловлено наличием в пазах при Н-поляризации Т-волны). Структуры парных систем граничных уравнений в случаях E- и H-поляризации аналогичны.

На рис. 2.22 представлены расчетные зависимости относительной |
||||||||||
энергии P0 зеркально отраженной волны от отношения периода ДР к длине |
||||||||||
волны в свободном пространстве |
d / |
0 |
при дифракции E-поляризованной |
|||||||
волны на одномерно-периодичной гребенке без диэлектрика. |
|
|||||||||
|
1 Р10 |
|
|
|
|
|
|
|
|
|
|
|
0 .9 |
|
|
|
|
|
|
|
|
|
|
0 .8 |
|
|
|
|
|
|
|
|
|
|
0 .7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
v y |
0 .6 |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y( x ) |
|
|
|
|
|
|
|
|
|
|
v y1 i |
0 .5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 1( x ) |
0 .4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
0 .3 |
|
|
|
|
|
|
|
|
|
|
0 .2 |
|
|
|
|
|
|
|
|
|
|
0 .1 |
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
1 .25 |
1 .5 |
1 .75 |
2 |
2 .25 |
2 .5 |
2 .75 |
|
|
|
|
|
|
xi |
|
|
|
æ |
|
|
|
1 |
|
|
X |
|
|
2 .75 |
|
|
Рис. 2.22. Расчетные зависимости относительной энергии P0 |
||||||||||
зеркально |
отраженной |
|
волны |
с |
Е-поляризацией |
от |
||||
нормированного частотного параметра (зависимость 1 взята из |
||||||||||
литературы; кривая 2 получена авторами) |
|
|
|
|||||||
Параметры ДР были выбраны следующими: H1=0, =h1/d=0.25, u=W/d=0.8. Зависимость 1 получена методом полуобращения. Кривая 2 - результат метода редуцирования СЛАУ при общем числе учитываемых гармоник N=9. Расчеты показывают, что при редуцировании СЛАУ по правилу (2.7) среднеквадратическое отклонение (СКО) приближенного решения от строгого не превышает 7 %, причем кривая 2, полученная численным методом, в широком частотном диапазоне повторяет поведение зависимости, полученной полуаналитическим методом, включая точку, в которой производная функции P0=P0( ) терпит разрыв.
На рис. 2.23 изображены кривые, соответствующие случаю H-поляризации.

1 Р10 |
|
|
|
|
|
|
|
||
|
0 |
.9 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
.8 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
0 |
.7 |
|
|
|
|
|
|
|
v yi |
0 .6 |
|
|
|
|
|
|
|
|
y( x ) |
|
|
|
|
|
|
|
|
|
v y1 i |
0 |
.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 1( x ) |
0 .4 |
|
|
|
|
|
|
|
|
|
0 .3 |
|
|
|
|
|
|
|
|
|
0 .2 |
|
|
|
|
|
|
|
|
|
0 .1 |
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
1 |
1 .25 |
1 .5 |
1 .75 |
2 |
2 .25 |
2 .5 |
2 .75 |
|
|
|
|
|
|
|
|
|
æ |
1 x X 2 .75
Рис. 2.23. Расчетные зависимости относительнойi энергии зеркально отраженной волны Н-поляризации от частотного параметра
Параметры ДР оставлены прежними, волна падает нормально. Общее число учтенных гармоник N=7. Обозначения кривых на рис. 2.23 соответствуют принятым на рис. 2.22. Из рис. 2.23 следует, что при правильно выполненном усечении СКО не превышает 3 %. Численный анализ, проведенный с учетом 15 гармоник, показывает, что для случаев E- и H-поляризованных падающих волн СКО не превышает 2 % (относительно результатов, полученных методом полуобращения).
Сходимость метода редуцирования парных СЛАУ проверяется математическим моделированием дифракции плоской Н-поляризованной электромагнитной волны на одномерно-периодичной гребенке со слоем диэлектрика, в частности, анализом угло-частотных характеристик структуры и зависимости постоянной вытекания (-1)-й поверхностной гармоники от частоты падающей волны при различном количестве учитываемых ПГ. Результаты математического моделирования сравниваются с данными, полученными экспериментальным путем.
Результаты расчетов, иллюстрирующие зависимости угла падения (-1)m, соответствующего преобразованию с максимальной эффективностью энергии падающей однородной плоской Н-поляризованной волны в энергию (-1)-й поверхностной гармоники и постоянной вытекания (-1) для соответствующей гармоники от количества учитываемых гармоник, приведены в табл. 2.2. В качестве материала ПДВ выбран полистирол ( r=2.56, tg э < 0.001) толщиной t=6 мм; период d каждой из трех исследуемых гребенок выбран равным 24 мм; ширина пазов ДР W=8 мм (W < min/2). Параметры структуры выбраны таким образом, чтобы частота брэгговского резонанса второго порядка лежала в исследуемом диапазоне частот. Методика определения постоянной вытекания
(-1) приведена в главе 3.

Таблица 2.2 Зависимости дисперсионных характеристик от числа учтенных ПГ
|
|
|
Эксперимент |
Абсолют. |
|
|
|
|
||
Кол-во гармоник |
Угол |
Постоян. |
альные |
отклонение |
|
|
|
|
||
(-1)m, |
вытека- |
значения |
расчета от |
|
|
|
|
|||
|
|
|
|
|
||||||
|
град. |
ния, |
величин |
эксперимента |
Примечание |
|
||||
|
|
(-1), 1/м |
(-1)m, |
(-1), |
(-1)m, |
(-1), |
|
|
|
|
|
|
|
град |
1/м |
град |
1/м |
|
|
|
|
|
|
|
R=5 мм; f=9,8 ГГц; h1=4 мм |
|
|
|
|
|||
|
|
|
5.60 |
5.50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
4.44 |
6.88 |
|
|
1.16 |
-1.33 |
|
|
|
|
11 |
4.60 |
6.43 |
|
|
1.00 |
-0.93 |
Сходимость |
|
||
13 |
4.65 |
6.43 |
|
|
0.95 |
-0.93 |
вычислений |
при |
||
15 |
4.80 |
5.91 |
|
|
0.80 |
-0.41 |
определении |
|
||
17 |
4.90 |
5.91 |
|
|
0.70 |
-0.41 |
величин |
|
(-1)m и |
(-1) |
19 |
4.90 |
5.91 |
|
|
0.70 |
-0.41 |
близка |
|
|
к |
21 |
4.90 |
5.53 |
|
|
0.70 |
-0.03 |
экспоненциальной |
|||
23 |
5.00 |
5.53 |
|
|
0.60 |
-0.03 |
|
|
|
|
25 |
4.90 |
5.53 |
|
|
0.70 |
-0.03 |
|
|
|
|
|
|
|
R=7 мм; f=12 ГГц; h1=9.2 мм |
|
|
|
|
|||
|
|
|
-5.40 |
0.40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
-5.63 |
0.78 |
|
|
0.23 |
-0.38 |
|
|
|
|
7 |
-5.28 |
0.38 |
|
|
-0.12 |
0.02 |
При |
|
малых |
|
9 |
-5.28 |
0.36 |
|
|
-0.12 |
0.04 |
значениях |
|
|
|
11 |
-5.28 |
0.36 |
|
|
-0.12 |
0.04 |
постоянной |
|
||
13 |
-5.26 |
0.34 |
|
|
-0.14 |
0.06 |
вытекания |
ошибка |
||
15 |
-5.26 |
0.34 |
|
|
-0.14 |
0.06 |
ее |
определения |
||
17 |
-5.26 |
0.34 |
|
|
-0.14 |
0.06 |
наиболее велика |
|
||
19 |
-5.26 |
0.34 |
|
|
-0.14 |
0.06 |
|
|
|
|
|
|
|
R=15 мм; f=10 ГГц ; h1=6.6 мм |
|
|
|
|
|||
|
|
|
10.50 |
1.63 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5 |
9.36 |
2.02 |
|
|
1.14 |
-0.39 |
Для |
обеспечения |
||
7 |
9.46 |
1.80 |
|
|
1.04 |
-0.17 |
одинаковой |
|
||
9 |
9.44 |
1.80 |
|
|
1.06 |
-0.17 |
относительной |
|
||
11 |
9.42 |
1.76 |
|
|
1.08 |
-0.13 |
ошибки определения |
|||
13 |
9.42 |
1.73 |
|
|
1.08 |
-0.10 |
величин |
(-1)m и |
(-1) |
|
15 |
9.42 |
1.76 |
|
|
1.08 |
-0.13 |
требуется |
учитывать |
||
17 |
9.42 |
1.76 |
|
|
1.08 |
-0.13 |
разное |
количество |
||
19 |
9.42 |
1.76 |
|
|
1.08 |
-0.13 |
ПГ |
|
|
|

Результаты, приведенные в табл. 2.2, подтверждают тот факт, что использование метода редуцирования в задачах дифракции на координатных структурах приводит к покоординатной сходимости комплексных амплитуд пространственных гармоник Флоке. Для обеспечения точности, необходимой для инженерных расчетов, в различных случаях для анализируемой структуры следует учитывать от 9 до 25 гармоник, причем в областях частот, близких к глубинным резонансам канавок ДР и брэгговскому резонансу второго порядка необходимое количество гармоник увеличивается. Учет потерь в диэлектрике приводит к изменению исследуемых параметров на 1-3 %.
Оценка границ области применимости приведенной математической модели дифракции плоской однородной Н-поляризованной волны на двумернопериодичной металлической гребенке, накрытой слоем диэлектрика, и выяснение основных физических закономерностей, обусловленных двойной периодичностью исследуемой структуры, влияющих на ее дисперсионные характеристики, а также выработка рекомендаций по ее алгоритмизации требует выяснения зависимости величины поправки h от геометрических параметров электродинамической системы «двумерно-периодичная идеально проводящая гребенка + диэлектрический волновод». Важность знания поведения данных зависимостей обусловлена тем, что величина поправки h определяет отличия дисперсионных свойств двумерно-периодичной и одномерно-периодичной гребенок с диэлектрическим слоем.
Ниже для наглядности результаты компьютерного моделирования вышеуказанных зависимостей приведены для абсолютных значений частоты падающей плоской однородной Н-поляризованной волны и параметров двумерно-периодичной металлодиэлектрической структуры.
Зависимость поправки h, учитывающей проникновение падающих на структуру волн в запредельные пазы ДР, от величины прицельного расстояния R1 приведена на рис. 2.24 для следующих параметров структуры: r=2.56,
W=8 мм, t=6 мм, h1=30 мм, (-1)m=00. Кривая 1 соответствует частоте падающей волны f=9.4 ГГц ( 0=3.2 см), а зависимость 2 - частоте f=12 ГГц ( 0=2.5 см).
Видно, что зависимости являются периодическими, причем периоды равны половине длины волны в свободном пространстве для соответствующего значения частоты. Через интервалы изменения прицельного расстояния R1, равные четверти длины волны в свободном пространстве, происходит смена минимальных и максимальных значений поправки, используемой для построения эквивалентной одномерно-периодичной структуры, вызванная тем, что при вариации прицельного расстояния периодически изменяется реактивное сопротивление поверхностной волны в планарном диэлектрическом волноводе, вносимое в пазы ДР (воздушный зазор трансформирует это сопротивление). Вариация толщины зазора на четверть длины волны инвертирует величину вносимого сопротивления и влияет на его характер, а
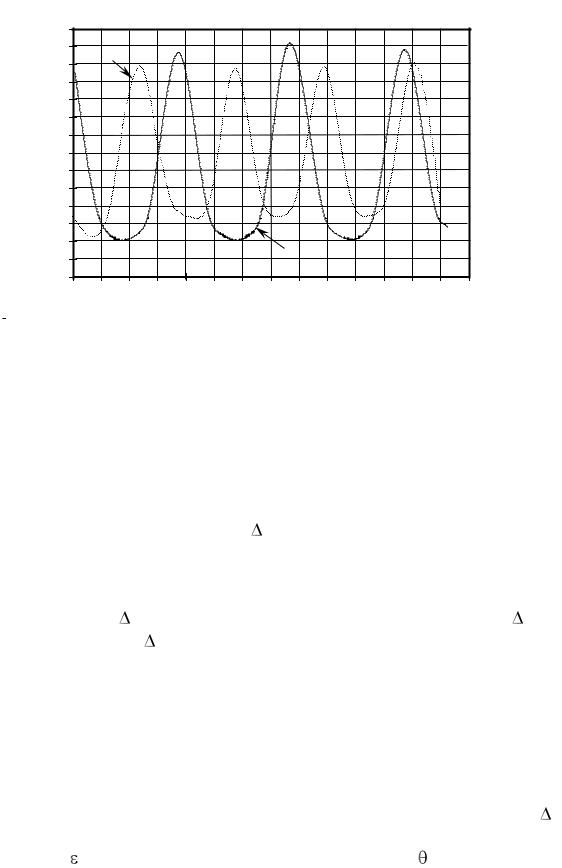
изменение на половину длины волны оставляет вносимое сопротивление |
|||||||||||||||
прежним. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 .4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 .4 h, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 .3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мм |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 .2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 .1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 .9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v yi |
0 .8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 .7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 .6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 .5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 .4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 .3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 .2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 .1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
4 |
8 |
1 2 |
1 6 |
2 0 |
2 4 |
2 8 |
3 2 |
3 6 |
4 0 |
4 4 |
4 8 |
5 2 |
5 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1,мм |
|
0 |
|
|
|
|
|
|
xi X |
|
|
|
|
|
|
5 6 |
Рис. 2.24. Зависимости поправок h от величины прицельного расстояния |
|||||||||||||||
Из рис. 2.24 следует, что свойства одномерно- и двумерно-периодичных структур могут незначительно отличаться (на участках с минимальной величиной поправки) и иметь значительную разницу при других величинах прицельного расстояния, соответствующих большим значениям поправки. Отсюда вытекает важный практический вывод: существуют такие диапазоны изменения прицельного расстояния, в пределах которых для анализа свойств двумерно-периодичной структуры можно воспользоваться математической моделью, описывающей свойства одномерно-периодичной структуры (так как соответствующая величина поправки h пренебрежимо мала).
Для оптимизации времени компьютерного моделирования и точности получаемых результатов при автоматизированном проектировании дифракционных плоских антенн СВЧ диапазона волн целесообразно оценивать величину поправки h. В случае небольших значений поправки h (ниже пороговой величины hпор, определяемой заданным верхним пределом допустимого уровня погрешности определения антенных характеристик моделируемой структуры) имеет смысл использовать математическую модель для одномерно-периодичной структуры с теми же геометрическими размерами и электрическими параметрами материалов, что и у двумерно-периодичной. Использование избирательного к входным данным подхода к математическому моделированию позволяет в подобных случаях почти вдвое сократить затраты необходимого для моделирования машинного времени.
Кривые, демонстрирующие зависимости величины поправки h от ширины пазов ДР, показаны на рис. 2.25. Параметры структуры выбраны следующими: r=2.56, d=24 мм, h1=4 мм, f=9.4 ГГц, (-1)m=00. Приводятся зависимости для нескольких значений прицельного расстояния: R=7 мм, 10 мм, 13 мм, 15 мм. При любом прицельном расстоянии сужение пазов ДР ведет к

снижению поправки h, так как при уменьшении ширины пазов ДР в |
|||||||||||||
запредельные области структуры просачивается меньшая доля энергии, что |
|||||||||||||
ослабляет различия в свойствах одномерно- и двумерно-периодичных структур. |
|||||||||||||
Поэтому при проектировании ПДА следует иметь в виду, что в случае |
|||||||||||||
достаточно узких канавок ДР (W |
0/6) для расчетов можно воспользоваться |
||||||||||||
одномерно-периодичной моделью. |
|
|
|
|
|
|
|
|
|||||
|
h, |
|
|
|
|
|
|
|
|
|
|
|
|
1 .7 |
1 |
.7 |
|
|
|
|
|
|
|
|
|
|
|
мм |
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
.6 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
.5 |
|
|
|
|
|
|
R1=15 мм |
|
|
|
|
|
1 |
.4 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
.3 |
|
|
|
|
|
|
|
|
|
|
|
v yi |
1 |
.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y( x ) |
1 |
.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v y1 i |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 1( x ) |
0 .9 |
|
|
|
|
|
|
|
|
|
|
|
|
v y2 i |
0 .8 |
|
|
|
|
|
|
|
13 мм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 2( x ) |
0 .7 |
|
|
|
|
|
|
|
|
|
|
|
|
v y3 i |
0 |
.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y 3( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
.5 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
.4 |
|
|
|
|
|
|
|
10 мм |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
.3 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
.2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
.1 |
|
|
|
|
|
|
|
|
|
7 мм |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
|
5 |
6 |
7 |
8 |
9 |
1 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
W,мм |
|
|
0 |
|
|
|
|
x |
|
X |
|
|
|
1 0 |
Рис. 2.25. Зависимости поправки |
|
i h от ширины пазов решетки W |
|||||||||||
Как влияет на поправку h глубина пазов ДР, иллюстрируется рис. 2.26.
Графики |
построены для следующих входных данных: r=2.56, |
d=24 мм, |
|
W=8 мм, |
t=6 |
мм, f=9.4 ГГц, (-1)m=0 . Моделирование проведено для тех же |
|
значений прицельного расстояния, что и для рис. 2.25. |
|
||
Обращает на себя внимание тот факт, что каждая из кривых может быть |
|||
разделена |
(вертикальной пунктирной прямой) на два участка: 1 |
«область |
|
нарастания» |
при малых значениях глубины пазов ДР h1 величина поправки h |
||
быстро и монотонно растет с увеличением h1 (интервал h1 от 0 до 6 мм) и 2 – «область насыщения», где увеличение глубины пазов ДР (интервал h1 > 6 мм) не приводит к заметным изменениям величины поправки.
В большей части области 1 величина поправки пропорциональна глубине пазов ДР: при дифракции Е-поляризованной волны на гребенке с мелкими пазами эквивалентная отражающая плоскость (рис. 2.17) может быть смещена от вершин ребер решетки на расстояние X0, равное или превышающее
