3364

периодическое условие – равенство нормальных компонент ускорения и давлений на выбранных границах.

Если в качестве среды в модели выступает ламинарная жидкость, то для её описания используется система уравнений Навье-Стокса:

тему уравнений, необходимы материальные соотношения. Так, например, для ньютоновских жидкостей в качестве такого соотношения выступает выражение для тензора вязких напряжений:

где динамическая вязкость (Па с) зависит от термодинамического состояния жидкости и не зависит от скорости.

Для ламинарной жидкости существует две модели – сжимаемая (плотность меняется во времени) и несжимаемая ( = const). В случае сжимаемой жидкости уравнение примет вид:

Вслучае несжимаемой жидкости:

∙ = 0,

+ ( ∙ ) = ∙ − + ( +( ) ) + .

Ниже представлены основные граничные условия, предназначенные для задач гидродинамики в базовом модуле:

172

сжимаемой жидкости последний член в скобках отсутствует), где – напряжение на границе, т.е. сила, действующая на еди-

= – задание поля скорости на границе;

= – задание значения давления на границе;

периодическое условие – равенство давлений и скоростей на выбранных границах.

Для моделей, включающих в себя расчёт деформаций тела, в базовом модуле COMSOL Multiphysics имеются дифференциальные уравнения, реализующие модель линейноупругого материала. Переменной в этих уравнениях служит вектор смещения , компонентами которого являются деформации тела в направлениях, параллельных координатным осям. Размерность вектора равна размерности геометрии. Само уравнение имеет вид:

3D-геометриях и Н/м2 в 2D-геометриях), а тензор напряжений второго ранга выражается по закону Гука-Дюамеля:

=+ :( − ),

или в коэффициентной форме

173

и – начальные напряжения и деформации соответственно. Если требуется решить задачу на собственные значения или собственные частоты, то дифференциальное уравнение

(П1.7) примет вид:

где – собственная частота, связанная с соответствующим собственным значением через мнимую единицу: = − .

В этом случае возможно ввести демпфирование путём модификации соотношения для тензора напряжений:

ряется в Н/м);

∙ = 0, т.е. равенство нулю нормальной компоненты вектора смещений на границе;

периодическое условие – равенство компонент вектора смещения на выбранных границах.

174

ПРИЛОЖЕНИЕ 2 Описание процедуры численного решения краевой задачи

для скалярного и векторного уравнений Лапласа с помощью Comsol Multiphysics

Пусть имеется сверхпроводящее тело (или совокупность тел), которое помещено во внешнее однородное магнитное поле. Тело находится в мейсснеровском состоянии, т.е. магнитное поле полностью выталкивается из толщи сверхпроводника, проникая лишь на малую глубину, которой можно пренебречь по сравнению с характерными размерами тела. Требуется найти распределение магнитного поля вокруг сверхпроводящего тела. Эта задача решается при помощи введения магнитного потенциала – скалярного потенциала для случая, когда сверхпроводящее тело представляет собой односвязную область (шар, эллипсоид, цилиндр и т.д. или в случае совокупности сверхпроводящих тел все тела представляют собой односвязную область) или векторного потенциала , если сверхпроводящее тело – многосвязная область (например, тор или совокупность многосвязных и односвязных тел). Вектор напряжённости магнитного поля и вектор магнитной индукции выражаются через скалярный и векторный магнитный потенциал соответственно следующим образом:

=− ,

=× .

Магнитный потенциал во внешней по отношению к сверхпроводящему телу области описывается следующими уравнениями:

175

ласть. Если эта среда однородная, т.е. = const, то данные уравнения сводятся к уравнениям Лапласа – скалярному и векторному соответственно:

∆= 0,

∆= .

Внутри сверхпроводящего тела, как уже было сказано, поле отсутствует, т.е. магнитный потенциал в этой области равен нулю. Таким образом, область, занятая сверхпроводящим телом, может быть исключена из геометрии при решении задачи. На границе сверхпроводящего тела задаётся условие непроникновения поля в тело. Для задачи в постановке скалярного потенциала оно имеет вид:

∙= 0,

адля задачи в постановке векторного потенциала –

×= .

На границе внешней по отношению к сверхпроводящим телам области задаётся значение вектора магнитной индукции или вектора напряжённости внешнего магнитного поля:

,

нитной индукции и вектор напряжённости внешнего магнитного поля соответственно.

В случае, когда рассматривается совокупность сверхпроводящих тел, предметом исследований также является сила магнитного взаимодействия между телами, а также изучение возможности устойчивого подвеса одного из тел в неоднородном магнитном поле, образующимся вблизи других сверхпроводящих тел.

176

Пример 1. Найти распределение магнитного поля в окрестности сверхпроводящего шара в мейсснеровском состоянии, помещённого во внешнее однородное магнитное поле с индукцией 0.05 Тл.

Порядок выполнения работы:

1)Запустить COMSOL Multiphysics 4.2.

2)В окне мастера построения модели (Model Wizard) в разделе выбора размерности геометрии (Select Space Dimension) выбрать 3D; нажать «Далее» (Next).

3)В разделе выбора физического интерфейса в модуле

AC/DC выбрать интерфейс Magnetic Fields, No Currents, щёлк-

нуть по нему 2 раза, нажать «Далее».

4)В разделе выбора типа задачи (Select Study Type) выбрать стационарный тип задачи (Stationary); нажать Finish. После этого откроется рабочее пространство COMSOL Multiphysics, которое состоит из дерева модели, окна настроек и графического окна.

5)Задаётся геометрия модели. В дереве модели за это от-

вечает узел Geometry1 (Model 1 > Geometry 1). В контекстном меню этого узла, которое вызывается путём нажатия правой кнопкой мыши, выбрать сферу (Sphere). В окне настроек в разделе «Радиус и форма» (Radius and Shape) в поле «Радиус» (Radius) ввести 0.1. Вверху окна настроек нажать кнопку «Построить выбранный объект» (Build Selected). Таким образом, будет построен шар радиусом 10 сантиметров с центром в начале координат, который представляет собой сверхпроводящее тело. Повторить ту же процедуру, только в поле «Радиус» ввести 1, т.е. построить концентрический с первым шар радиусом 1 метр, который представляет собой внешнюю по отношению

ксверхпроводящему шару область.

6)Поскольку внутри шара в мейсснеровском состоянии поле отсутствует, область, представляющую собой сверхпроводящий шар, можно исключить из геометрии. Для этого необходимо в контекстном меню узла Geometry выбрать (Boolean Operations > Difference). В окне Difference в поле Objects to add

177

добавить внешнюю область, предварительно нажав справа от поля кнопку Activate selection. Область добавляется путём выделения этой области левой кнопкой мыши в графическом окне (после этого она подсвечивается красным) и нажатия на неё правой кнопкой мыши (после этого она подсвечивается синим цветом). Аналогичным образом в поле Objects to substract добавляется внутренняя область. Для того, чтобы её выделить, для удобства можно воспользоваться опциями установления прозрачности (Transparency) или отображения только каркаса поверхностей, составляющих геометрию (Wireframe Rendering). Эти опции можно активировать, нажав на иконки с изображением прозрачного куба или каркаса куба в верхней части графического окна. После нажатия кнопки Build Selected область, занятая сверхпроводящим шаром, будет вырезана из геометрии.

7) Задать уравнение, описывающее распределение магнитного поля в области. Это осуществляется путём выбора в узле Magnetic Fields, No Currents узла Magnetic Flux Conservation 1. Для корректного задания уравнения в окне настроек в разделе Magnetic Fields в поле надо поменять From Material

на User Defined, так, что относительная магнитная проницаемость в области будет равна 1.

8)Задать условие равенства индукции магнитного поля

0.05Тл на внешней границе внешней области. Для этого в контекстном меню узла Magnetic Fields, No Currents необхо-

димо выбрать команду Magnetic Flux Density (Вектор магнитной индукции). Сначала добавляются границы, на которых это условие задаётся. Это осуществляется путём выделения соответствующих границ и нажатия на них правой кнопкой мыши. После этого в окне настроек в разделе «Выбор границ» (Boundary Selection) должны появиться границы с номерами 1, 2, 3, 4, 9, 10, 13, 16. В разделе Magnetic Flux Density в поле Type на-

На оставшихся границах остаётся граничное условие по умолчанию – магнитная изоляция.

178

10)Разбиение расчётной области на конечные элементы осуществляется в узле Mesh 1. В окне настроек в разделе «Настройки сетки» (Mesh Settings) в поле «Размер элементов»

(Element size) выбрать Extremely Fine. Нажать кнопку Build All

вверхней части окна настроек.

11)Расчёт задачи запускается при выполнении команды «Рассчитать» (Compute) в контекстном меню узла Study 1.

12)Вывести модуль вектора магнитной индукции вдоль вертикальной оси и в горизонтальной плоскости (например, вдоль оси Oy).

Рис. П2.1. Задание вектора магнитной индукции на границе внешней области

В контекстном меню узла «Множества данных» (Data Sets), который находится в узле Results выбрать Cut Line 3D. В окне настроек в разделе Line Data в поле «Точка 1» (Point 1) ввести числа (0, -1, 0), а в поле Point 2 – (0, 1, 0). Повторить эту операцию и для новой линии задать координаты точек (0, 0, -1) и (0, 0, 1). Таким образом, получится прямая, вдоль которой нужно будет вывести модуль вектора магнитной индукции.

13)Выбрать в контекстном меню узла Results опцию «1D

–графики» (1D Plot Group) и в контекстном меню появившего-

179

ся узла 1D Plot Group 2 выбрать опцию «График» (Line Graph).

В окне настроек появившегося узла Line Graph 1 в разделе «Данные» (Data) в поле «Множество данных» (Data set) выбрать Cut Line 3D 1. В разделе «Данные по оси y» (y-axis Data) нажать на иконку с двумя стрелками (Replace Expression) и из всплы-

вающего меню выбрать Magnetic Fields, No currents > Magnetic flux density, norm (mfnc.normB). Таким образом, по оси y на графике будут откладываться значения модуля вектора магнитной индукции. В разделе x-axis Data в поле Parameter заменить

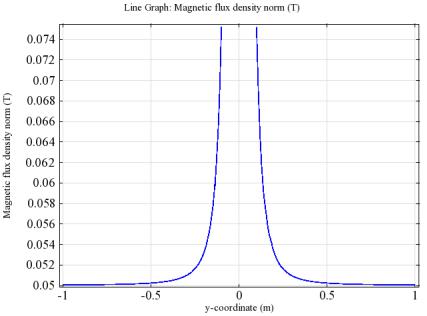
Arc Length на Expression и в поле Expression набрать y. Таким образом, данный график будет иллюстрировать распределение модуля вектора магнитной индукции вдоль оси y глобальной системы координат. Нажать кнопку «Нарисовать» (Plot) в верхней части окна настроек (рис. П2.2).

Рис. П2.2. Распределение модуля вектора магнитной индукции вдоль оси y

180