3237

А.П. Бырдин Н.В. Заварзин А.А. Сидоренко Л.П. Цуканова

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

Учебное пособие

Воронеж 2012

0

УДК 517.2

Вычислительная математика: учеб. пособие / А.П. Бырдин, Н.В. Заварзин, А.А. Сидоренко, Л.П. Цуканова. Воронеж: ФГБОУВПО “Воронежский государственный технический университет”, 2012. 176 с.

В учебном пособии излагаются элементы вычислительной математики применительно к задачам робототехники.

профессионального образования по направлению подготовки бакалавров 221010 «Промышленная и специальная робототехника», профиль «Мехатроника и робототехника», дисциплине ”Математика”.

Предназначено для студентов очной формы обучения. Учебное пособие подготовлено в электронном виде в

текстовом редакторе Word 2003 и содержится в файле ВычМат-Робототехника.doc.

Табл. 24. Ил. 20. Библиогр.: 10 назв.

Научный редактор д-р физ.-мат. наук, проф. В.Д. Репников

Рецензенты: кафедра математического моделирования Воронежского государственного университета (зав. кафедрой д-р физ.-мат. наук, проф. В.А. Костин); канд. техн. наук, доц. А.В. Паринов

Бырдин А.П., Заварзин Н.В., Сидоренко А.А., Цуканова Л.П., 2012

Оформление. ФГБОУВПО “Воронежский государственный технический университет”, 2012

2

1. ДЕЙСТВИЯ НАД ПРИБЛИЖЕННЫМИ ЧИСЛАМИ

1.1. Основные источники погрешностей

Решение многих прикладных задач связано с применением численных методов. Поэтому получить точное решение таких задач практически невозможно. Полученные

несколько групп.

1.Погрешности, связанные с самой постановкой математической задачи (погрешность задачи). В частности, неточно заданы исходные данные.

2.Применяемые для решения задач методы, в большинстве случаев, являются приближенными. Используемые в математических формулах числовые параметры могут быть определены лишь приближенно. Таковы, например, многие физические константы.

3.Погрешности, связанные с действиями над приближенными числами (погрешности действий). Так при вводе исходных данных, при выполнении арифметических действий, при получении результатов производится округление этих чисел.

числа a понимается разность между соответствующим точным числом A и данным приближенным, т.е.

4

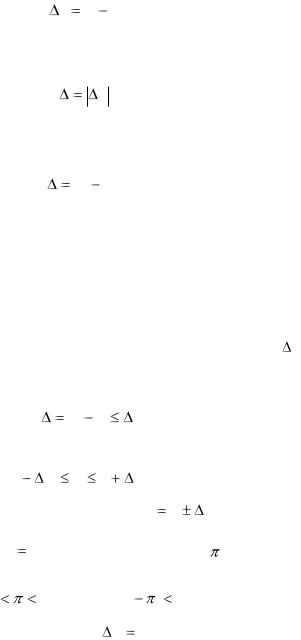
a A a .

Во многих случаях знак ошибки неизвестен. Тогда целесообразно пользоваться абсолютной погрешностью приближенного числа

a .

Абсолютной погрешностью приближенного числа называется абсолютная величина разности между истинным и приближенным значениями

практически не может использоваться.

В этом случае полезно вместо неизвестной теоретической абсолютной погрешности ввести ее оценку сверху, так называемую предельную абсолютную погрешность.

Если учесть, что

5

Для приближенного числа, полученного в результате округления, абсолютная погрешность принимается равной половине единицы последнего разряда числа. Например,

a0.0005.

Примеры оценки абсолютной погрешности при

некоторых значениях приближенной величины a (таблица 1):

Абсолютная погрешность (или предельная абсолютная погрешность) не достаточна для характеристики точности измерения или вычисления. Так, например, если при измерении длин двух стержней получены результаты l1

и l2 5.3см 0.1см , то, несмотря на совпадение предельных

абсолютных погрешностей, качество первого измерения выше, чем второго. Для точности данных измерений существенна абсолютная погрешность, приходящаяся на единицу длины, которая носит название относительной погрешности.

Относительной погрешностью приближенного числа а называется отношение абсолютной погрешности к модулю точного числа

Так же как и для абсолютной погрешности, введем понятие предельной относительной погрешности.

6

В приближенных вычислениях нужно учитывать следующие правила действия с приближенными числами.

1.Предельная абсолютная погрешность суммы

суммы не превышает наибольшей из относительных погрешностей слагаемых

7

погрешности чисел a1 и a2 .

4.Предельная абсолютная погрешность произведения

двух сомножителей a a1 a2 вычисляется по формуле

а предельная относительная погрешность произведения равна сумме предельных относительных погрешностей

8

6. При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:

Пример. Найти относительную погрешность функции:

a2 = 18 = 4.2426... . Затем вычисляем предельные абсолютные

9