3237

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

k4 h f x h, y k3

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

3.63 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 1815 16 17 18 > Следующая >>>

точность только для уравнений с достаточно гладкой правой частью.

Пример. Используя метод Эйлера, найти значения функции y , определяемой дифференциальным уравнением

при начальном

условии

y(0)

шаг

h 0.1 .

Ограничиться отысканием первых четырех значений

y .

Решение.

Находим

последовательные

значения

аргумента:

0 ,

0.1, x2

0.2 , x3

0.3 .

Вычислим

соответствующие значения искомой функции:

h f (x0 , y0 )

0.1 (1

(1 0)

1.1;

f (x1, y1)

1.1

0.1 (1.1

0.1) (1.1

0.1)

1.183;

f (x2 , y2 )

1.183

0.1 (1.183

0.2) (1.183

0.2)

1.254;

h f (x3 , y3 )

1.254

0.1 (1.254

0.3) (1.254 0.3)

1.315 .

Таким образом, получаем таблицу 22:

Таблица 22

0.1

0.2

0.3

1.1

1.18

1.31

7.4. Исправленный метод Эйлера

Пусть

найдено

приближенное

значение

y(xi )

решения

задачи

(7.1)

(7.2)

требуется

вычислить

y(xi

1) , где xi

h . Запишем разложение решения

по формуле Тейлора,

принимая за базовую точку

(т.е. по

степеням

xi )

положим в этом разложении x

xi 1 .

Имеем

140

y(xi 1) y(xi ) hy (xi )	h2	y (xi ) ...	1	hn y (n) (xi ) O(hn 1).
	2		n!

Если ограничиваться двумя слагаемыми в правой части этого разложения, то получим обычный метод Эйлера (7.7). Будем учитывать третье слагаемое. Тогда при n 2 следует равенство

			h2
y(xi 1 )	y(xi ) hy (xi )			y (xi ) O(h3 ).	(7.10)
y(xi 1 )	y(xi ) hy (xi )	2		y (xi ) O(h3 ).	(7.10)
		2
Значение	первой производной в точке xi , в силу (7.1),
приближенно	известно	y (xi ) f (xi , y(xi ))			f (xi , yi ) .

Дифференцируя (7.1), по формуле полной производной получим

y(x) f x (x, y) f y (x, y) y

находим приближенное значение второй производной

y(xi ) 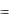f x (xi , y(xi )) f y (xi , y(xi )) f (xi , y(xi )) f x (xi , yi ) f y (xi , yi ) f (xi , yi ).

Подставляя приближенные выражения

y(xi ) ,

y (xi ) и

y (xi )

в равенство (7.10), получаем следующую формулу для

вычисления yi

y(xi

при i

0,1,..., n :

h f (x , y

)

(x , y

)

(x , y

)

f (x , y

) .(7.11)

i 1

i i

Определяемый ее метод называется исправленным

методом Эйлера.

Так

как

при i

0 формула (7.10)

точна, а

y(x0 ) ,

согласно начальному условию (7.2), то на первом шаге вычислений по формуле (7.11) будет совершаться ошибка, связанная только с усечением ряда Тейлора. Следовательно, шаговая погрешность метода (7.11) составляет величину

141

O(h3 ) , а это означает, что исправленный метод Эйлера относится к методам второго порядка.

7.5. Методы Рунге-Кутта

Эти методы позволяют строить схемы различного порядка точности. Методы Рунге-Кутта очень удобны как для расчетов на ЭВМ, так и для “ручных” расчетов. Сейчас они являются наиболее употребительными в практических вычислениях. В их основе лежит модификация метода Эйлера.

Рассмотрим сначала один из возможных способов

уточнения метода Эйлера. Пусть на

шаге

(при

xk )

получено значение

yk .

Найдем следующее значение

1 по

методу

Эйлера.

Для этого вычислим

f (xk , yk )

и проведем

отрезок

M k M k

1 :

yk 1

hf (xk , yk ) .

Обозначим

f (xk , yk ) ;

tg 1

m1 . В середине наклон интегральной

кривой:

N k (xk

; yk

m1h

tg 2 ,

f (xk

, yk

m1h

) . (7.12)

По этому наклону определяем приращение функции на

целом шаге

yk 1

m2 h;

f (xk , yk );

f (xk

, yk

m1h

) .

Геометрически это значит, что с угловым коэффициентом

tg 2

проводим отрезок

M k M k

1 .

Этим производится

пересчет (уточнение) углового коэффициента звеньев ломаной, аппроксимирующей интегральную кривую. Данный алгоритм (7.12) учитывает поворот касательной к интегральной кривой на отрезке xk , xk 1 .

Доказывается, что если f (x, y) непрерывна и ограничена вместе со своими производными второго порядка, то формула

142

(7.12) имеет второй порядок точности, т.е. суммарная погрешность на отрезке a, bимеет порядок малости h2 .

Формула (7.12) называется двучленной формулой РунгеКутта. Она имеет неплохую точность и нередко используется в численных расчетах. Двучленных схем метода Рунге-Кутта существует бесконечно много.

Метод Рунге-Кутта допускает построение схем различного порядка точности. Например, метод Эйлера можно

рассматривать как схему Рунге-Кутта	первого порядка
точности. Наиболее употребительны	схемы четвертого

порядка точности, образующие семейство четырехчленных схем. Их также бесконечно много. Приведем без доказательства ту из них, которая записана в большинстве стандартных программ для ПЭВМ:

f (k

n 1

f (x

, y

), k

f (x

, y

k ),

n 2 1

(7.13)

f (xn

, yn

2 ),

f (xn

h, yn

hk3 ).

Погрешность этого метода на полном отрезке составляет h4 , т.е. R ~ h 4 .

Замечание 1. Метод Рунге-Кутта (7.13) имеет высокую точность только для достаточно гладких функций f (x, y) .

Действительно, оценка погрешности предполагает, что правая часть уравнения имеет непрерывные производные до четвертого порядка включительно (следует из формулы Тейлора).

Замечание 2. Все схемы Рунге-Кутта допускают расчет с переменным шагом.

143

Замечание 3.

Для оценки погрешности вычислений и для

контроля

за

выбором величины шага обычно применяют

двойной пересчет.

Пусть m -четное и yh (xm ),

y2h (xm ) -

значения

приближенных

решений,

вычисленных

соответственно

шагами

и 2h .

Как и

для

формулы

Симпсона можно доказать, что

y(xm )

yh (xm )

y2h (xm )

(7.14)

где y(xm ) - точное решение в точке xm .

Отсюда вытекает следующий алгоритм регулирования шага: если правая часть (7.14) не превосходит заданной погрешности, то шаг выбран правильно. Если при этом правая часть в (7.14) существенно меньше заданной погрешности, то шаг можно удвоить. Если же правая часть в (7.14) больше заданной погрешности, то шаг следует уменьшить вдвое.

Недостатком метода Рунге-Кутта четвертого порядка (7.13) является необходимость на каждом шаге вычислять

четыре раза значения							f (x, y) , что вызывает неудобства при
сложном виде этой функции.
Пример.				Методом						Рунге			– Кутта проинтегрировать
уравнение		x 2 y		xy		1		при			начальном					условии y(1)					0 в
промежутке 1;2 ; шаг h									0.2		. [точное решение						y		x 2	1	].
промежутке 1;2 ; шаг h									0.2		. [точное решение						y		2x		].
																			2x
Решение. Здесь						f (x, y)						y	1	.
Решение. Здесь						f (x, y)								.
												x	x2
Найдем числа:
k1	h	f (x, y)				0.2			0		1		0.2;

									1		12
									1		12
k2	h	f	x		h	, y		k1			0.2			0.1	1		0.18;

					2			2						1.1	1.12
					2			2						1.1	1.12
k3	h	f	x		h	, y		k	2		0.2			0.09	1			0.18;

					2			2						1.1	1.12
					2			2						1.1	1.12

144

Следовательно,

y		1	(k		2k		2k		k		)	0.18 ,
	0					2		3		4
		6		1

т.е.		y1			y0		y0		0	0.18		0.18 .

Аналогичным образом находим
k1	h		f (x, y)						0.2			0.18						1			0.17;

													1.2			1.22
													1.2			1.22
k2	h		f	x			h		, y		k1			0.2					0.26			1
k2	h		f	x			2		, y	2				0.2				1.3			1.32
							2			2								1.3			1.32
k3	h	f		x		h		, y		k2			0.2					0.25			1
k3	h	f		x	2			, y		2			0.2					1.3		1.32
					2					2								1.3		1.32
k4	h		f	x		h, y				k3			0.2					0.33			1

																		1.4			1.42
																		1.4			1.42
Следовательно,
y		1	(k			2k				2k			k		)			0.15 ,
y			(k			2k			2	2k		3	k	4	)			0.15 ,
1		6		1					2			3		4
		6
т.е. y2	y1				y1				0.18				0.15				0.33 и т.д.

0.15;

0.14.

Метод Рунге-Кутта легко переносится на нормальные системы дифференциальных уравнений. Как для метода Эйлера, запишем задачу Коши для нее в векторной форме

		Y (x)	F (x,Y )
		Y (x0 )	Y0 ,
где	Y (x)	y1 (x); y2 (x);...; yn (x) ,		Y0	y10 , y20 ,..., yn0 ,
F	f1, f2 ,...,	fn .
	Для получения расчетных формул метода Рунге-Кутта
достаточно в формулах (7.13) заменить				y,	f (x, y), y0 , ki на

145

Y ,F (x,Y ),Ki , ( i 1,2,3,4 ) т.е. внести соответствующие

массивы переменных.

Рассмотренные методы Эйлера и Рунге-Кутта являются одношаговыми методами, поскольку для вычисления yn 1 используется лишь значение решения в предыдущей точке, а именно yn . Это позволяет начать расчет при n 0 по известным начальным значениям.

Задачи для самостоятельного решения

1.Методом Эйлера найти три значения функции y ,

определяемой

уравнением

y 2 ,

при начальном

условии y(0)

полагая

0.1 .

Методом Эйлера

найти четыре значения функции y ,

определяемой уравнением y

x 2

y3 , при начальном условии

y(0)

полагая

0.1 .

3. Методом Эйлера найти численное решение уравнения

y)(1

xy)

на отрезке

0;1

при начальном

условии

2 y

y(0)

с шагом

0.2 .

Методом Рунге – Кутта проинтегрировать уравнение

4 y

y 2

4x2 , y(0)

1 в промежутке

0;1

с шагом

0.1 .

Вычисления вести с тремя верными знаками.

Методом Рунге – Кутта проинтегрировать уравнение

0.5y ,

y(0)

1 в промежутке

0;1

с шагом

0.1 .

Вычисления вести с тремя верными знаками.

146

8. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

			8.1.	Постановка задачи
Рассмотрим			двухточечные			краевые		задачи			для
обыкновенных		дифференциальных				уравнений				второго
порядка. Общий вид таких задач
		F(x, y, y , y ) 0 ,			x	[a,b] ,					(8.1)
	1( y(a), y (a)) 0 ,				2 ( y(b), y (b)) 0 ,
где F, 1,	2	- заданные функции				определенной			гладкости.
Наиболее употребительны и лучше всего изучены									линейные
краевые задачи, т.е. задачи вида (8.1), в которых								F,		1 и	2
линейные функции.
Пусть	требуется			найти	решение		этого		уравнения
y y(x) ,	для которого искомая функция						y	y(x)		и	ее
производная y (x)			на концах отрезка a, b удовлетворяет двум

независимым	между собой краевым условиям,					в общем случае
нелинейным
	W1 y(a), y (a);y(b), y (b)				0	(8.2)
	W2 y(a), y (a);y(b), y (b)				0.

Такого типа задачи часто встречаются в приложениях -
теории колебаний,		динамике твердого тела и т.п.
Рассмотрим некоторые примеры постановки задач.
Пример. Простейшая двухточечная краевая задача.
Найти	функцию		y y(x) ,		удовлетворяющую
уравнению (8.1) и принимающую				при	x a	и x b ( a b )
заданные значения:		y(a)	A;	y(b)	B .
Геометрически это означает, что требуется найти
интегральную кривую уравнения (8.1),					проходящую через
данные точки M1(a, A) и			M 2 (b, B) .

147

Пример. Найти решения уравнения (8.1) y y(x) такое, чтобы y (a) A1 и y (b) B1. Геометрически это означает, что требуется найти интегральную кривую уравнения (8.1),


пересекающую прямые			x	a и	x b	под заданными
углами	и	такими, что tg		A1 ,	tg	B1 .

Замечание 1. Возможна также смешанная краевая задача, когда на одном конце отрезка задается значение функции, на

другом - производной: y(a)		A и y (b)	B1.
Замечание 2. Общая краевая задача (8.1),				(8.2) может:
а)	не иметь решений;
б)	иметь единственное решение;
в)	иметь несколько и даже бесконечно много решений.
В дальнейшем будем предполагать,			что решение краевой
задачи существует и оно единственно.
Методы решения		краевых задач		делятся на

аналитические, численные и приближенные. Аналитические методы изучаются в курсе математического анализа и применимы для узкого класса дифференциальных уравнений. В случае, когда можно найти общее решение дифференциального

уравнения, двухточечная

задача не более сложна, чем задача с

начальными условиями.

Пример. Найти частное решение дифференциального

уравнения

0 ,

удовлетворяющее

краевым условиям:

y(0) 0,

y(1)

Решение.

k 2

1 ; k

y C e x

e x .

1. x1

0 , 0 C1 1 C2 1

2. x

1 C e

e .

Отсюда

следует

-1 + C

C e

e = 1

2sh1

148

y	1	e x	e x	sh x	.

	2sh1			sh1

Однако, если общее решение уравнения не может быть найдено регулярным путем, то решение краевой задачи приводит к новым трудностям, т.к. в отличие от задачи Коши, нет начальной точки, исходя из которой можно было бы построить решение одним из рассмотренных ранее методов.

Приближенные методы дают решение краевой задачи в виде формулы. Ниже будет рассмотрен метод коллокаций.

Численные методы дают решение краевой задачи в виде таблично заданной функции. Рассмотрим некоторые такие численные методы решения краевых задач.

8.2. Метод пристрелки

Так как известно много способов приближенного решения задачи Коши для обыкновенных дифференциальных уравнений, то можно считать краевую задачу решенной, если ее удастся преобразовать к эквивалентной начальной задаче. Известно несколько методов, с помощью которых это можно сделать: метод пристрелки, метод редукции, метод дифференциальной прогонки и т. д. Эти методы приводят к необходимости решать не одну, а несколько задач Коши различной сложности при различных ограничениях на параметры исходной задачи. Рассмотрим один из таких методов, метод пристрелки.

Пусть требуется найти приближенное решение уравнения (в общем случае нелинейного)

f (x, y, y ) , x a,b

(8.3)

с краевыми условиями первого рода

y(a) A, y(b) B .

(8.4)

Зададимся некоторым числом C1 и будем рассматривать задачу Коши для уравнения (8.3) с начальными условиями

149

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 1815 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20223.59 Mб13230.pdf
#
15.11.20223.59 Mб03231.pdf
#
15.11.20223.61 Mб93234.pdf
#
15.11.20223.61 Mб23235.pdf
#
15.11.20223.63 Mб23236.pdf
#
15.11.20223.63 Mб33237.pdf
#
15.11.20223.63 Mб23238.pdf
#
15.11.20223.65 Mб03239.pdf
#
15.11.20223.66 Mб03241.pdf
#
15.11.20223.67 Mб13245.pdf
#
15.11.20223.69 Mб03247.pdf