
3237
.pdf
достаточно гладкой, нет смысла пытаться повышать качество ее полиномиальной аппроксимации за счет многочленов высоких степеней. Более перспективным в этих условиях является применение кусочно-полиномиальной аппроксимации f (x) , предполагающей, что аппроксимирующая функция
(x) составляется из отдельных многочленов, как правило, одинаковой небольшой степени, определенных каждый на своей части отрезка [a,b] . Использование низких степеней многочленов, составляющих (x) , позволяет легко находить
их коэффициенты как из интерполяционных, так и из иных условий.
Так, если заданы значения |
yi |
функции y f (x) на |
|
системе узлов xi таких, что |
|
|
|
a x0 x1 ... |
xn |
b , |
(2.27) |
и требуется аппроксимировать |
f (x) |
кусочно-линейной |
|
функцией (x) , исходя из условий интерполяции
то беря функцию
(x)
(xi ) |
yi , |
(i |
0,1,..., n) , |
|
|
|
(x) в виде |
|
|
|
|
|
|
a1x |
b1 при |
x |
[x0 , x1], |
|
||
a2 x |
b2 |
при |
x |
[x1, x2 |
], |
(2.28) |
.... .... .... .... .... .... |
|
|||||
|
|
|||||
an x |
bn |
при |
x |
[xn 1, xn ], |
|
|
для нахождения n пар ее коэффициентов ak , bk (k 1,2,..., n) имеем систему из 2n линейных уравнений
40

a1x0 |
b1 |
|
y0 , |
|
a1x1 |
b1 |
y1; |
|
|
a2 x1 |
b2 |
|
y1, |
|
a2 x2 |
b2 |
|
y2 ; |
(2.29) |
.... .... .... .... |
|
|||
an xn 1 |
bn |
yn 1, |
|
|
an xn |
bn |
yn , |
|
|
причем, как видим, каждая пара соседних уравнений системы (2.29), имеющих коэффициенты с одинаковыми индексами, не связана с остальными и может решаться отдельно.
Аналогично, каждое звено кусочно-квадратичной
функции (при n |
|
|
2m в (2.27)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
a x 2 |
b x |
c |
|
|
при |
x |
[x |
0 |
, x |
2 |
], |
|
|
|
||||||
|
1 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a |
2 |
x2 |
b x |
c |
2 |
при |
x |
[x |
2 |
, x |
4 |
], |
|
|
|
|||||
(x) |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.... .... .... .... .... .... .... .... |
|
|
|
|
|
|||||||||||||||
|
a |
m |
x2 |
b x |
c |
m |
при |
x [x |
2m 2 |
, x |
2m |
] |
|||||||||
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
||||||||
определяется тройкой коэффициентов ak , bk , ck (k |
1,2,..., n) , |
||||||||||||||||||||
которые могут быть найдены последовательным решением трехмерных линейных систем
a |
k |
x 2 |
b |
k |
x |
2k 2 |
c |
k |
y |
2k 2 |
, |
||||||
|
2k 2 |
|
|
|
|
|
|
|
|
||||||||
a |
k |
x 2 |
b |
|
x |
2k 1 |
c |
k |
|
y |
2k 1 |
, |
(2.30) |
||||
|
2k 1 |
k |
|
|
|
|
|
|
|||||||||
a |
k |
x 2 |
b x |
2k |
|
c |
k |
|
y |
2k |
, |
|
|
|
|
||
|
2k |
k |
|
|
|
|
|
|
|
|
|
|
|||||
соответствующим выставленным интерполяционным условиям.
41
Фактически, в рассмотренных случаях речь идет о
последовательной линейной интерполяции (2.7) |
по |
перемещаемым вдоль отрезка [a,b] парам соседних |
точек |
разбиения (2.27) и о последовательной квадратичной интерполяции (2.8) по тройкам таких точек.
Пример. Для функции y  f (x) , заданной таблицей 6
f (x) , заданной таблицей 6
Таблица 6
x |
0 |
0.5 |
1 |
2 |
3 |
4 |
5 |
f (x) |
1.5 |
0 |
0 |
2 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
выполним простейшие кусочно-линейное и кусочноквадратичное интерполирования.
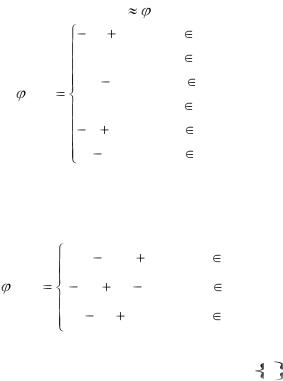
Решение. Проведем линейное интерполирование данной функции на каждом из элементарных промежутков с помощью
формулы (2.28). Положив f (x) |
1(x) , будем иметь |
|||
|
3x |
1.5, |
x |
[0,0.5], |
|
|
0, |
x |
[0.5,1], |
1(x) |
2x |
2, |
x |
[1,2], |
|
0, |
x |
[2,3], |
|
|
|
|||
|
x |
5, |
x |
[3,4], |
|
x |
3, |
x |
[4,5]. |
Квадратичное интерполирование по тройкам известных точек отрезков [0,1] , [1,3] и [3,5] приводит к приближенному равенству
|
3x2 |
4.5x |
1.5, |
x |
[0,1], |
|
2 (x) |
x2 |
5x |
4, |
x |
[1, 3], |
|
|
x2 8x 17, |
x |
[3, 5]. |
|
||
Приведенный |
пример |
приводит к |
|
понятию |
сплайнов. |
|
Пусть отрезок [a,b] |
разбит на n частей точками xi |
: |
||||
42

a x0 |
x1 x2 |
... xi 1 |
xi ... xn |
b. |
Сплайном |
k -й |
степени |
называется |
функция, |
представляющая собой многочлен не выше k -й степени на каждом из последовательно примыкающих друг к другу
интервалов |
(xi 1, xi ) (i |
1,2,..., n |
1) , причем в точках стыка |
|||
двух интервалов |
xi |
(i 1,2,..., n |
1) |
функция |
непрерывна |
|
вместе со |
своими |
производными |
до |
порядка |
не выше k . |
|
Например, непрерывная кусочно-линейная функция (ломаная) является сплайном первой степени с производной, терпящей разрыв в точках излома.
Рассмотрим наиболее известный и широко применяемый интерполяционный сплайн третьей степени (кубический
сплайн). |
|
|
Пусть на отрезке [a,b] |
определена функция y |
f (x) , |
значения которой в точках xi |
равны yi f (xi ) . |
|
Задача интерполяции функции y f (x) на отрезке |
a, b |
|
(сплайном третьей степени) состоит в нахождении функции
S(x) , |
равной многочлену третьей степени |
Si (x) |
на каждом |
|||
отрезке |
xi 1, xi |
(i |
1,2,..., n) , т. е. |
|
|
|
S (x) |
Si (x) |
a0i x3 |
a1i x 2 a2i x a3i , x xi |
1, xi |
, |
(2.31) |
причем значения сплайна в узлах интерполяции |
xi |
равны |
||||
соответствующим значениям заданной функции yi |
и сплайн- |
|||||
функция непрерывна в узлах интерполяции вместе с производными первого и второго порядков
S(xi ) |
Si 1(xi ) yi |
(i |
0,1,2,...n |
1), S(xn ) Sn (xn ) |
yn , (2.32) |
|
Si (xi ) |
Si 1(xi ) |
(i |
1,2,..., n 1), |
(2.33) |
||
Si (xi ) |
Si |
1(xi ) |
(i |
1,2,..., n 1), |
(2.34) |
|
Si (xi ) |
Si |
1(xi ) |
(i |
1,2,..., n |
1). |
(2.35) |
43

Условия |
(2.32) |
- |
(2.35) |
дают |
4n |
2 |
линейных |
алгебраических уравнений для определения 4n |
неизвестных |
||||||
коэффициентов |
aip |
p |
0,1,2,3; |
i |
1,2,..., n |
при |
|
соответствующих степенях x |
в многочленах Si (x) . |
|
|||||
Можно показать, что интерполяционный кубический |
|||||||
сплайн для функции |
y |
f (x) |
существует |
и |
является |
||
единственным, если вместе с уравнениями (2.32)-(2.35)
удовлетворяется |
какая-либо пара дополнительных |
условий |
|||||||
(краевых условий) следующего типа |
|
|
|
|
|||||
I. S (a) |
f (a), |
S (b) |
f (b) ; |
|
|
|
|
||
II. |
S (a) |
f |
(a), |
S (b) |
f (b) ; |
|
|
|
|
III. S (a) |
S (b), |
S (a) |
S (b) . |
|
|
|
|
||
Рассмотрим случай разбиения отрезка |
a, b |
на n |
равных |
||||||
частей |
с |
|
шагом |
|
h , |
для |
|
которого |
|
x0 a, |
x1 x0 |
h, |
xi 1 |
xi |
h,...., xn |
b и |
h |
(b |
a) / n . |
Разберем построение интерполяционного кубического сплайна отдельно для условий I и II типов.
При построении сплайна, удовлетворяющего краевым условиям I типа, введем величины mi S (xi ) , называемые
иногда наклонами сплайна в точках (узлах) |
xi |
(i 0,1,...., n) . |
||||||||||||
Интерполяционный кубический сплайн вида |
|
|
|
|||||||||||
S(x) |
|
Si (x) yi 1 |
(x xi )2 (2(x |
xi 1) h) |
yi |
(x |
xi |
1)2 (2(xi |
x) h) |
|||||
|
|
h3 |
|
|
|
|
|
h3 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+ m |
|
|
(x xi )2 (x xi 1 ) |
+ m |
|
(x xi 1)2 (x xi ) |
, |
(2.36) |
||||||
1 |
|
|
|
i |
|
|
|
|
||||||
i |
|
h2 |
|
|
|
h2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x xi 1, xi |
(i 1,2,..., n) |
|
|
|
|
|||||
удовлетворяет условиям (2.32), |
(2.33), |
(2.34) |
для любых mi . |
|||||||||||
Из условий (2.35) и краевых условий I типа можно определить n 1 параметр mi .
44

Действительно, |
|
|
|
легко |
|
|
|
проверить, |
что |
||||||||||
S (xi 1) |
Si (xi 1) |
|
|
yi 1, |
S (xi ) Si (xi ) |
yi (i 1,2,..., n) . |
|||||||||||||
Кроме того, вычисления показывают, что |
|
|
|
||||||||||||||||
S (xi ) |
Si (xi ) mi , |
|
S (xi ) |
Si |
1(xi ) |
mi , |
(i 1,2,..., n) . |
||||||||||||
Если учесть, что |
|
|
|
|
|
|
|
|
|
|
|||||||||
Si" (xi ) |
2mi |
1 |
|
|
4mi |
|
6 |
yi |
yi |
1 |
|
|
(i |
1,2,..., n |
1) , |
||||
h |
|
|
|
|
h |
|
h2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Si" 1 |
(xi ) |
|
4mi |
|
|
2mi |
1 |
6 |
yi 1 |
|
yi |
|
(i |
1,2,..., n |
1) , |
||||
|
h |
|
h |
|
h2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
а также краевые условия I типа и условия (2.35), то получим систему из n 1 линейных уравнений относительно неизвестных mi
m0 |
b0 |
f (a), |
|
|
|
|
|
mi 1 |
4mi |
mi 1 |
bi |
3( yi 1 |
yi 1) |
(i 1,2, ,..., n |
1) (2.37) |
h |
|
||||||
|
|
|
|
|
|
|
|
mn |
bn |
f (b). |
|
|
|
|
|
Решение этой системы позволяет найти значения |
|||||||
неизвестных |
mi и |
определить |
интерполяционный |
сплайн в |
|||
виде соотношений (2.36).
Матрица А системы (2.36) имеет порядок n 1 и является трехдиагональной
45

1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
4 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
4 |
1 |
0 |
0 |
0 |
|
A |
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
4 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
4 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
Метод Гаусса (метод исключения неизвестных) для системы (2.37) значительно упрощается и носит название метода прогонки. Прямой прогонкой находят так называемые прогоночные коэффициенты
L0 0, |
M 0 |
b0 , |
Li |
|
1 |
|
|
, |
M i |
Li (M i 1 bi ) |
|||||
|
|
|
|
||||||||||||
Li |
1 4 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
(i 1,2,..., n 1) . |
|
|
|||||||
Обратной |
|
прогонкой |
|
последовательно |
определяют |
||||||||||
неизвестные mi |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
mn |
bn , |
|
|
|
|
|
(i |
|
n 1, n |
2,...,0) . |
||||
|
mi |
Li mi |
|
|
M i |
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
||||||
Пример. |
На |
отрезке |
|
0, |
|
|
|
построить |
кубический |
||||||
|
2 |
|
|
||||||||||||
сплайн с шагом |
h |
|
|
, удовлетворяющий на концах отрезка |
|||||||||||
|
2 |
||||||||||||||
краевым |
условиям |
I |
типа и |
интерполирующий функцию |
|||||||||||
y sin x . С помощью интерполяционной формулы вычислить приближенное значение sin 6 и сравнить его с точным.
46

Решение. Будем искать кубическую параболу y S(x) , удовлетворяющую следующим условиям на концах отрезка
x0 |
0 и |
|
|
|
x1 |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y0 |
S (x0 ) |
|
sin x0 |
|
|
0, |
|
|
|
|
y1 |
|
|
S(h) |
sin h |
1, |
|
|
|
|
|||||||||||
m0 |
S (x0 ) |
|
sin |
x0 |
|
cos x0 |
|
|
1, |
|
|
|
|
|
|
|
|
||||||||||||||
m1 |
S (h) |
|
sin h |
|
cos x0 |
|
|
1, |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Подставим значения |
|
h, |
|
y0 , |
y1, m0 , m1 |
в формулу |
||||||||||||||||||||||||
(2.33) и получим сплайн вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
S (x) |
S3 (x) |
|
x2 (2(h |
x) |
|
|
h) |
|
(x |
|
h)2 x |
, |
x |
[0, h]; |
|
|
|
||||||||||||||
|
|
|
|
|
|
h |
3 |
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S (x) |
x |
4( |
3)2 |
|
x |
2 |
4(4 |
|
|
) |
|
x |
3 |
x |
0.057358x |
2 |
0.11074x |
3 |
. |
||||||||||||
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Тогда |
|
sin |
|
|
|
|
S |
|
|
|
|
0.49196983 |
(точное |
значение |
||||||||||||||||
|
|
6 |
|
|
|
6 |
|
|
|||||||||||||||||||||||
равно 0.5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
При |
|
построении сплайна, |
|
удовлетворяющего краевым |
||||||||||||||||||||||||||
условиям |
|
II |
типа, |
|
введем величину |
|
~ |
S (xi ) - значение |
|||||||||||||||||||||||
|
|
|
mi |
||||||||||||||||||||||||||||
второй производной сплайна в узле xi |
|
(i |
0,1,..., n) . |
|
|
||||||||||||||||||||||||||
|
Уравнения (2.32), |
(2.33), |
|
(2.35) |
|
|
будут удовлетворены, |
||||||||||||||||||||||||
если интерполяционный кубический сплайн представить в виде
S(x) Si (x) yi 1 |
(x xi )2 (2(x xi 1) h) |
yi |
(x xi 1)2 (2(xi x) h) |
|
h3 |
h3 |
|||
|
|
~ |
|
(x x)3 |
h2 (x |
i |
x) |
~ |
(x x |
)3 |
h2 |
(x x |
) |
|
|
|
i |
|
|
|
i 1 |
|
|
i 1 |
|
|
|||
+ mi |
1 |
|
|
|
|
|
+ mi |
|
|
|
|
|
, (2.38) |
|
6h |
|
|
|
|
|
6h |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
|
xi |
1, xi |
(i 1,2,..., n) . |
|
|
|
|||
47

Учитывая, что
|
|
|
yi yi |
|
|
|
~ |
|
~ |
|
|
|
||
Si |
(xi ) |
1 |
|
|
hmi |
2hmi |
(i |
1,2,..., n 1) , |
||||||
|
h |
|
|
|
|
|
6 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
yi 1 |
|
yi |
|
|
~ |
~ |
|
|
||
Si 1 |
(xi ) |
|
|
|
2hmi |
hmi 1 |
(i |
1,2,..., n 1) , |
||||||
|
h |
|
|
|
|
|
|
6 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и используя краевые условия II типа и условия (2.34), получим систему из n 1 линейных уравнений относительно
~
неизвестных mi
~
m0 f (a),
~ |
~ |
~ |
6( yi 1 2 yi |
yi 1) |
|
|
mi 1 |
4mi |
mi 1 |
|
|
, (i 1,2,,..., n 1) |
(2.39) |
h2 |
|
|||||
~ |
|
|
|
|
|
|
f (b). |
|
|
|
|
|
|
mn |
|
|
|
|
|
Системы (2.37) и (2.39) являются частными случаями системы линейных алгебраических уравнений следующего вида
u0 |
b0 , |
|
|
|
|
ui 1 |
4ui ui 1 |
bi , |
(i 1,2, ,..., n |
1) |
(2.40) |
un |
bn . |
|
|
|
|
Для |
функции |
f (x) , |
имеющей |
на отрезке |
a, b |
непрерывные производные до третьего порядка включительно,
точность |
интерполяции |
ее кубическим сплайном S(x) |
по |
точкам |
равномерного |
разбиения отрезка с шагом h |
при |
любых указанных ранее краевых условиях оценивается
следующим неравенством для любых |
x на отрезке |
a, b |
|||||||||
|
f (x) S(x) |
|
5 |
M 3h3 |
, где M 3 |
max |
|
f (x) |
|
. |
(2.41) |
|
|
|
|
||||||||
|
|
2 |
|||||||||
|
|
|
|
|
a x b |
|
|
|
|
|
|
Неравенство |
(2.41) |
дает завышенную оценку точности |
|||||||||
приближения функции сплайном в точке.
48

|
2.8. Среднеквадратичное приближение функций. |
||||||
|
|
Метод наименьших квадратов |
|
|
|||
Пусть |
для |
неизвестной |
функции f (x) |
в точках |
|||
x0 , x1 , ..., xm |
экспериментальным путем |
получены |
значения |
||||
y0 |
f (x0 ), |
y1 |
f (x1),...., ym |
f (xm ) . |
|
Интерполяция |
|
позволяет аппроксимировать таблично |
заданную |
функцию |
|||||
f (x) |
с помощью более простой функции |
(x) . |
При этом |
||||
требуется выполнение в узлах интерполяции |
xi |
равенства |
|||||
f (xi ) |
(xi ) |
( i |
0,1,..., m ). В ряде случаев выполнение этого |
||||
условия затруднительно или даже не целесообразно. При большом числе узлов интерполяции степень интерполирующего многочлена получается высокой. Поэтому точность такой аппроксимации гарантирована лишь в небольшом интервале порядка несколько шагов сетки. Для другого интервала приходится заново вычислять коэффициенты интерполяционной формулы. В практических приложениях желательно иметь единую приближенную
формулу f (xi ) |
(xi ) |
( i 0,1,..., m ), пригодную для большего |
отрезка [a,b] . |
При |
этом точность приближения может |
оцениваться по разному. В основу обычно берется рассмотренное отклонение
f (xi )  (xi ) ( i 0,1,..., m ).
(xi ) ( i 0,1,..., m ).
Если требуется малая величина отклонения одной функции от другой во всех точках отрезка, то за меру близости принимают их максимальное отклонение
max |
f (xi ) (xi ) |
|
( i |
0,1,..., m ), |
|
x a,b |
|
|
|
|
|
требуя, чтобы оно было меньше заданного |
0 . В этом |
||||
случае близость между функциями |
f (x) |
и |
(x) называется |
||
равномерной. |
|
|
|
||
49
