
3237
.pdf
|
|
|
y(a) |
|
A, y (a) C1. |
|
|
|
|
|||
Предположим, |
что |
на |
отрезке |
a, b |
|
построено |
||||||
приближенное решение |
y |
y1(x,C1) этой начальной задачи. |
||||||||||
Сравнение значения |
y1(b,C1) |
полученного решения в точке |
||||||||||
x b с заданным, согласно (8.4), значением |
B |
дает |
||||||||||
информацию |
|
для корректирования угла наклона касательной к |
||||||||||
решению y |
|
y2 (x,C2 ) |
новой начальной задачи с условиями |
|||||||||
|
|
|
y(a) |
|
A, y (a) C2 |
|
|
|
|
|||
так, чтобы уменьшить разницу |
B |
y2 (b,C2 ) . Таким образом |
||||||||||
будем задавать значения |
y (a) |
C1, C2 , C3 ,... |
так, чтобы |
|||||||||
обеспечить |
наиболее |
быструю |
сходимость |
к |
числу |
B |
||||||
последовательности |
приближений |
yk (x, Ck ) |
(k |
1,2,3,...) . |
||||||||
Если при заданном |
|
0 |
|
и некотором k |
n будет выполнено |
|||||||
|
|
|||||||||||
неравенство |
B yn (b, Cn ) |
, то за искомое приближенное |
||||||||||
решение краевой задачи |
(8.3)-(8.4) принимается функция |
|||||||||||
y yn (x, Cn ) .Описанный |
|
способ |
получения приближенного |
|||||||||
решения краевой задачи путем последовательного решения нескольких задач Коши для того же уравнения называют методом пристрелки (или стрельбы). Это название следует из геометрической интерпретации этого метода.
8.3. Метод конечных разностей
Идея метода конечных разностей решения краевых задач весьма проста и видна уже из самого названия: вместо производных в дифференциальном уравнении используются их конечноразностные аппроксимации.
Пусть дана линейная краевая задача |
|
y p(x) y q(x) y f (x) |
(8.5) |
с заданными краевыми (граничными) условиями:
150

0 y(a) |
1 y (a) |
A ; |
2 |
2 |
0 ; |
(8.6) |
0 |
1 |
|||||
0 y(b) |
1 y (b) |
B ; |
2 |
2 |
0 . |
(8.7) |
0 |
1 |
|||||
Здесь |
p(x), q(x) |
и |
|
f (x) |
заданные |
функции, |
непрерывные на отрезке |
a, b , |
0 , 1, |
0 , 1 - числа. |
|
||
Данную краевую задачу можно приближенно свести к решению системы алгебраических уравнений путем замены производных конечными разностями. Так как дифференциальное уравнение - линейное и линейны граничные условия, то алгебраическая система будет линейной.
Разобъем отрезок |
a, b |
на n |
равных частей точками |
|||
a x0 , x1,..., xn 1, xn |
b с шагом h : xi |
xi 1 |
h . Обозначим: |
|||
y(xi ) yi ; |
y (xi ) |
yi ; |
y (xi ) |
yi ; |
p(xi ) |
pi ; f (xi ) fi ; |
( i 0,1,..., n ).
|
Рассмотрим задачу (8.5) - (8.7) |
в узле |
x |
xi , |
заменив |
||||||||||
производные кусочно-разностными уравнениями. |
|
|
|
||||||||||||
|
Во внутренних точках отрезка |
a, b : |
|
|
|
|
|
||||||||
yi |
|
yi 1 2 yi |
yi 1 |
; |
yi |
|
yi 1 |
yi 1 |
|
( i |
1,2,..., n |
1 ). |
|||
|
h2 |
|
|
2h |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
На концах отрезка: |
y0 |
y1 y0 |
|
и yn |
yn |
yn 1 |
. |
|||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
h |
|
|
|
|
h |
|
|
|
Тогда во внутренних точках отрезка, дифференциальное уравнение (8.5) заменяется системой линейных алгебраических уравнений (8.8), а граничные условия - уравнениями (8.9):
yi 1 2 yi |
yi 1 |
+ pi |
yi 1 |
yi 1 |
qi yi |
fi ( i 1,2,..., n 1 ), (8.8) |
h2 |
|
|
2h |
|||
|
|
|
|
|
151

0 y0 |
1 |
|
y1 |
|
y0 |
A |
|
|
|
h |
|
|
|||
|
|
|
|
|
|
(8.9) |
|
|
|
|
yn |
|
yn 1 |
||
0 yn |
1 |
|
|
B. |
|||
|
|
|
h |
||||
|
|
|
|
|
|
||
Таким образом, |
получена линейная система ( n 1 ) |
||||||
уравнений с n 1 неизвестными y0 , y1,..., yn . Эти неизвестные - значения искомой функции y(x) в точках x0 ,x1,..., xn .
Решив эту систему, если это возможно, значение искомой функции получим в виде таблицы. В этом заключается метод конечных разностей для линейной краевой задачи.
Пример. Найти решение дифференциального уравнения
y |
|
1 |
y |
3x |
|
на |
отрезке |
1;2 |
|
|
|
с |
шагом |
h |
0.25 |
при |
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
условиях: y(1) |
2, |
y(2) 9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Решение. |
В нашем случае: |
n |
4 ; |
x0 |
1.00 ; |
x1 1.25 ; |
||||||||||||||||||||||||
x2 |
1.50 ; |
|
x3 |
|
1.75; |
|
|
|
x4 |
2.00 ; |
|
|
h2 |
|
1 |
; |
2h |
|
1 |
; |
|||||||||||
|
|
16 |
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y0 |
|
2 ; y4 |
9 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Составим систему (8.8), полагая поочередно |
i 1, 2, 3: |
|||||||||||||||||||||||||||
|
|
|
|
|
y2 |
2 y1 |
y0 |
|
|
|
1 y2 |
y0 |
|
3x1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
h2 |
|
|
|
|
x1 |
|
|
|
2h |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
y3 |
2 y2 |
y1 |
|
|
|
1 y3 |
y1 |
3x2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
h2 |
|
|
|
x2 |
|
|
|
2h |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
y4 |
2 y3 |
y2 |
|
|
|
1 y4 |
y2 |
|
3x3 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
h2 |
|
|
|
|
x3 |
|
|
|
2h |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
16( y2 |
2 y1 |
|
y0 ) |
1.6( y2 |
y0 ) |
3.75 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
16( y3 |
2 y2 |
|
y1) |
1.333( y3 |
|
y1) |
4.50 |
|
|
|
|
||||||||||||||||
|
|
|
|
16( y4 |
2 y3 |
|
y2 ) |
|
1.143( y4 |
y2 ) |
5.25 |
|
|
|
|
||||||||||||||||
152

Добавляя граничные условия (система 8.9) получим систему пяти уравнений с пятью неизвестными:
y0 2
17.6 y0 32y1 14.4 y2 3.75
17.33y1 32y2 14.667y3 4.50 . 17.143y2 32y3 14.857y4 5.25
y4 9
Отсюда следует
32y1 14.4 y2  31.75
31.75
17.33y1 32y2 14.667y3 4.50  17.143y2 32y3
17.143y2 32y3  128.463
128.463
y1 |
0.45 y2 |
|
0.983 |
y1 |
1846. y2 |
0.846 y3 |
0.260 |
|
y2 |
1867. y3 |
7.494 |
y1 |
0.45 y2 |
|
0.983 |
|
1396. y2 |
0.846 y3 |
0.723 |
|
y2 |
1867. y3 |
7.494 |
y1 |
0.45 y2 |
|
0.983 |
|
y2 |
0.606 y3 |
0.518 |
|
y2 |
1867. y3 |
7.494 |
y1 |
0.45 y2 |
|
0.983 |
|
y2 |
0.606 y3 |
0.518 . |
|
|
1261.y3 |
8.012 |
153

|
Далее, |
|
последовательно |
находим |
y3 6.354 , |
|||||
y2 |
4.368, |
y1 2.949. |
|
|
|
|
|
|||
|
Решение получено в виде таблицы 23: |
|
|
|||||||
|
|
|
|
|
|
|
Таблица 23 |
|
||
|
|
|
1.00 |
|
1.25 |
1.50 |
1.75 |
|
2.00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.00 |
|
2.949 |
4.368 |
6.354 |
|
9.00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
большом |
n непосредственное решение системы |
|||||||
(8.8), |
(8.9) |
становится затруднительным. |
|
|
||||||
8.4. Решение линейной краевой задачи методом прогонки
При решении линейной краевой задачи (8.5) - (8.7) для дифференциального уравнения второго порядка методом конечных разностей получается трехчленная система алгебраических уравнений, каждое из которых связывает не более трех неизвестных.
yi 1 |
2 yi yi 1 |
+ pi |
yi 1 |
yi 1 |
qi yi |
fi ,(i 1,2,..., n 1) |
|||||
|
h2 |
|
|
2h |
|||||||
|
|
|
|
|
|
|
|
||||
0 y0 |
1 |
|
y1 |
y0 |
A |
|
|
|
|||
|
|
h |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
0 yn |
1 |
|
yn |
yn 1 |
|
B. |
|
|
|
||
|
|
h |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Проведем в данной системе группировку неизвестных:
154

1 |
|
|
pi |
yi |
|
1 |
|
|
|
|
2 |
|
qi |
|
|
yi |
1 |
|
|
pi |
yi 1 |
fi ,(i 1,2,..., n |
|
1) |
||||||||||||||
|
h2 |
|
|
2h |
|
|
|
|
|
|
h2 |
|
|
|
|
h2 |
|
|
2h |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
1 |
|
y |
0 |
|
1 |
|
y |
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
h |
|
|
|
h |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
1 |
|
yn |
|
|
1 |
|
|
yn 1 B. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
h |
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Два |
последних |
|
равенства умножим на h , |
а остальные - |
||||||||||||||||||||||||||||||||
на h2 и переобозначим коэффициенты уравнения: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
b |
|
h |
|
|
; |
|
|
|
|
|
|
|
c |
|
|
|
|
; |
|
|
|
|
Ah ; |
|
|
a |
|
1 |
|
1 |
p |
h ; |
||||||
0 |
1 |
|
|
|
|
|
|
|
0 |
1 |
|
|
0 |
|
|
|
i |
|
|
|||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
i |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b q h2 |
2 ; |
|
|
|
|
|
|
c 1 |
|
1 |
p h ; |
|
|
|
f |
h2 |
; |
|
|
a |
|
|
|
|
; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
n |
|
1 |
|||||||||||||||||||||||
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
2 |
|
i |
|
|
i |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
bn |
0h |
|
1 ; |
|
n |
|
|
Bh . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Тогда система запишется в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
b0 y0 |
|
|
c0 y1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
ai yi 1 |
|
|
bi yi |
|
ci yi |
1 |
|
|
i , |
|
( i |
1,2,..., n |
|
1 ) . |
(8.10) |
|||||||||||||||||||
|
|
|
|
an yn 1 |
|
bn yn |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Матрица этой системы (и сама система) является трехдиагональной. Такие системы выгодно решать методом прогонки. Поэтому и весь метод решения краевой задачи (8.5)- (8.7), сведенной к системе (8.10), называется методом прогонки.
Если решить систему (8.10) предыдущего примера методом прогонки, то получим таблицу 24:
Таблица 24
1.00 |
1.25 |
1.50 |
1.75 |
2.00 |
|
|
|
|
|
2.00 |
2.948 |
4.367 |
6.351 |
8.00 |
|
|
|
|
|
155

т.е., полученное решение отличается от предыдущего в третьих знаках после запятой, что связано со спецификой округления при различных способах решения алгебраической системы.
Так как исходный отрезок 1;2 был разбит на малое
был разбит на малое
число частей ( n 4 ), то оба решения значительно отличаются (уже вторыми знаками после запятой) от точного решения.
Замечание. Вообще с помощью конечно-разностных методов трудно получить решение с большей степенью точности. Для повышения точности приходится применять более громоздкие приемы или вводить соответствующие поправки. Один из путей - использование более точных формул для производных, в первую очередь, для односторонних производных в граничных условиях.
8.5. Решение линейной краевой задачи методом коллокаций
В отличие от метода конечных разностей, являющегося численным, метод коллокаций относится к приближенным методам. Он позволяет найти приближенное решение краевой задачи в виде аналитического выражения.
Пусть надо решить линейную краевую задачу на отрезке a; b :
y p(x) y
p(x) y q(x) y
q(x) y 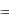 f (x) ;
f (x) ;
0 y(a) |
1 y (a) |
A ; |
( |
0 y(b) |
1 y (b) |
B ; |
( |
2 |
2 |
0 ); |
|
0 |
1 |
||
|
|||
2 |
2 |
0 ). |
|
0 |
1 |
||
|
Для кратности записи будем использовать обозначения:
L y y p(x) y q(x) y ; y |
0 y(a) 1 y (a) ; |
y 0 y(b)
0 y(b)  1 y (b) .
1 y (b) .
Выберем некоторую систему линейно независимых (базисных) функций:
156

|
|
u0 (x); u1 (x); u2 (x);...; un (x) . |
|
|
|
|
(8.11) |
||||||||
При этом функция |
u0 (x) |
удовлетворяет неоднородным |
|||||||||||||
граничным условиям (8.6), |
(8.7): |
|
|
|
|
|
|
|
|||||||
|
|
Г a u0 |
A ; |
|
Гb u0 |
B , |
|
|
|
|
(8.12) |
||||
а все остальные |
функции |
|
удовлетворяют |
однородным |
|||||||||||
граничным условиям: |
|
|
|
|
|
|
|
|
|
|
|||||
|
Г a ui |
0 ; |
Гb ui |
0 |
( i |
1,2,..., n ). |
(8.13) |
||||||||
Замечание |
1. |
Если |
граничные условия |
(8.6), |
(8.7) |
||||||||||
однородные, т.е. A |
0 , |
|
B |
0 , |
|
то u(x) |
|
0 |
и |
вместо |
|||||
системы |
функций (8.11) |
рассматривается система функций: |
|||||||||||||
u1 (x); u2 (x);...; un (x) . |
|
|
|
|
|
|
|
|
|
|
|||||
Замечание 2. Система n |
функций |
1 (x); 2 (x);...; n (x) |
|||||||||||||
называется линейно |
зависимой |
на множестве |
X , |
если |
|||||||||||
существуют |
n |
|
таких |
постоянных (среди которых хотя бы |
|||||||||||
одна отлична от нуля), что равенство |
|
|
|
|
|
|
|||||||||
|
|
c1 1 (x) |
c2 |
2 (x) ...cn n (x) 0 |
|
|
|
|
|||||||
выполняется тождественно, т.е. |
для |
x |
|
X . |
Если же |
||||||||||
указанное |
равенство возможно лишь при условии, |
что все |
|||||||||||||
коэффициенты |
|
ci |
0 , |
|
то |
система функций |
называется |
||||||||
линейно независимой на отрезке множества X . |
|
|
|
|
|||||||||||
Достаточным |
условием |
линейной |
независимости |
||||||||||||
функций |
на |
множестве |
X |
|
является |
отличие от нуля |
|||||||||
определителя Вронского: |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 (x) |
|
|
2 (x) ... |
n (x) |
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
W (x) |
|
|
1 (x) |
|
|
21 (x) ... |
n (x) |
. |
|
|||||
|
|
|
... |
|
|
... |
|
... |
... |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
(n 1) (x) |
(n 1) (x) ... |
(n 1) |
(x) |
|
|
||||||
|
|
|
|
1 |
|
|
2 |
|
|
|
n |
|
|
|
|
157

Будем искать приближенное решение краевой задачи (8.5) - (8.7) в виде линейной комбинации базисных функций:
|
n |
|
yn u0 (x) |
ciui (x) . |
(8.14) |
i 1
Эта функция удовлетворяет граничным условиям (8.6) и (8.7). Действительно, в силу линейности граничных условий имеем:
|
|
|
|
n |
|
|
|
n |
|
Г a yn |
Г a u0 (a) |
|
ciui (a) |
Г a u0 |
Г a |
ciui (x) |
|||
|
|
|
|
i 1 |
|
|
|
i 1 |
|
|
|
|
n |
|
n |
|
|
|
|
Г a u0 |
|
ci Г a ui |
A |
ci 0 A, |
|
|
|||
|
|
i |
1 |
|
i 1 |
|
|
|
|
т.е. Г a |
yn |
A . Аналогично, Гb |
yn |
B . |
|
|
|||
Подставим функцию (8.14) в уравнение (8.5) |
|
||||||||
|
|
|
n |
|
|
|
n |
|
|
|
yn |
u0 (x) |
ciui (x) ; |
yn |
u0 (x) |
ciui (x) , |
|||
|
|
|
i |
1 |
|
|
|
i 1 |
|
получим |
|
|
|
|
|
|
|
|
|
u0 (x) |
p(x)u0 (x) q(x)u0 (x) |
|
|
|
|||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
ci ui (x) |
p(x)ui (x) q(x)ui (x) |
f (x). |
||||
|
|
|
i 1 |
|
|
|
|
|
|
Так как |
yn (x) |
не является точным решением краевой |
|||||||
задачи, |
то |
данное равенство не будет тождеством. Перенося |
|||||||
f (x) |
в левую часть равенства, |
получим так |
называемую |
||||||
невязку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
R(x, c1, c2 ,..., cn ) |
L u0 |
|
ci L ui |
f (x) . |
(8.15) |
|||
|
|
|
|
|
|
i 1 |
|
|
|
158

Невязка - функция от x |
и параметров c1,c2 ,..., cn . Если |
|||||
бы x1,x2 ,..., xn |
была точным решением краевой задачи, то |
|||||
R(x, c1, c2 ,..., cn ) |
0 |
x |
a; b . |
|
|
|
При |
приближенном |
решении |
краевой |
задачи |
||
коэффициенты |
ci |
стараются подобрать так, чтобы невязка |
||||
была минимальной. В зависимости от способа нахождения этих коэффициентов и получают различные приближенные методы.
Вметоде коллокаций на отрезке a; b выбирают
достаточно густую систему точек x1,x2 ,..., xn , называемых
точками коллокаций, и требуют, чтобы в этих точках невязка обращалась в нуль. В качестве этих точек можно брать любые
точки отрезка. |
Можно |
брать, например, точки, делящие |
||||
отрезок |
a; b на равные |
части. В результате получим систему |
||||
линейных |
алгебраических |
уравнений относительно |
||||
коэффициентов |
ci : |
|
|
|
|
|
|
|
R(x1, c1, c2 ,..., cn ) |
0 |
|
||
|
|
R(x2 |
, c1, c2 |
,..., cn ) |
0 |
(8.16) |
|
|
.......... .......... .......... ... |
|
|||
|
|
|
|
|||
R(xn , c1, c2 ,..., cn ) 0.
Если полученная система совместна, то из нее находят коэффициенты c1,c2 ,..., cn и подставляют их в формулу (8.14),
которая и дает приближенное решение задачи на отрезке a; b .
Основная трудность использования данного метода состоит в выборе системы базисных функций (8.11).
Пример. |
Методом коллокаций |
решить краевую задачу |
|||
y (1 |
x2 ) y 1 0 , |
y( 1) |
0, y(1) |
0 . |
|
Решение. |
В качестве базисной системы берем функции |
||||
un (x) |
x2n 2 (1 |
x2 ) , |
( n |
1,2,... ). Очевидно, что при любом |
|
159
