3237
.pdf
un,k |
2 (tk ) , |
k 0,1,2,..., m . |
Для аппроксимации частных производных второго порядка рассматриваемой задачи шаблон изображен на рис.20, из которого видно, что полученная схема является неявной.
Рис. 20
Запишем разностное уравнение следующим образом
c 2 |
ui 1,k 1 1 |
2c 2 |
ui,k 1 |
c 2 |
ui 1,k 1 ui,k f (xi , tk 1 ) . (9.14) |
|
h2 |
h2 |
h2 |
||||
|
|
|
Схема (9.14) аппроксимирует уравнение (9.11) только во внутренних узлах сетки, поэтому число уравнений в схеме (9.14) меньше числа неизвестных ui,k . Недостающие
уравнения получаем из граничных условий |
|
|
||
u0,k |
1(tk ) , |
un,k |
2 (tk ) . |
(9.15) |
Схема (9.14)-(9.15) неявная, поэтому значения |
ui,k |
|||
находят как решение |
системы |
линейных уравнений (9.14). |
||
Для решения этой системы можно применять любой алгоритм решения систем линейных уравнений, однако она обладает трехдиагональной матрицей и рациональнее всего решать ее
методом прогонки. Таким |
образом, последовательно |
|
170 |
проходя все слои t |
k , начиная с нулевого слоя, для которого |
|
известны значения |
ui,0 |
(xi ) , находим сеточную функцию |
ui,k , значения которой в узлах сетки приближенно заменяют
значения искомого решения исходного уравнения. Замечательным свойством неявной схемы (9.14) является
ее устойчивость при любых значениях 
h2 0 . Явная схема оказывается устойчивой только при 
h2 
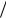2 . Это означает, что вычисления по явной схеме придется вести с очень малым шагом по 
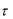, что может привести к большому числу вычислений. В неявной схеме вычисления на одном шаге требуют больше операций, но зато величину шага 
можно выбрать как угодно большой без риска нарушить устойчивость системы. Все это позволяет сократить число вычислений. Для получения точного решения следует проводить дробление шага.
Задачи для самостоятельного решения
1.Используя метод сеток, составить приближенное
решение |
задачи |
|
|
Дирихле |
для |
уравнения |
Лапласа |
||||||||||||||||||
|
2u |
|
|
2u |
|
0 |
в |
квадрате ABCD , где |
функция |
u u(x, y) |
|||||||||||||||
|
x 2 |
y 2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
задана |
на |
сторонах |
квадрата |
уравнениями: |
AB : u 0 ; |
||||||||||||||||||||
|
BC : u 50x(1 x); |
CD : u 50y(1 y2 ) ; AD : u 50x(1 x) . |
|
||||||||||||||||||||||
2. |
Используя |
метод |
сеток, |
составить |
решение |
||||||||||||||||||||
дифференциального |
уравнения |
Лапласа |
2u |
|
2u |
0 |
с |
||||||||||||||||||
x 2 |
y 2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
заданными начальными условиями; шаг h 1. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
x2 |
|
|
y 2 |
|
1 (Г ) , |
u(x, y) Г |
|
x |
|
|
y |
|
. |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
9 |
16 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
171 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. Используя метод сеток, составить решение смешанной задачи для дифференциального уравнения параболического
типа |
u |
|
2u |
(уравнение теплопроводности) при заданных |
|||||
t |
x2 |
||||||||
|
|
|
|
|
|
||||
начальных |
условиях |
u(x,0) 3x(2 |
x) , |
u(0,t) |
0 , |
||||
u(0.6,t) t |
2.52. Решение выполнить |
при |
h 0.1 |
для |
|||||
t0;0.01 .
4.Используя метод сеток, составить решение смешанной
задачи |
|
для уравнения колебания |
струны |
2u |
|
2u |
с |
|||
|
t 2 |
x2 |
||||||||
|
|
|
|
|
|
|
|
|||
начальными условиями u(x,0) |
2x(x |
1) |
0.3, ut (x,0) |
2 sin x |
||||||
(0 |
x |
1) и краевыми условиями u(0,t) |
0.3, u(1,t) |
t 4.3 . |
||||||
Решение |
выполнить с шагом |
h |
0.1 , |
определяя значения |
||||||
функции |
u(x,t) с четырьмя десятичными знаками, |
причем |
||||||||
0 |
t |
0.5. |
|
|
|
|
|
|
|
|
172
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Амосов А.А. Вычислительные методы для инженеров / А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова – М: Высш.
шк., 1994. 544 с.
2.Бахвалов Н.С. Численные методы / Н.С. Бахвалов, Н.О. Жидков, Г.Н. Кобельков – М: Высш. шк., 1987. 518 с.
3.Вержбицкий В.М. Численные методы / В.М. Вержбицкий - М: Высш. шк., 2001. 382 с.
4.Воробьев Г.Н. Практикум по вычислительной математике / Г.Н Воробьев, А.Н. Данилова – М: Высш. шк.,
1990. 208 с.
5.Демидович Б. П. Основы вычислительной математики / Б. П. Демидович, И.А. Марон – М: Наука, 1970. 664 с.
6.Гутер Р.С. Элементы численного анализа и
математической |
обработки результатов опыта / Р.С. Гутер, |
|
Б.В. Овчинский – |
М: Наука, 1970. 432 с. |
|
7. Копченова Н.В. Вычислительная математика |
в |
|
упражнениях и задачах / Н.В. Копченова, Марон И.А. – |
М: |
|
Наука, 1972.. |
|
|
8. Ракитин В.И. Практическое руководство по методам вычислений с приложением программ для персональных компьютеров / В.И Ракитин, В.Е. Первушин – М: Высш. шк.,
1998. 376 с.
9. Плис А.И. Лабораторный практикум по высшей математике / А.И Плис, Н.А. Сливина – М: Высш. шк., 1994.
206 с.
10. Турчак Л.И. Основы численных методов / Л.И. Турчак
– М: Наука, 1982. 318с.
173
ОГЛАВЛЕНИЕ
Введение ..…………………………………………………..3
1.Действия над приближенными числами ... ..…………...4
1.1.Основные источники погрешностей……..…….……....4
1.2.Приближенные числа. Абсолютная и относительная погрешности …………………………………………….5
1.3.Правила записи приближенных чисел……………......10
2.Методы аппроксимации функций ………………………15
2.1.Постановка задачи аппроксимации...…………………15
2.2.Вычисление значений многочлена по схеме Горнера 16
2.3.Постановка задачи интерполирования. Локальная и глобальная интерполяция ……………………………..18
2.4.Интерполяционный многочлен Лагранжа ……….…..22
2.5.Конечные разности………………………………….....27
2.6.Интерполяционные многочлены Ньютона…………...30
2.7.Интерполирование функции кубическими сплайнами
………………………………………………………….37
2.8.Среднеквадратичное приближение функций. Метод наименьших квадратов………………………………..49
3.Численные методы линейной алгебры ……...………...55
3.1.Линейные системы уравнений ..……………...............55
3.2.Метод исключения Гаусса.……………………….........55
3.3.Определитель и обратная матрица .…………………..61
3.4.Итерационные методы .……………………………….67
3.5.Понятие о методе Зейделя …………………………….74
4.Решение нелинейных уравнений и систем…………...79
4.1.Общие замечания .………………..…….……………79
4.2.Нахождение действительных корней уравнения……79
4.3.Метод деления отрезка пополам…………………....82
174
4.4.Метод простых итераций ..……....………………….85
4.5.Метод Ньютона ………..…………………………….89
4.6.Метод хорд…………………………………………….93
4.7.Комбинированный метод…………………………….96
4.8.Решение нелинейных систем методом Ньютона……98
4.9.Метод итерации для системы двух уравнений…….100
5.Численное дифференцирование …………………… 105
5.1.Постановка вопроса …………………………………105
5.2.Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона …...……………….......................................107
5.3.Конечно-разностные аппроксимации производных
…………………………………………………………111
6.Численное интегрирование ………....…........................114
6.1.Постановка задачи……….....………………………..114
6.2.Метод прямоугольников ……………………………115
6.3.Метод трапеций…….. ..……………………………...117
6.4.Параболическая интерполяция. Формула Симпсона
…………………………………………………………122
6.5.Правило Рунге оценки погрешности………………...127
6.6.Квадратурная формула Гаусса …………………….128
7.Численное решение обыкновенных дифференциальных уравнений ……………..……….…………………………133
7.1.Понятие о численном решении задачи Коши…………....133
7.2.Метод последовательных приближений…………...135
7.3.Метод Эйлера………………………………................137
7.4.Исправленный метод Эйлера………………………140
7.5.Метод Рунге-Кутта…………………………………...142
8.Краевые задачи для обыкновенных дифференциальных уравнений..……………….……………………………….147
175
8.1.Постановка задачи ……………..……………...........147
8.2.Метод пристрелки…………………………………...149
8.3.Метод конечных разностей ………………………..150
8.4.Решение линейной краевой задачи методом прогонки
...………………………………………………….……154
8.5.Решение линейной краевой задачи методом коллокаций……………………………………………156
9.Численное решение дифференциальных уравнений в частных производных ………….……………….……...162
9.1.Решение задачи Дирихле для уравнения Лапласа методом сеток ……….………..……………………...162
9.2.Решение смешанной задачи для уравнения гиперболического типа методом сеток …………….165
9.3.Решение смешанной задачи для уравнения параболического типа методом сеток ……………...168
Библиографический список ……….………..…………173
176
Учебное издание
Бырдин Аркадий Петрович Заварзин Николай Владимирович Сидоренко Александр Алексеевич Цуканова Людмила Петровна
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА
В авторской редакции
Подписано к изданию 23.10.2012. Уч.-изд. л. 11,0.
ФГБОУ ВПО “Воронежский государственный технический университет”
394026 Воронеж, Московский просп., 14
177