
3177
.pdf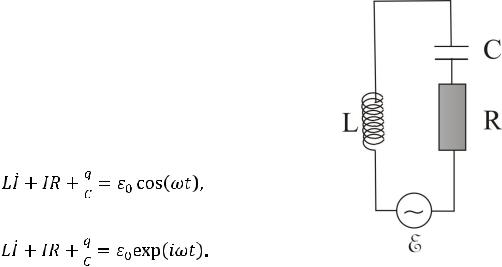
К о н т р о л ь н ы е в о п р о с ы и у п р а ж н е н и я
1.За 1 мин амплитуда затухающих колебаний уменьшается в 4 раза. Во сколько раз она уменьшится за 1,5 мин?
2.За 1 мин энергия затухающих колебаний уменьшается в 4 раза. Во сколько раз она уменьшится за 1,5 мин?
3.За 1 мин амплитуда затухающих колебаний уменьшается в 4 раза. Во сколько раз уменьшится их энергия за 1,5 мин?
4.Колебательный контур состоит из сопротивления в 1 Ом, индуктивности в 0,001 Гн и конденсатора емкостью в 10-6 Ф. Определить частоту колебаний, время затухания и добротность контура.
Глава 13. Вынужденные колебания. Резонанс
Во всякой реальной колебательной системе возникающие за счет первоначального толчка колебания вследствие диссипации энергии с течением времени затухают. Чтобы поддерживать в системе незатухающие колебания, необходимо компенсировать потерю энергии за счет внешних источников. Если эта компенсация происходит периодически, возникают вынужденные колебания. Простейшим случаем периодического внешнего воздействия является гармоническое воздействие.
ВЫНУЖДЕННЫЕ ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ.
Схема цепи, в которой возникают вынужденные электрические колебания, содержит сопротивление R, катушку индуктивности L, конденсатор С и источник переменной ЭДС ε с гармонической зависимостью ее величины от времени (рис. 13.1).
Закон Ома для замкнутой цепи в этом случае имеет вид
|
|
|
|
(13.1) |
|
|
|
|
|
||||
или в комплексной форме |
|
|||||
|
|
(13.2) |
Рис. 13.1. Схема |
|||
|
||||||
Общее решение неоднородного уравнения |
||||||
последовательного |
||||||
(13.2) равно сумме общего решения соответствую- |
||||||
колебательного контура |
||||||
щего однородного уравнения и частного решения |
||||||
с источником |
||||||
неоднородного уравнения. Физически это означает, |
||||||
переменной ЭДС |
||||||
что колебания системы представляют собой наложе- |
|
|||||
ние ее свободных колебаний с собственной частотой, определяемой однородным уравнением, и колебаний под действием внешней силы. Однородное урав-
81
нение, соответствующее (13.2), есть уравнение затухающих колебаний, и его решение уже получено в предыдущей главе. Запишем его в комплексном виде:
(13.3)
где |
|
|
|
(13.4) |
|
|
Далее будем искать частное решение неоднородного уравнения в комплексной форме:
(13.5)
Подставив (13.5) в (13.2) и учитывая, что 1/i = -i, получим
(13.6)
Здесь использованы правила дифференцирования и интегрирования экспоненциальных функций вида (13.5). Сокращая множитель exp(iωt) в обеих частях равенства, преобразуем соотношение (13.6) к виду
(13.7)
откуда получаем комплексную амплитуду тока
(13.8)
Таким образом, полное решение дифференциального уравнения вынужденных колебаний содержит два слагаемых:
1)затухающее со временем слагаемое вида (13.3);
2)незатухающее со временем слагаемое (13.5), амплитуда которого (13.8) не зависит от времени.
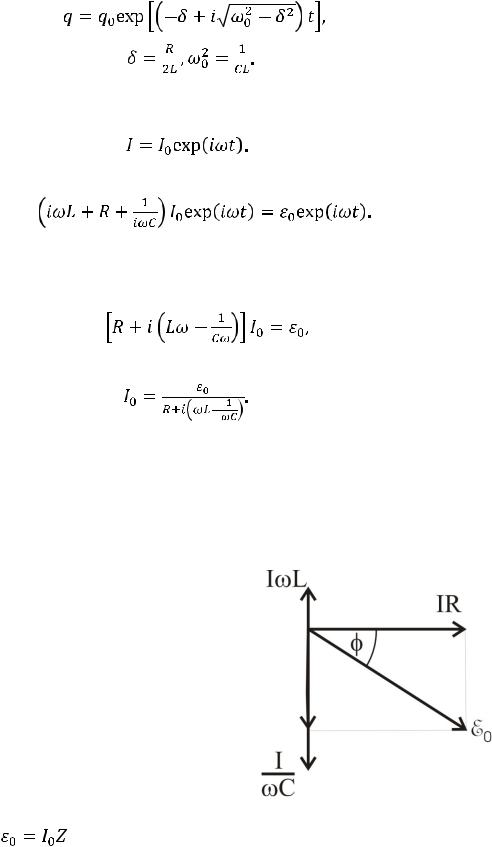
Режим колебаний, при котором необходимо учитывать оба слагаемых, называется переходным. Время релаксации большинства реальных систем мало, и их поведение довольно быстро становится практически стационарным. Векторная диаграмма для стационарных колебаний в контуре приведена на рис. 13.2. Коэффициент пропорциональности Z между током и ЭДС, играющий для переменного тока ту же роль, что и сопротивление для постоянного тока, называется импедансом, а выраженное через Z соотношение между ЭДС и током
(13.9)
носит название закона Ома в комплексной форме.
Рис. 13.2. Векторная диаграмма вынужденных
электрических колебаний
82

В соответствии с (13.7) импеданс следующим образом выражается через параметры цепи и частоту:
(13.10)
Комплексную величину Z можно представить в виде
(13.11)
где |
|
|
|
|
|
(13.12) |
|
|
|
|
|
||
|
|
|
|
(13.13)
Формула (13.13) определяет начальную фазу тока. Модуль амплитуды тока
(13.14)
а разность фаз между ЭДС и током в цепи совпадает с фазой импеданса θ.
РЕЗОНАНС НАПРЯЖЕНИЙ. Как видно из уравнения (13.14), амплитуда силы тока в цепи существенно зависит от частоты ω внешней вынуждающей силы и
имеет максимум |
|
|
|
при выполнении для частоты условия |
|
|
|
||
|
|
|
|
|
(13.15)
Явление, заключающееся в резком возрастании амплитуды вынужденных колебаний силы тока при стремлении частоты внешней силы к фиксированному значению ωr, называется резонансом напряжений. Из уравнения (13.15) следует формула Томпсона для величины резонансной частоты:
(13.16)
Таким образом, резонанс напряжений наблюдается при совпадении частоты внешней вынуждающей силы с собственной частотой идеализированного контура с сопротивлением R = 0. Высота и ширина резонансного максимума зависят от величины активного сопротивления. Графики зависимости амплитуды тока от частоты при различных активных сопротивлениях приведены на рис. 13.3.
Как следует из уравнения (13.14), в точке резонанса импеданс действителен и совпадает с активным сопротивлением: Z = R. С другой стороны, в соответствии с (13.13)
(13.17)
и, следовательно, сдвиг фаз между током и ЭДС равен нулю: θr = 0. Этот факт делает понятной физическую причину возрастания амплитуды тока в резонансе. Поскольку в резонансе ток и ЭДС находятся в одной фазе, то нет моментов времени, в которые ЭДС противодействует возрастанию тока.
83
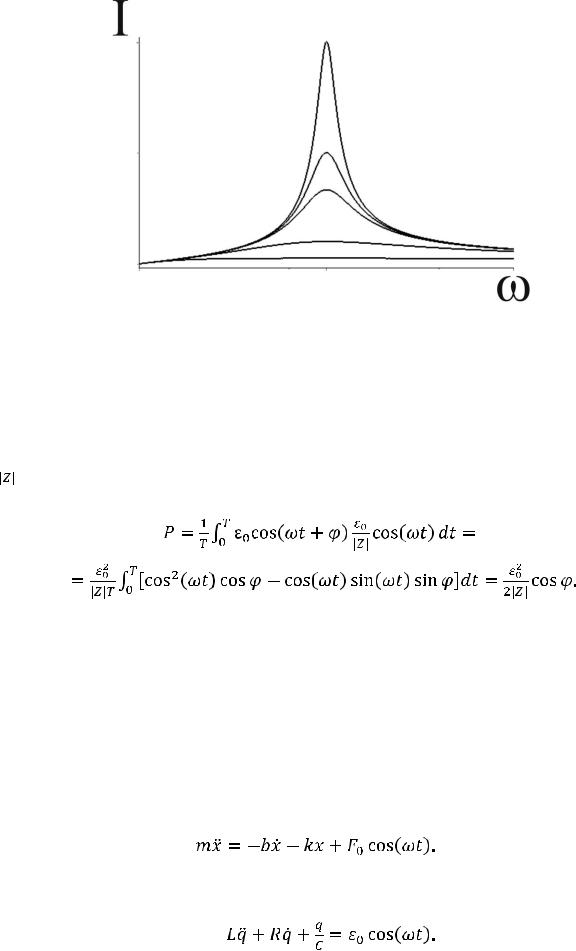
Рис. 13.3. Резонансные зависимости силы тока от частоты
МОЩНОСТЬ, ВЫДЕЛЯЮЩАЯСЯ В ЦЕПИ ПЕРЕМЕННОГО ТОКА. Покажем, что в
резонансе система наиболее эффективно поглощает энергию из внешнего источника. Мгновенная мощность, выделяющаяся в колебательном контуре, равна произведению мгновенной ЭДС ε0cos (ωt + θ) на мгновенное значение тока

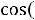
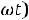 . Средняя мощность Р за период Т есть интеграл от мгновенной мощности, деленный на период:
. Средняя мощность Р за период Т есть интеграл от мгновенной мощности, деленный на период:
(13.18)
Таким образом, максимальная мощность выделяется при θ = 0, что соответствует условию резонанса напряжений. В реальных электрических цепях большая часть реактивной нагрузки является индуктивной. Для увеличения величины cosθ в цепи ставят конденсаторы большой емкости.
ВЫНУЖДЕННЫЕ МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ. По аналогии с электриче-
скими колебаниями нетрудно рассмотреть и вынужденные механические колебания с учетом затухания. Уравнение движения механического осциллятора при наличии внешней гармонической силы с амплитудой F0 и частотой ω имеет вид
(13.19)
Аналогом этого уравнения является уравнение (13.1), переписанное через функцию q.
(13.20)
84

Поскольку уравнение (13.1) решалось относительно функции тока 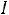
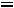
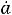 , все сделанные ранее выводы относительно зависимости силы тока от частоты теперь справедливы для скорости
, все сделанные ранее выводы относительно зависимости силы тока от частоты теперь справедливы для скорости 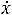 после замен
после замен
(13.21)
В частности, импеданс механического осциллятора равен
(13.22)
и, аналогично резонансу токов, положение резонанса скоростей не зависит от сопротивления среды. Физически понятна также причина увеличения амплитуды скорости в резонансе. Поскольку фаза скорости и вынуждающей силы совпадают, внешняя сила всегда увеличивает скорость осциллятора. При не равной нулю разности фаз существуют части периода, когда сила и скорость имеют разные знаки и, следовательно, внешняя сила тормозит осциллятор.
В отличие от резонанса скоростей, положение резонанса смещений зависит не только от массы и коэффициента упругости, но от сопротивления среды:
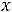
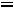
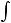
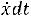 . В результате интегрирования гармонической функции в знаменателе появляется множитель , и экстремум смещения наблюдается при условии
. В результате интегрирования гармонической функции в знаменателе появляется множитель , и экстремум смещения наблюдается при условии
(13.23)
или |
|
(13.24) |
|
Отсюда либо ω = 0, либо резонансная частота
(13.25)
Экстремум =0 является минимумом и соответствует статической силе, не приводящей к вынужденным колебаниям. Из уравнения (13.25) видно, что с увеличением силы трения положение резонанса смещений сдвигается в сторону малых частот. График зависимости амплитуды смещения от частоты приведен на рис. 13.5.
Рис. 13. 5. График зависимости амплитуды смещения от частоты
85
К о н т р о л ь н ы е в о п р о с ы и у п р а ж н е н и я
1.Нарисуйте график зависимости смещения вынужденных колебаний от времени для интервалов времени, меньших времени релаксации.
2.Нарисуйте график зависимости смещения вынужденных колебаний от времени для вынуждающей силы, представляющей собой короткие периодические толчки с периодом, превышающим время релаксации.
3.Нарисуйте векторную диаграмму для скоростей механического осциллятора, движущегося под действием силы с нерезонансной частотой.
4.Нарисуйте векторную диаграмму для скоростей механического осциллятора, движущегося под действием силы с резонансной частотой.
5.Нарисуйте векторную диаграмму для смещений механического осциллятора, движущегося под действием силы с нерезонансной частотой.
Глава 14. Связанные колебания. Нелинейные колебания
До сих пор мы рассматривали поведение изолированных осцилляторов, но в природе осцилляторы редко находятся в полной изоляции. Чаще они взаимодействуют с другими осцилляторами, вследствие чего становится возможным перенос энергии от одной колебательной системы к другой. В том случае, если взаимодействие происходит за счет диссипативных элементов (электрического сопротивления, силы трения и др.), происходит потеря энергии и затухание колебаний. В противоположном случае, если взаимодействие происходит за счет реактивных элементов (емкости, индуктивности, пружины и др.), возможен перенос энергии через большое число осцилляторов. Этот механизм представляет собой основу волнового движения.
ОСЦИЛЛЯТОРЫ, СВЯЗАННЫЕ УПРУГИМИ СИЛАМИ. Рассмотрим два одинако-
вых математических маятника массой m и длиной l, связанных невесомой пружиной с коэффициентом жесткости k. Длина недеформированной пружины равна расстоянию между находящимися в равновесии телами (рис. 14.1).
Рис. 14.1. Система двух связанных маятников
86
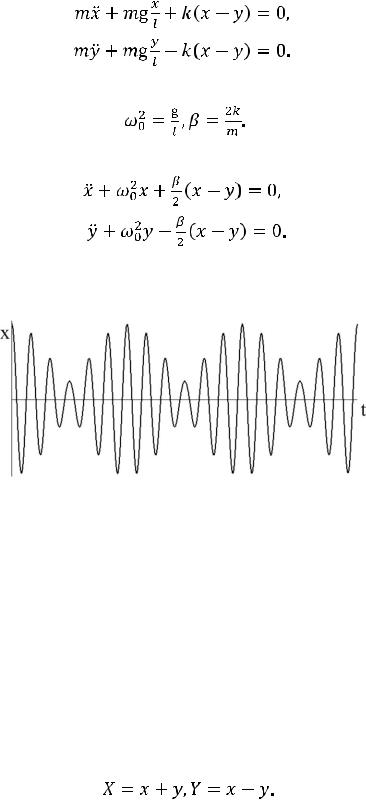
Будем рассматривать малые колебания в плоскости чертежа. Обозначим смещения точечных масс от их положения равновесия через х и y соответственно. Уравнения движения имеют вид
(14.1)
Введем обозначения
(14.2)
Перепишем уравнения (14.1) в виде
(14.3)
Решение системы двух уравнений (14.3) уже довольно сложно. График зависимости смещения х от времени, имеющий вид биений, приведен на рис. 14.2.
Рис. 14.2. График зависимости смешения одного из маятников от времени
Трудности решения быстро нарастают с ростом числа связанных элементов. Однако для любой физической системы, в которой действуют только возвращающие силы, можно ввести функции, удовлетворяющие независимым уравнениям колебательного движения.
Эти новые функции линейно связаны со смещениями отдельных элементов от положения равновесия, и их зависимость от времени является чисто гармонической.
НОРМАЛЬНЫЕ ПЕРЕМЕННЫЕ, НОРМАЛЬНЫЕ ЧАСТОТЫ. Проиллюстрируем
этот факт на примере двух связанных математических маятников. Введем две новые функции:
(14.4)
Функция Х с точностью до множителя 1/2 совпадает с координатой центра масс системы. Функция Y описывает относительное движение материальных точек в системе центра масс.
87
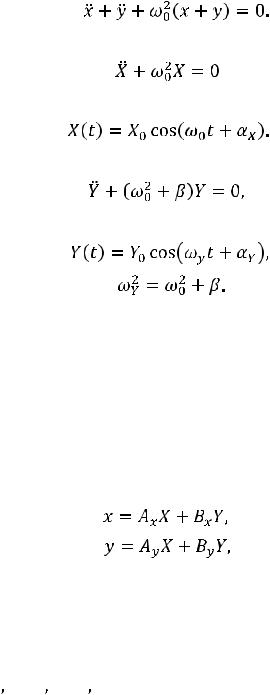
Складывая уравнения (14.3), получаем
(14.5)
С учетом (14.4) имеем уравнение
(14.6)
с гармоническим решением
(14.7)
Вычитая уравнения (14.3), получим уравнение
(14.8)
решением которого является гармоническая функция
(14.9)
где |
(14.10) |
Таким образом, движение системы упруго связанных осцилляторов описывается двумя функциями, каждая из которых удовлетворяет уравнению гармонических колебаний с разными частотами, определяемыми уравнениями (14.2) и (14.10). Переменные, позволяющие привести систему уравнений движения к набору уравнений независимых колебаний, называются нормальными переменными, соответствующие им частоты — нормальными частотами, а
решения отдельных уравнений — нормальными модами. Для двух одинаковых связанных осцилляторов нормальные переменные имеют вид (14.4).
Выражая смещения отдельных осцилляторов через нормальные моды
(14.11)
мы получим сложение гармонических колебаний одинакового направления и разных частот. Результатом такого сложения будут биения (рис. 14.2). Для однозначного определения зависимости смещений элементов системы от положения равновесия, кроме решений дифференциальных уравнений (14.3), необходимо знать также начальные условия: координаты и скорости в начальный момент времени 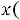
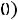
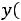
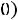
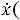
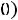
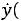
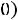 . Коэффициенты Ax, Bx, Ay, By, с которыми нормальные моды входят в решение исходной системы, определяются начальными условиями.
. Коэффициенты Ax, Bx, Ay, By, с которыми нормальные моды входят в решение исходной системы, определяются начальными условиями.
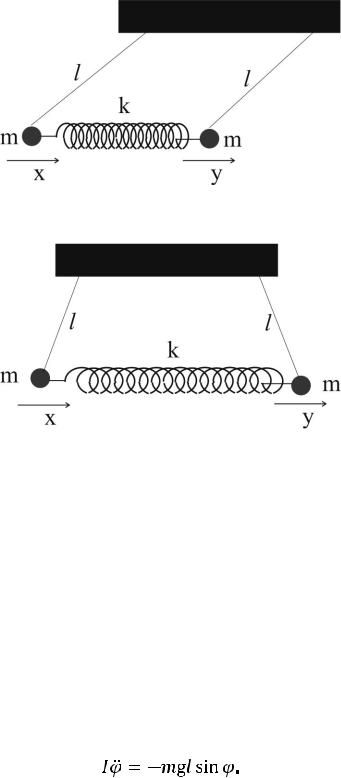
Существуют два предельных случая, когда нормальные моды можно наблюдать по отдельности. Если мы выведем оба осциллятора из положения равновесия на одинаковое расстояние и одновременно их отпустим, как показано на рис. 14.3, то они будут колебаться в одной фазе и пружина останется недеформированной.
Вследствие этого осцилляторы будут колебаться независимо, и во все моменты времени x = y и Bx = By = 0 (синфазная мода). Движение полностью описывается уравнением (14.6), частота колебаний обоих маятников совпадает
88
с частотой колебаний отдельного свободного маятника ω0, а жесткость связи не оказывает влияния на движение.
Рис. 14.3. Синхронные колебания двух одинаковых связанных маятников
Рис. 14.4. Колебания двух связанных маятников в противофазе
Если мы выведем оба осциллятора из положения равновесия, сместив на одинаковые по модулю, но противоположные по знаку расстояния, и одновременно их отпустим (рис. 14.4), то во все последующие моменты времени смещения x = -y и Ax = Ay = 0 (противофазная мода). Это движение полностью описывается уравнением (14.8). Частота таких колебаний больше частоты колебаний отдельного маятника.
НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ ФИЗИЧЕСКОГО МАЯТНИКА. Ранее мы изучили
колебания системы в малой окрестности положения устойчивого равновесия, которые всегда являются гармоническими. Теперь рассмотрим движение, возникающее при снятии ограничения на амплитуду колебаний. Вернемся к уравнению движения физического маятника (10.8)
(14.12)
Это дифференциальное уравнение уже не является линейным уравнением с постоянными коэффициентами и не может быть решено использованными ранее методами. Поскольку в системе действуют только консервативные силы, для поиска решения можно применить закон сохранения механической энергии
89

и понизить степень дифференциального уравнения. Кинетическая энергия вращающегося тела следующим образом связана с моментом инерции I и угловой скоростью 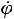 :
:
(14.13)
Потенциальную энергию будем считать равной нулю в нижнем положении маятника при θ = 0, то есть начало отсчета энергии понизим на величину l от точки подвеса О (рис. 14.5).
Тогда
(14.14)
и закон сохранения механической энергии имеет вид
|
|
|
|
(14.15) |
Рис. 14.5. Физический |
|
|
|
|
||
|
|
|
|
|
|
Вводя обозначения |
|
|
маятник |
||
|
|
на оси подвеса |
|||
|
|
|
|
|
|
(14.16)
выделим из уравнения (14.15)
(14.17)
Здесь частота ω0 совпадает с частотой малых гармонических колебаний рассматриваемого физического маятника. Режим движения маятника зависит от соотношения между полной энергией маятника E и его максимальной возможной потенциальной энергией Umax = 2mgl.
Если E < Umax, существует угол поворота θ0, при котором энергия полностью переходит в потенциальную, а кинетическая энергия, следовательно, и угловая скорость 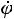 становятся равными нулю. В соответствии с уравнением (14.17) при равной нулю левой части должно выполняться равенство
становятся равными нулю. В соответствии с уравнением (14.17) при равной нулю левой части должно выполняться равенство
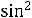
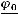
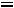
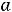 .
.
Таким образом, θ0 есть угловая амплитуда колебаний, которые совершает маятник при выполнении условия E < Umax.
Вслучае если E > Umax, справедливо неравенство a > 1 и в процессе движения маятник проходит наивысшую точку, продолжая вращательное движение в том же направлении.
Вслучае колебательного режима, извлекая квадратный корень из обеих частей равенства (14.17), получим
(14.18)
90
