3177

5.Выполняется ли принцип суперпозиции магнитных полей для ферромагнетиков?

6.Нарисуйте график зависимости относительной магнитной проницаемости μ(H) для диамагнетика и парамагнетика.

7.Нарисуйте график зависимости относительной магнитной проницаемости μ(H) для первоначально размагниченного ферромагнетика.

Глава 8. Электромагнитная индукция

При изучении силы Лоренца мы пришли к выводу, что деление поля на электрическую и магнитную компоненту имеет относительный характер и зависит от системы отсчета, в которой рассматривается задача. В частности, всегда может быть указана такая система, в которой отличной от нуля будет только одна из компонент электромагнитного поля. Вследствие этого электрическое и магнитное поля должны рассматриваться вместе как единый физический объ-

ект — электромагнитное поле.

ЭЛЕКТРОДВИЖУЩАЯ СИЛА ИНДУКЦИИ. Одним из законов, количественно описывающих связь между электрическим и магнитным полями, является закон индукции Фарадея, который записывается в виде

(8.1)

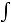
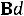
где ЭДС — электродвижущая сила индукции, то есть работа сторонних сил по перемещению единичного положительного заряда вдоль замкнутого проводящего контура, а 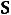— поток вектора магнитной индукции, пронизывающий площадь, охватываемую этим контуром.

СВЯЗЬ ЭДС С СИЛОЙ ЛОРЕНЦА. В общем случае закон индукции Фарадея (8.1) является фундаментальным законом природы и не сводится к другим уравнениям и законам. В частном случае его можно вывести, опираясь на выражение для силы Лоренца:

(8.2)

Рассмотрим замкнутый проводящий контур, показанный на рис. (8.1), в котором перемычка ab является подвижной.

Пусть магнитное поле В направлено перпендикулярно плоскости рисунка по направлению зрения. Это расположение показано на рисунке крестиком . При движении перемычки ab вправо в ней на каждый электрон будет действовать сила Лоренца (8.2) и возникнет сторонняя сила с напряженностью

(8.3)

51

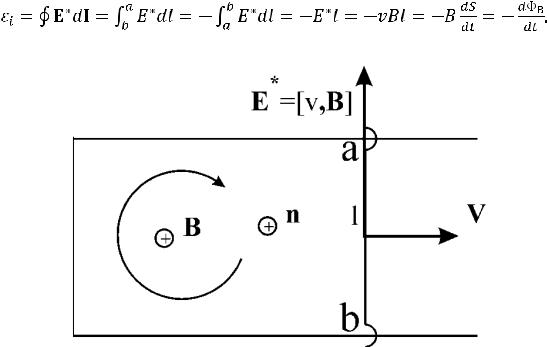
по правилу левой руки направленная от b к а. Легко вычислить циркуляцию вектора Е* по контуру, равную

(8.4)

Рис. 8.1. Действие силы Лоренца в проводящем контуре

Возникающий в контуре ток направлен вдоль направления E* и соответствует обходу контура против часовой стрелки. Вызываемое этим током магнитное поле направлено против внешнего поля. Тем самым увеличение магнитного потока через контур за счет увеличения его площади будет частично компенсироваться магнитным полем индукционного тока. Это правило применимо для определения направления индукционного тока (правило Ленца): индукционный ток в контуре направлен таким образом, чтобы скомпенсировать изменение внешнего магнитного потока. Данное правило выражается знаком (-) в формуле (8.1) и фактически показывает инерционность электромагнитного поля, поскольку индукционный ток направлен так, чтобы противодействовать причине, его вызывающей. Тем самым правило Ленца является частным случа-

ем общего принципа Ле-Шателье.

ВИХРЕВЫЕ ТОКИ. Индукционные токи могут возникать не только в замкнутых проводящих контурах, но и в сплошных массивных проводниках. Они носят вихревой характер (то есть линии тока замкнуты) и называются токами Фуко. Токи Фуко используются, например, в металлургической промышленности для плавления руды металлов. Токи Фуко обусловливают потери энергии в трансформаторах. Для уменьшения таких потерь трансформаторные сердечники делают разрезными, составленными из отдельных тонких листов стали. Высокочастотные индукционные токи протекают по поверхности проводников, не проникая вглубь. Поэтому это явление носит название скин-эффект (от англ. skin — «кожа»).

52

Электромагнитная индукция возникает во всех случаях изменения магнитного потока. Магнитный поток может меняться не только в результате перемещения контура, но также за счет изменения самого магнитного поля и при совокупном действии обеих причин.

ВЗАИМНАЯ ИНДУКЦИЯ. КОЭФФИЦИЕНТ ВЗАИМНОЙ ИНДУКЦИИ. Изменения

магнитного поля можно достичь путем изменения тока в проводящем контуре (проводнике). В расположенном вблизи этого контура втором проводнике (рис. 8.2) будет создаваться изменяющийся магнитный поток и возникнет ЭДС индукции. Магнитный поток во втором контуре

Ф2 пропорционален силе тока I1 в первом контуре:

(8.6)

Если коэффициент взаимной индукции не зависит от силы тока I1 в первом проводнике, то

(8.7)

При наличии ферромагнитных сердечников в системе или при возможности деформации контуров под действием магнитных сил L = L(I), и коэффициент взаимной индукции нельзя считать константой.

САМОИНДУКЦИЯ. КОЭФФИЦИЕНТ САМОИНДУКЦИИ. Еще одним важным

случаем электромагнитной индукции является возникновение ЭДС в самом контуре, где меняется ток. Пусть поток через контур, в котором протекает ток силой I, равен

(8.8)

где L называется коэффициентом самоиндукции. Он так же, как и коэффициент взаимной индукции, измеряется в генри (Гн). Индуктивностью 1 Гн обладает

53

контур, магнитный поток через который равен 1 Вб при токе в 1 А (Гн = Вб / А). При изменении тока в цепи в контуре возникает так называемая ЭДС самоиндукции:

(8.9)

Если L = const, то

(8.10)

Явление самоиндукции влияет на установление тока в цепи при ее замыкании и размыкании и позволяет описать так называемые переходные процессы.

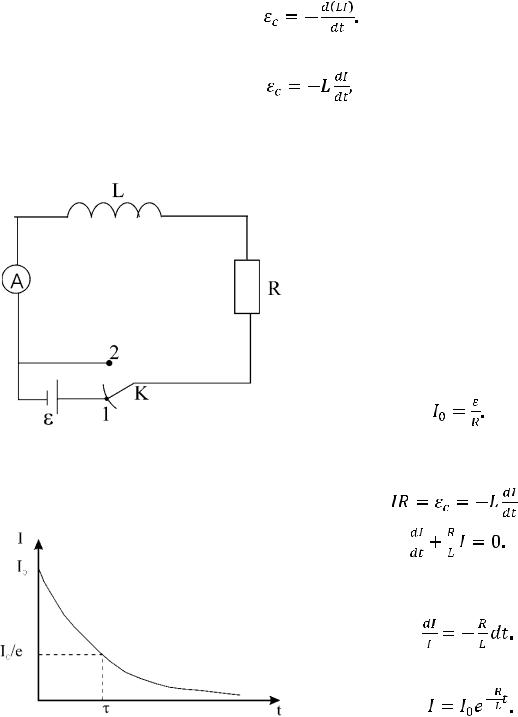
ТОК РАЗМЫКАНИЯ ЦЕПИ. Рассмот-

рим ток при размыкании цепи, показан-

ной на рис. 8.3. Размыкание соответствует перемещению ключа из положения 1 в положение 2.

В начальном положении 1, если оно выдерживается достаточно долго, протекает постоянный электрический ток. В соответствии с законом Ома для полной цепи с ЭДС ε его сила

(8.11)

После переключения цепи в положение 2 закон Ома примет вид

(8.12)

Разделяя переменные в уравнении (8.13), получаем:

(8.14)

Интегрирование (8.14) дает

(8.15)

Сила тока уменьшается с характерным временем η = L / R, как показано на рис. 8.4.

Формально ток существует в описанной нами модели бесконечно долго. В действительности через время t >> η он станет неразличим на фоне случайных тепловых колебаний концентрации электронов и его можно будет считать нулевым.

54

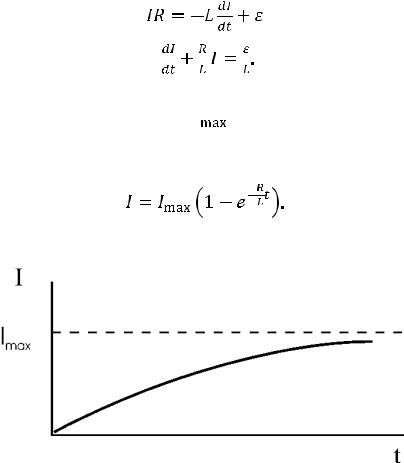
ТОК ЗАМЫКАНИЯ ЦЕПИ. Пусть теперь ток в цепи отсутствует, и мы замкнем цепь, переместив ключ из положения 2 в положение 1. После замыкания закон Ома примет вид

(8.16)

При замыкании цепи ток будет увеличиваться от нулевого значения, пока не достигнет максимальной величины, .

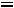
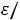
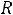Нетрудно убедиться, что этому условию и уравнению (8.7) удовлетворяет решение

(8.18)

График зависимости тока замыкания от времени показан на рис. 8.5.

Рис. 8.5. Закон изменения силы тока при замыкании цепи

Характерное время η = L / R, за которое ток в цепи достигает макси-

мального значения, называется временем переходного процесса (временем релаксации).

К о н т р о л ь н ы е в о п р о с ы и у п р а ж н е н и я

1.Перечислите условия, при которых возникает явление электромагнитной индукции.

2.Что означает знак минус в законе индукции Фарадея?

3.В чем отличие явления самоиндукции от явления взаимной индукции проводников?

4.За счет чего можно изменить магнитный поток через замкнутый контур?

5.Дайте качественное объяснение явлению постепенного нарастания силы тока при замыкании цепи с источником постоянного тока.

6.Почему при отключении утюга из розетки проскакивает искра?

55

Глава 9. Уравнения Максвелла

Изученные нами законы электродинамики можно свести теперь к четырем уравнениям в интегральной форме:

(9.1)

(9.2) (9.3)

(9.4)

ФИЗИЧЕСКИЙ СМЫСЛ УРАВНЕНИЙ МАКСВЕЛЛА В ИНТЕГРАЛЬНОЙ ФОРМЕ.

Первое уравнение (9.1) показывает, что источниками электрического поля являются электрические заряды. Второе уравнение (9.2) демонстрирует замкнутость линий индукции магнитного поля и отсутствие источников (зарядов) магнитного поля. Третье уравнение (9.3) представляет собой теорему о полной циркуляции вектора напряженности магнитного поля, в которой полный ток выражен через вектор плотности тока. Уравнение (9.4) является записью закона электромагнитной индукции Фарадея.

ТОК СМЕЩЕНИЯ. Максвелл обратил внимание на то, что в уравнениях, справедливых для постоянных токов, отсутствует симметрия между электрическим и магнитным полями. Действительно, в соответствии с уравнением (9.4) переменное магнитное поле создает вихревое электрическое поле и следует ожидать, что и переменное электрическое поле должно порождать магнитное поле. В то же время уравнение (9.3) показывает, что вихревое магнитное поле создается только за счет тока электрических зарядов.

Для того чтобы устранить такую несимметричность теории, рассмотрим протекание переменного тока в цепи с конденсатором, как показано на рис. 9.1. Если вычислить циркуляцию магнитного поля по контуру, охватывающему поверхность S1, то в соответствии с уравнением (9.3) получится некоторое ненулевое значение.

Рис. 9.1. Расположение поверхностей при определении величины тока смещения в конденсаторе

56

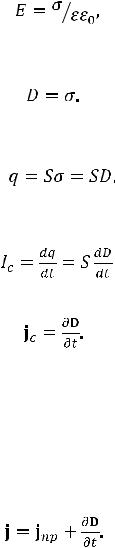
Если теперь деформировать поверхность таким образом, что она замкнется через пространственный промежуток между пластинами конденсатора, то поток вектора плотности тока проводимости j теперь будет равен нулю, в то время как контур не изменился и циркуляция магнитного поля осталась ненулевой. Это приводит к нарушению справедливости уравнения (9.3). Следовательно, для того чтобы уравнение сохранило свою справедливость и в этом случае, электрическое поле в конденсаторе должно создавать такое же магнитное поле, как если бы между обкладками существовал ток, имеющий такую же силу, как и в подходящих к конденсатору проводниках. Это условие позволяет найти связь между переменным электрическим полем внутри конденсатора и создаваемым им магнитным полем. В соответствии с уравнением для напряженности электрического поля внутри конденсатора

(9.5)

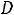
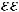
модуль вектора электрической индукции 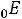равен поверхностной плотности заряда на положительной обкладке конденсатора:

(9.6)

Следовательно, заряд обкладки пропорционален ее площади и величине вектора электрической индукции:

(9.7)

Если за время dt заряд конденсатора меняется на dq, в проводах течет ток, называемый током смещения силой

(9.8)

и плотностью

(9.9)

Знак частной производной в уравнении (9.9) отражает тот факт, что для неоднородного электрического поля D (r, t) магнитное поле возникает только за счет изменения вектора электрической индукции D во времени. Если в проводнике течет переменный ток, то в нем одновременно существуют и направленное движение зарядов, называющееся током проводимости, и переменное электрическое поле. Поэтому плотность полного j тока складывается из плотностей токов проводимости jпр и смещения jс:

(9.10)

При таком определении полного тока его линии являются замкнутыми, вследствие чего поток вектора полного тока теперь не меняется при деформациях поверхности. В частности, поток оказывается одинаковым для поверхностей S1 и S2 на рис. 9.1. Наличие тока смещения, плотность которого пропорциональна скорости изменения электрического смещения, восстанавливает симметрию электрического и магнитного полей. Теперь не только переменное

57

магнитное поле в соответствии с (9.4) порождает электрическое, но и переменное электрическое поле порождает магнитное. Заменяя в уравнении (9.3) ток проводимости на полный ток (9.10), окончательно получим уравнение Максвелла

(9.11)

Здесь и далее под j будет пониматься плотность тока проводимости, а индекс «пр» будет опущен. Уравнение (9.11) предусматривает возможность возбуждения вихревого магнитного поля за счет переменного электрического поля.

СКОРОСТЬ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ. Взаимосвязь электрического и

магнитного полей объясняет появление и распространение электромагнитных волн. Рассмотрим плоскую электромагнитную волну и определим скорость ее распространения. Плоская электромагнитная волна характеризуется тем, что она во всех точках пространства имеет одинаковое направление распространения. Рис. 9.2 изображает часть плоской волны. Передняя часть волны (крайняя правая на рис. 9.2) называется фронтом волны. Фронт волны лежит в плоскости, перпендикулярной к направлению ее распространения (перпендикулярно к плоскости рисунка). За фронтом волны (на рис. 9.2 слева) имеется однородное электрическое поле с напряженностью Е, перпендикулярной плоскости чертежа, направленное от нас (оно изображено в сечении крестиками), и однородное магнитное поле с напряженностью Н, направленной вверх в плоскости чертежа.

Такая волна может возникнуть, например, при быстрой зарядке полубесконечной плоскости. Спереди от фронта волны (на чертеже справа) нет ни электрического, ни магнитного поля. Фронт волны движется направо со скоростью V. Выберем квадратный контур в плоскости чертежа, как показано на рис. 9.2.

Тогда до достижения фронтом волны правой стороны контура интеграл теоремы о полной циркуляции по периметру квадрата равен просто HL. Чтобы пересечь квадрат шириной L, волне требуется время t, определяемое соотноше-

58

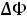
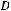
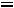
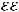
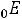
нием t = L / V, где V — скорость распространения волны. Полное изменение потока вектора электрической индукции за это время равно 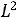. Скорость изменения потока равна

.

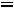
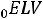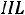
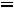
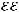
В соответствии с уравнением Максвелла (9.11) 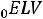, то есть

(9.12)

Аналогичным образом, выбирая квадратный контур в плоскости, перпендикулярной плоскости чертежа, получим из уравнения Максвелла (9.4)

(9.13)

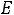
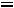
то есть 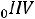. Подставляя (9.13) в (9.12), получим выражение для скорости распространения электромагнитной волны в виде

(9.14)

Мы рассмотрели уравнения Максвелла в интегральной форме. Часто, когда задача не обладает симметрией, более перспективным оказывается путь, основанный на дифференциальной форме уравнений Максвелла. Дифференциальной называется такая форма уравнений, в которой все входящие в них величины заданы в одной точке.

Исходя из этого определения ясно, что для получения дифференциальной формы необходимо сделать бесконечно малыми области интегрирования в уравнениях (9.1), (9.2), (9.4) и (9.11).

ПОТОК ВЕКТОРА ЧЕРЕЗ БЕСКОНЕЧНО МАЛУЮ ПОВЕРХНОСТЬ. Рассмотрим

вначале, как выглядит при стягивании в точку поверхности выражение для потока вектора.

Вычислим поток произвольного вектора (например, D) через поверхность бесконечно малого куба, три грани которого совпадают с координатными плоскостями, а длины ребер равны dx, dy, dz (рис. 9.3).

Рис. 9.3. Форма поверхности для вычисления локального потока

59

Рассмотрим поток через грани, перпендикулярные оси х. Поскольку нормаль к правой грани направлена в положительном, а к левой — в отрицательном направлении оси х, поток d x есть разность модулей потоков через эти грани:

(9.15)

Аналогично для граней, перпендикулярных к осям у и z, имеем

(9.16)

Суммируя (9.15) и (9.16), получим поток через всю поверхность:

(9.17)

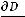
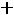
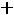
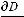
В теории поля выражение называется дивергенцией вектора D и обозначается divD. Используя это обозначение, имеем

(9.18)

где dV — элемент объема. Следовательно, интегрирование по поверхности в левой части уравнения (9.1) можно заменить интегрированием по заключенному в ней объему:

(9.19)

Уравнение (9.1) можно переписать в дифференциальной форме:

(9.20)

Аналогично из уравнения (9.2) получим

(9.21)

60