3177

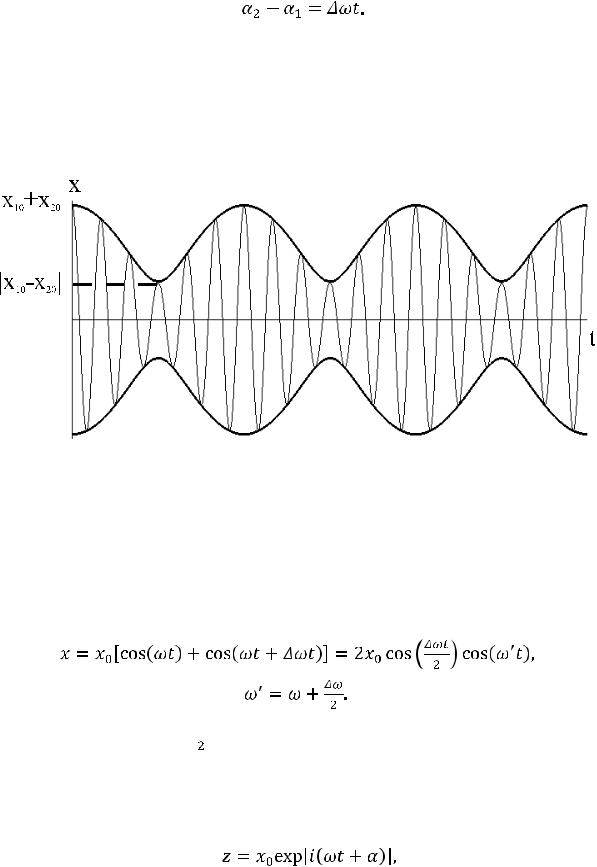
быть жестким и результирующее колебание не является гармоническим. Его амплитуда по-прежнему может быть представлена в виде (11.3), однако разность фаз складываемых колебаний теперь пропорциональна времени:

(11.5)

Если частоты складываемых колебаний близки, то есть ω << ω, то амплитуда результирующего колебания медленно меняется во времени. При этом результирующее колебание близко к гармоническому. Такие колебания носят название биения. Характерная картина биений приведена на рис. 11.2. Тонкой кривой изображено смещение, а жирной — медленно меняющаяся во времени амплитуда огибающей.

Рис. 11.2. Образование биений в результате сложения колебаний с близкими частотами

Всоответствии с уравнением (11.3) амплитуда биения изменяется с час-

тотой ω/2 от величины x0 = x20 - x10 (в те моменты, когда векторные амплитуды направлены противоположно) до значения x0 = x20 + x10 (в те моменты, когда векторные амплитуды имеют одинаковое направление). В случае одинаковых амплитуд эти результаты могут быть легко получены аналитически.

Врезультате сложения колебаний получим

(11.6)

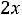
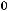
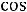
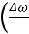
Множитель 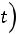играет роль медленно меняющейся амплитуды.

КОМПЛЕКСНОЕ ПРЕДСТАВЛЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ. Кроме дей-

ствительного решения в виде гармонических функций дифференциальное уравнения гармонических колебаний (10.5) имеет комплексное решение:

(11.7)

71

(11.9)

уравнение (11.7) можно представить в виде

(11.10)

где

(11.11) (11.12)

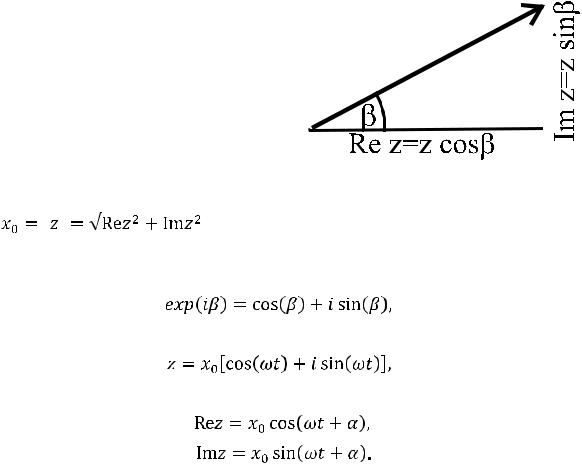
Физическим смыслом обладает действительная часть решения (11.11), совпадающая с решением в форме (10.6).

Для одного гармонического колебания предпочтительно сразу выбирать решение в виде (10.6), минуя вспомогательное уравнение (11.7) и последующий переход (11.10). Однако, поскольку операции дифференцирования и интегрирования с экспоненциальной функцией (11.7) проще, чем с косинусом, в более сложных случаях при решении уравнений колебаний использование комплексного решения (11.7) оказывается очень полезным.

Комплексное представление гармонических колебаний позволяет с новой точки зрения взглянуть на метод векторных диаграмм. В комплексном представлении векторная амплитуда x1 есть просто графическое изображение комплексного числа x01exp (iα) на комплексной плоскости. Вращение векторной диаграммы с угловой скоростью ω соответствует умножению амплитуды на exp (iωt), а проектирование на действительную ось — операции вычисления действительной части. Таким образом, геометрическое сложение векторных амплитуд можно заменить алгебраическим сложением комплексных амплитуд x01exp (iα).

Особенно эффективным является этот прием в двух случаях:

1) при сложении большого числа колебаний одинаковой амплитуды и кратных начальных фаз. В этом случае слагаемые представляют собой члены геометрической прогрессии. Этот метод будет применен в дальнейшем при сложении когерентных волн;

72

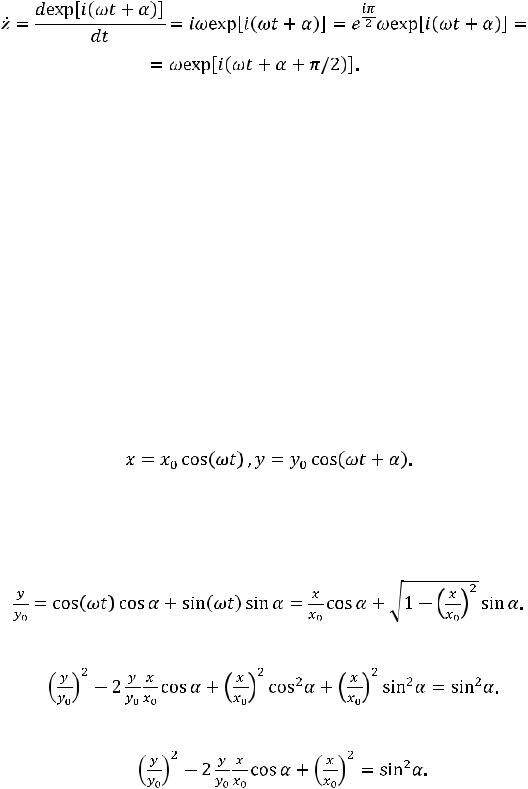
2) при сложении колебаний, получающихся в результате дифференцирования или интегрирования исходного гармонического колебания. В этом случае начальные фазы получаемых колебаний отличаются от исходной на величину кратную π/2. Покажем, что такое изменению фазы происходит, например, при дифференцировании функции вида (11.7):

(11.13)

Можно сформулировать следующие правила обращения с колебаниями, представленными в комплексной форме:

1)умножение комплексной амплитуды на мнимую единицу приводит к повороту вектора амплитуды на угол π/2 против часовой стрелки;

2)дифференцирование уравнения гармонических колебаний приводит к увеличению их фазы на π/2 и умножению амплитуды на частоту ω;

3)интегрирование уравнения гармонических колебаний приводит к уменьшению их фазы на π/2 и делению амплитуды на частоту ω.

Проверку последнего правила полезно проделать самостоятельно. Эти правила будут неоднократно применяться в дальнейшем.

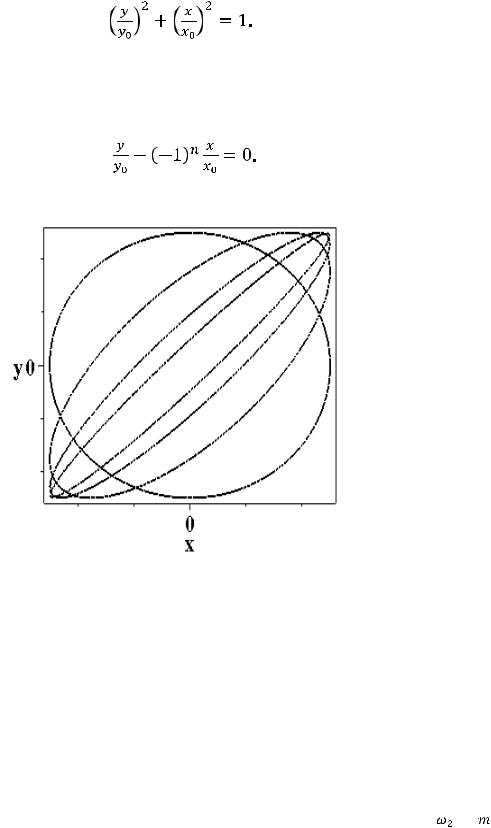
СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ ОДИНАКОВОЙ

ЧАСТОТЫ. Пусть частица участвует одновременно в двух взаимно перпендикулярных колебаниях. Совместив оси Х и Y системы координат с направлениями колебаний и выбрав начальный момент времени так, чтобы начальная фаза колебания по оси Х равнялась нулю, запишем смещение по осям в виде

(11.14)

Эта система уравнений задает траекторию частицы в параметрической форме. Для определения траектории в явной форме исключим из (11.14) параметр t. Разделив обе части второго из уравнений системы на y0, раскрыв косинус суммы и учтя, что в соответствии с первым уравнением cos(ωt) = x / x0, получим

(11.15)

Уединяя радикал и возводя обе части равенства в квадрат, имеем

(11.16)

Окончательно получим уравнение траектории в виде

(11.17)

Уравнение (11.17) представляет собой общее уравнение эллипса.

73

Вданном случае оси эллипса не совпадают с осями координат, но при

α= π/2 уравнение (11.17) упрощается:

(11.18)

В этом виде оно описывает эллипс с полуосями длиной y0, x0, совпадающими по направлению с координатными осями Х и Y.

При α = nπ (здесь n = 0, 1, 2,…) уравнение (11.17) вырождается в уравнение отрезка прямой:

(11.19)

Траектории для α = π/2, π/4, π/8, π/16 и y0 = x0 изображены на рис. 11.3.

Рис. 11.3. Траектории в форме эллипса при сложении взаимно перпендикулярных колебаний одинаковой частоты

СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ С РАЗНЫМИ ЧАСТО-

ТАМИ. ФИГУРЫ ЛИССАЖУ. Эллипс представляет собой частный случай траектории частицы, участвующей во взаимно перпендикулярных колебаниях. В общем случае такие траектории называются фигурами Лиссажу.

Хотя уравнения этих кривых достаточно сложны, их некоторые общие свойства могут быть сформулированы.

1. Вид траектории зависит только от отношения частот складываемых колебаний. Если это отношение является рациональным числом, то есть ,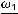

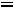
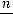где n, m — целые числа, траектория периодически повторяется.

2. Фигура Лиссажу всегда ограничена прямоугольником со сторонами 2y0, 2x0. Траектории всегда касаются сторон этого прямоугольника.

74

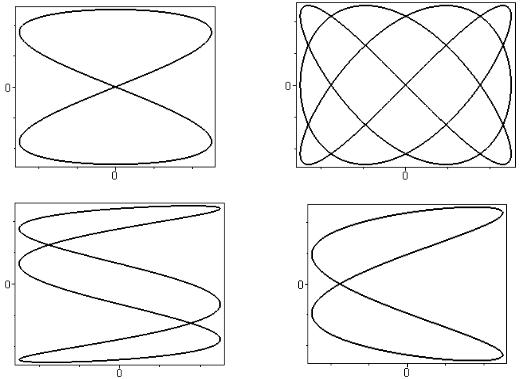
3. При рациональном отношении частот отношение числа точек касания, лежащих на оси Х, к числу точек касания, лежащих на оси Y, обратно пропорционально отношению соответствующих частот.

Примеры кривых Лиссажу приведены на рис. 11.4. Полезно самостоятельно проанализировать, какому соотношению частот соответствуют разные фигуры рисунка.

Рис. 11.4. Фигуры Лиссажу

К о н т р о л ь н ы е в о п р о с ы и у п р а ж н е н и я

1. Какова максимальная и минимальная амплитуда результирующего колебания, возникающего при сложении колебаний одинакового направления с амплитудами x01 и x02?

2.При какой разности начальных фаз складываемых колебаний одинакового направления амплитуда результирующего колебания максимальна? Минимальна?

3.Определить амплитуду и фазу результирующего колебания, возникающего при сложении колебаний одинакового направления, описываемых уравнениями: x1 = 2cos(2t + π/2), x1 = 4cos(2t + π/4). Нарисовать векторную диаграмму.

4.Определить траекторию частицы, участвующей во взаимно перпенди-

кулярных колебаниях x = 2cos(2t + π/2), y = 4cos(2t + 3π/2).

5.Начальная фаза гармонического колебания равна π/2, а частота равна

πс-1. Определить зависимость фазы скорости и ускорения от времени.

75

Глава 12. Затухающие колебания

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ЗАТУХАЮЩИХ МЕХАНИЧЕСКИХ КОЛЕ-

БАНИЙ И ЕГО РЕШЕНИЕ. До сих пор мы рассматривали идеализированные гармонические колебания, в которых механическая энергия сохранялась и смещение изменялось по закону косинуса неограниченно долго. В действительности в любой реальной системе на каждом такте колебаний некоторая доля механической энергии переходит в тепло из-за наличия сил трения. Этот процесс называется диссипацией энергии. Поэтому в отсутствие внешних поддерживающих колебание воздействий амплитуда осциллятора всегда будет уменьшаться во времени.

В случае вязкого трения при малых скоростях движения наличие сопротивления описывается с помощью силы , пропорциональной скорости и направленной противоположно ей. Второй закон Ньютона для системы, в которой действует возвращающая сила (10.2), с учетом диссипации имеет вид

(12.1)

Часто уравнение (12.1) применяют и при наличии других видов трения. В этом случае оно уже не описывает колебания количественно правильно, хотя качественно многие характеристики остаются близкими к более простому случаю, который мы рассматриваем. Перенося все слагаемые в левую часть, деля равенство на массу частицы m и вводя обозначения

(12.2)

приведем уравнение (12.1) к виду

(12.3)

Решим это уравнение методом комплексной амплитуды. Для этого подставим вместо x функцию

(12.4)

в дифференциальное уравнение (12.3) и получим характеристическое алгебраическое уравнение

(12.5)

Корни квадратного уравнения (12.5) имеют вид

(12.6)

Вид решения уравнения (12.5) зависит от соотношения между параметрами δ и ω0. При δ > ω0 сила трения очень велика и оба корня уравнения (12.6) действительны и отрицательны. В этом случае система плавно возвращается в состояние равновесия с нулевым смещением без осцилляций около положения равновесия. Процесс в этом случае не является колебательным и носит назва-

76

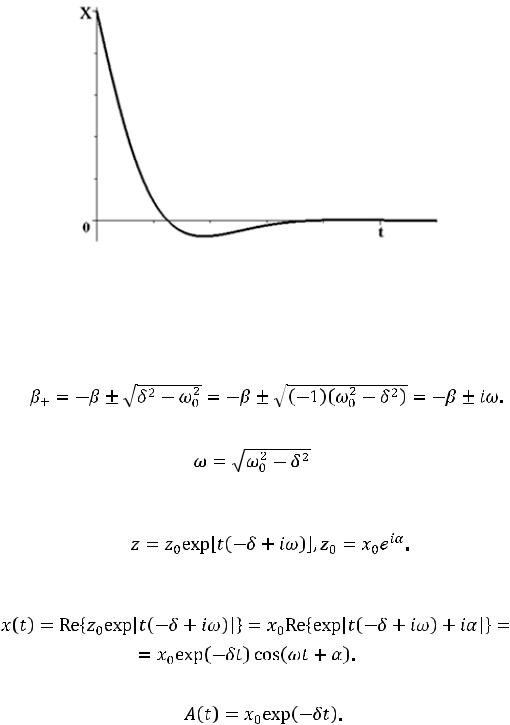
ние апериодического. Для иллюстрации на рис. 12.1 приведена зависимость смещения от времени в системе с большой силой трения. Мы не будем исследовать его более подробно.

Рис. 12.1. Затухающее апериодическое колебание

При δ < ω0 движение хотя и не является строго периодическим, но характеризуется повторяемостью во времени. Решение (12.6) может быть преобразовано следующим образом:

(12.7)

Здесь введено обозначение

(12.8)

для величины, играющей роль частоты затухающих колебаний. Одно из комплексных решений уравнения (12.3) имеет вид

(12.9)

Вычисляя действительную часть решения (12.9), получаем решение исходного уравнения затухающих колебаний (12.3):

(12.10)

Роль амплитуды в решении (12.10) играет затухающий множитель

(12.11)

Хотя формально в решении время с начала до полного прекращения затухающих колебаний бесконечно, практически при достаточно больших временах отличием амплитуды от нуля на фоне флуктуаций можно пренебречь. В физике принято характеризовать скорость экспоненциального затухания временем η, необходимым для уменьшения амплитуды в e раз. Это время называется по-

стоянной времени затухания, или временем релаксации.

77

В соответствии с уравнением (12.11)

(12.12)

Подставляя (12.12) в (12.11), получим

(12.13)

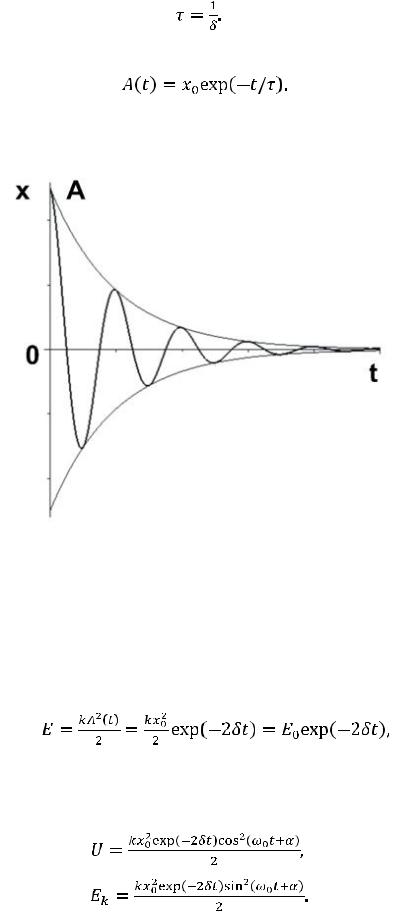
График зависимости смещения (жирная линия) и амплитуды (тонкая линия) затухающих колебаний от времени приведен на рис. 12.2.

Рис. 12.2. Затухающие колебания

ЭНЕРГИЯ ЗАТУХАЮЩЕГО ОСЦИЛЛЯТОРА. В соответствии с уравнением

(10.26) полная механическая энергия осциллятора в точке максимального смещения от положения равновесия пропорциональна квадрату амплитуды колебаний. Вследствие диссипации механическая энергия затухающих колебаний уменьшается по экспоненциальному закону:

(12.14)

где E0 — механическая энергия при t = 0. Зависимости потенциальной энергии U и кинетической энергии Ek от времени при малом затухании описываются уравнениями, аналогичными (10.24) и (10.25):

(12.15)

(12.16)

78

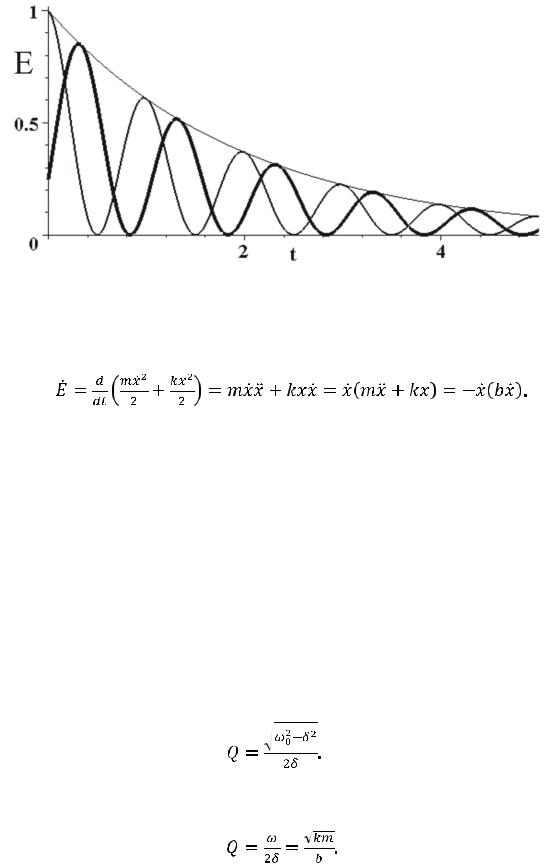
График зависимости потенциальной (жирная сплошная линия), кинетической (тонкая сплошная линия) и полной энергии (монотонная кривая) затухающих колебаний от времени приведен на рис. 12.3.

Рис. 12.3. Зависимость потенциальной и кинетической энергии затухающих колебаний от времени

Рассчитаем скорость уменьшения механической энергии осциллятора :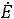

(12.17)

Здесь учтено, что в соответствии с законом движения (12.1)

.

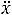
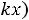
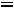
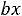
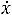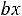
Поскольку есть пройденный в единицу времени путь, а — сила трения, то уравнение (12.17) имеет простой физический смысл: скорость уменьшения механической энергии равна работе силы трения в единицу времени, то есть мощности этой силы.

ДОБРОТНОСТЬ ОСЦИЛЛЯТОРА С ЗАТУХАНИЕМ. Безразмерная величина —

добротность Q характеризует скорость диссипации энергии. Она определяется как изменение фазы колебаний при уменьшении полной энергии в e раз. Как следует из уравнения (12.14), время этого процесса равно 1/2δ. Умножая это время на частоту ω из уравнения (12.8), мы получим изменение фазы за это время или добротность:

(12.18)

При малом затухании δ << ω0 и, следовательно, при большой добротности уравнение (12.18) можно упростить, так что

(12.19)

79

Здесь использованы соотношения (12.2).

При δ << ω механическая энергия, теряемая за один период T, может быть определена следующим образом:

(12.20)

Таким образом, добротность характеризует отношение полной энергии системы E к энергии ΔE, теряемой за один период:

(12.21)

Добротность является важной характеристикой осциллятора с затуханием.

ЗАТУХАЮЩИЕ КОЛЕБАНИЯ В ЭЛЕКТРИЧЕСКОМ КОНТУРЕ. Так же, как в ме-

ханической системе, наличие силы трения приводит к диссипации энергии, наличие сопротивления электрической цепи R приводит к переходу электрической энергии в тепло. Закон Ома для замкнутой цепи (рис. 12.4), состоящей из катуш-

ки индуктивности L, конденсатора C и со-

противления R, с учетом самоиндукции в катушке имеет вид

(12.22)

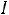
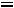
Учитывая, что 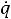, получаем

(12.23)

Уравнение (12.23) совпадает с уравнением (12.1) при заменах параметров

(12.25)

Добротность электрического контура определяется его сопротивлением, емкостью и индуктивностью, и при малом затухании

(12.27)

Параметр δ имеет размерность частоты c-1, а произведение ωL имеет размерность сопротивления R Ом. В Омах измеряется также величина .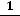

80