3177

Циркуляция dCz по прямоугольнику есть сумма интегралов по его сторонам. Учитывая, что направление обхода двух сторон совпадает с положительным, а двух — с отрицательным направлением осей координат, имеем

(9.22)

Разложим проекции напряженности Е с точностью до первых степеней приращений аргументов dx, dy:

(9.23)

Здесь dSz есть величина перпендикулярной оси z площадки. Для площадок, перпендикулярных осям х и у, аналогично можно получить

(9.24)

Вектор с компонентами в скобках выражений (9.22) и (9.23) называется ротором Е и обозначается rot E:

(9.25)

Уравнения (9.4) и (9.11) справедливы и для произвольно ориентированных площадок, а не только для тех, чьи плоскости совпадают с координатными плоскостями.

Поэтому закон электромагнитной индукции (9.4) может быть записан в следующей форме:

(9.26)

УРАВНЕНИЯ МАКСВЕЛЛА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ. Меняя порядок

дифференцирования и интегрирования в правой части уравнения (9.26), получим закон электромагнитной индукции в дифференциальной форме:

(9.27)

Проделав те же операции и для уравнения (9.11), получим закона полного тока в дифференциальной форме:

(9.28)

Совокупность уравнений (9.20), (9.21), (9.27) и (9.28) образует систему уравнений Максвелла в дифференциальной форме. Физическое содержание уравнений как в дифференциальной, так и в интегральной форме одинаково. Вопрос, какой из форм пользоваться, решается исходя из особенностей конкретной задачи.

61

К о н т р о л ь н ы е в о п р о с ы и у п р а ж н е н и я

1.Какие законы выражает каждое из уравнений Максвелла?

2.В чем заключается смысл введения тока смещения?

3.Как из интегральных соотношений получить операцию div?

4.Как из интегральных соотношений получить операцию rot?

5.Чему равна скорость света в веществе с μ = 1, 2, ε = 1,5?

Р а з д е л I I К о л е б а н и я

Глава 10. Гармонические колебания

КОЛЕБАНИЯ. Многие системы в природе и технике имеют одно или несколько состояний устойчивого равновесия. Если система выведена из равновесия внешним воздействием, то происходит самопроизвольное возвращение системы в состояние равновесия под действием внутренних сил. Обычно существует граница внешних воздействий, без выхода за которую система всегда возвращается в состояние равновесия.

Поведение большого числа систем вблизи положения устойчивого равновесия подчиняется общим законам и может быть описано одинаковыми уравнениями. Происходящие при этом процессы характеризуются повторяемостью во времени и носят название колебаний. Мы рассматриваем поведение физических систем, однако для демонстрации общего характера колебательных закономерностей приведем два нефизических примера колебаний. Колебательный характер имеет процесс изменения численности популяции животных при периодическом изменении внешних условий или в экологической системе, состоящей из совокупности хищников и их жертв, например рысей и зайцев. Колеблется около равновесия и цена товара при изменении спроса и предложения.

Проще всего математически описывается поведение системы, состояние которой определяется одним параметром x — отклонением от положения равновесия. Такие системы называются одномерными. Движение системы к положению равновесия обусловлено тем, что в ответ на внешнее возмущение x в системе возникает отклик:

(10.1)

где k(x) — положительная функция, а знак (–) означает, что отклик системы направлен противоположно внешнему воздействию. Такой отклик называется возвращающей силой. Следует понимать определенную условность этого термина. Смысл величины F зависит от характера исследуемого явления, и она не всегда является силой даже для механических процессов. Отклик (10.1) стремится вернуть систему к положению равновесия только при условии k(x) > 0. Это условие

62

и определяет верхнюю границу воздействия k(x) = 0, после перехода через которую k(x) < 0 и система уже не стремится вернуться в исходное состояние.

Приведем примеры физических колебательных систем и выясним смысл возвращающей силы в конкретных случаях. Рассмотрим вначале системы, в которых k(x) есть постоянная величина, и покажем, что поведение таких систем описывается простейшими периодическими функциями времени — cos и sin. Такие колебания называются гармоническими, а системы, их совершающие, — линей-

ными, или гармоническими осцилляторами (в дальнейшем — осцилляторами).

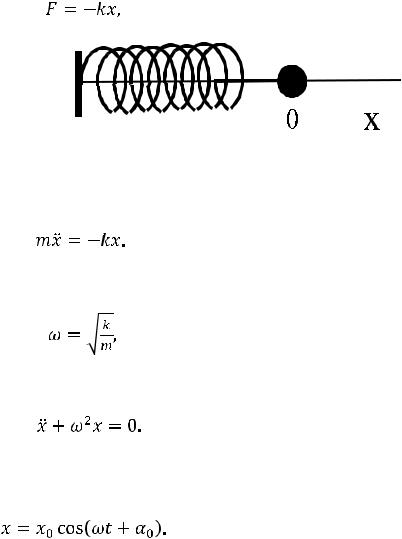
ПРУЖИННЫЙ МАЯТНИК. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ГАРМОНИЧЕС- КИХ КОЛЕБАНИЙ И ЕГО РЕШЕНИЕ. Рассмотрим поведение пружинного маятника,

то есть тела массой m, движущегося без трения по горизонтальной оси х под действием упругой силы, подчиняющейся линейному закону Гука:

Перенося член -kx в левую часть равенства, деля его на m и вводя обозна-

чение

(10.4)

получаем линейное дифференциальное уравнение второго порядка с постоянными коэффициентами:

(10.5)

Уравнение (10.5) есть дифференциальное уравнение гармонических коле-

баний. Легко проверить (полезно проделать это самостоятельно), что общее решение уравнения (10.5) имеет вид

(10.6)

Максимальное смещение от положения равновесия x0 называется амплитудой, аргумент гармонической функции α = (ωt + α0) — фазой, величина α0 —

начальной фазой колебаний, а ω — круговой (циклической) частотой. Выбор начальной фазы α0 означает определенный выбор начала отсчета времени, и ее всегда можно сделать для одного независимого гармонического колебания рав-

63

ной нулю за счет изменения начала такого отсчета. Поэтому всюду в дальнейшем, где это не существенно, мы будем полагать α0 = 0. Наряду с ω применяет-

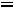
ся связанная с ней простым соотношением величина , называемая час-

тотой (иногда линейной частотой). Поскольку в дальнейшем мы редко будем использовать линейную частоту, прилагательное «круговая» будет опускаться. Частота измеряется в рад/с, но поскольку радианная мера углов является стандартной, то соответствующее указание обычно опускается и пишут 1/с.

Величина ω имеет простой физический смысл. Поскольку период гармонической функции равен 2π, то, если к времени t в уравнении (10.6) добавить слагаемое

(10.7)

значение гармонической функции не изменится. Таким образом, T в (10.7) есть период колебаний.

Свойства системы определяют только частоту ω и, следовательно, период T. Константы x0 и α, возникающие в решении дифференциального уравнения, определяются первоначальным внешним воздействием. При этом амплитуда x0 зависит от его величины, а начальная фаза α определяется моментом времени, от которого ведется отсчет колебаний.

где θ — угол поворота, I — момент инерции маятника относительно оси О, а момент силы тяжести M является в этом случае возвращающей силой и следующим образом выражается через расстояние l от оси вращения до центра масс С и вес тела mg:

(10.9)

Здесь lsin(θ) = h есть плечо силы (рис. 10.2). При малых колебаниях можно считать, что

(10.10)

64

Тогда уравнение (10.8) приобретает вид

(10.11)

Перенося слагаемое 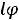в левую часть равенства и деля получающееся равенство на I, имеем уравнение

(10.12)

совпадающее с уравнением (10.5) при заменах x → θ и

(10.13)

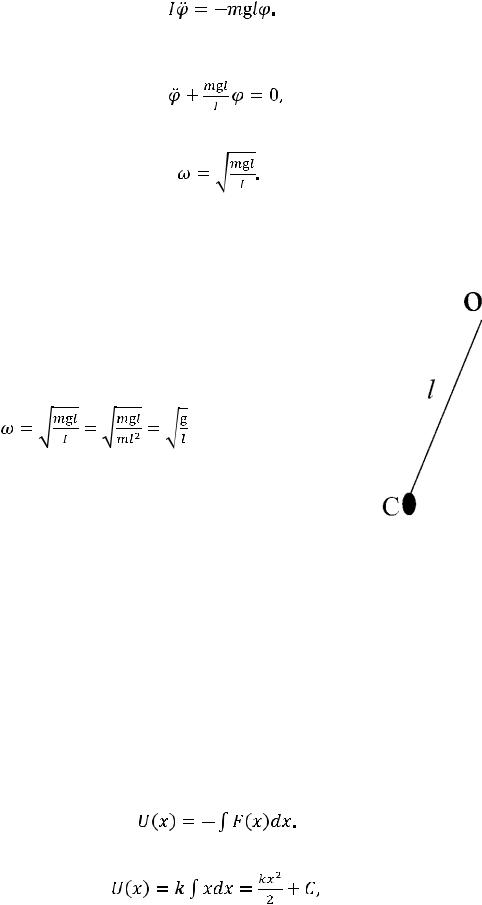
Если физический маятник с достаточной для решения конкретной задачи точностью можно описывать моделью материальной точки, то момент инерции имеет вид I = ml2. Такая колебательная система называется математическим маятником.

Моделью математического маятника достаточно хорошо описывается твердое тело, подвешенное на нити, длина которой много больше размеров тела, а масса много меньше массы тела (рис. 10.3). Частота колебаний математического маятника

(10.14)

и зависит только от его длины и ускорения свободного падения.

МАЛЫЕ КОЛЕБАНИЯ В ОКРЕСТНОСТИ ПОЛОЖЕ- НИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ. Физический маят-

ник является примером системы, которую можно лишь приближенно считать линейной. Понятие линейности играет большую

роль в физике и математике и подробно разбирается в курсе линейной алгебры. Для колебательных систем наиболее важным проявлением линейности является то, что если в системе возможны два вида колебаний, то возможно и колебание, являющееся их суммой.

Точность линейного приближения при описании физического маятника определяется выполнением условия (10.10). Выясним, каким требованиям должна удовлетворять система в общем случае, для того чтобы в ней могли происходить гармонические колебания. Как известно из механики, потенциальная энергия U следующим образом связана с силой:

(10.15)

Для упругой силы, подчиняющейся закону Гука (10.2), имеем

(10.16)

65

где C — произвольная постоянная. С другой стороны, разлагая произвольную потенциальную энергию U (x) в ряд Тейлора в окрестности положения равновесия x = 0, получим

(10.17)

Уравнение (10.17) совпадает с (10.16) при выполнении трех условий:

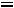
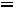
1. Производная 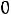, и, следовательно, в точке x = 0 функция

имеет экстремум. В отсутствие внешних воздействий система может находиться в таком состоянии сколь угодно долго. Это состояние является положением равновесия.

2. 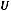>0, и, следовательно, экстремум является минимумом. Поскольку

сила F при x ≠ 0 стремится вернуть систему к положению равновесия, то равновесие является устойчивым. Движение системы в окрестности устойчивого равновесия является периодическим, хотя и не всегда гармоническим.

3. Гармонический характер движение приобретает, когда зависимость потенциальной энергии от координаты мало отличается от параболической. Это выполняется, если смещение x от положения минимума столь мало, что

.

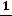
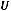
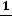
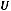
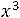Таким образом, практически в любой системе малые колебания в окрестности устойчивого равновесия являются гармоническими. Этот факт определяет особую важность изучения данного вида колебаний.

Роль возвращающей силы в (10.18) играет напряжение на конденсаторе. После очевидных преобразований приводим уравнение (10.18) к виду

(10.19)

совпадающему с уравнением (10.5) при замене q → x и

(10.20)

66

Формула (10.20) определяет частоту собственных колебаний в идеальном электрическом контуре и называется формулой Томпсона. Решение уравнения (10.19) имеет вид

(10.21)

Сила тока в цепи I, как и величина заряда q, гармонически зависит от времени, поскольку

(10.22)

где введено обозначение для амплитуды силы тока I0 = ωq0.

ЭНЕРГИЯ ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА. Поскольку энергия системы

является одной из основных ее физических характеристик, важно определить ее составляющие и зависимость от времени. Начнем с механических колебаний пружинного маятника. Зная зависимость смещения осциллятора от времени (10.6), можно легко определить зависимость от времени его скорости:

(10.23)

и кинетической энергии от времени:

(10.24)

В последнем равенстве учтено, что в соответствии с уравнением (10.4)

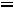
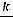. С другой стороны потенциальная энергия имеет вид

(10.25)

Следовательно, полная механическая энергия осциллятора не зависит от времени:

(10.26)

Поскольку в системе действует только консервативная упругая сила, это утверждение является еще одним случаем прямого подтверждения общего закона сохранения механической энергии.

Как видно из уравнений (10.24), (10.25) и (10.26), максимальные значения кинетической и потенциальной энергий совпадают и равны полной энергии осциллятора

,

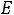
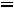
а энергия периодически полностью переходит из одного вида в другой.

График зависимости потенциальной (сплошная жирная линия), кинетической (сплошная тонкая линия) и полной энергии (прямая линия) от t при α =π/3, ω = 2π приведен на рис. 10.5. Масштаб по оси ординат выбран так, что полная энергия осциллятора равна единице.

67

Глава 11. Сложение гармонических колебаний и векторные диаграммы

СЛОЖЕНИЕ КОЛЕБАНИЙ. До сих пор мы имели дело с отдельными гармоническими колебаниями. В физике и технике часто встречаются ситуации, когда происходит сложение двух и более гармонических колебаний одинаковой частоты и одинакового направления. Если эти колебания не влияют друг на друга, то математически эта задача ставится как задача о сложении колебаний, заданных уравнениями отдельных колебаний:

(11.1)

Результирующее колебание является в этом случае суммой отдельных колебаний: x = x1 + x2. Оно, очевидно, имеет ту же частоту, что и складываемые колебания, и может быть записано в виде

(11.2)

Для нахождения результирующего колебания необходимо выразить его амплитуду x0 и начальную фазу α через амплитуды x01, x02 и фазы α1, α2 исходных колебаний. Можно решить эту задачу с помощью тригонометрических соотношений.

Более общие и эффективные подходы основаны на описании гармониче-

ских колебаний с помощью векторной амплитуды или комплексного представления гармонических колебаний.

ВЕКТОРНАЯ АМПЛИТУДА. Введение понятия векторной амплитуды основано на связи гармонических колебаний и равномерного вращения. Его суть состоит в том, что смещение при гармоническом колебании можно представить как проекцию равномерно вращающегося вектора длиной x0 на фиксированную ось, лежащую в плоскости вращения. Проекция задается функцией x = x0cos (ωt + α), в которой аргумент ωt + α соответствует равномерно увеличивающемуся со временем углу поворота вектора относительно оси. Одному обороту вектора соответствует одно колебание, а угловая скорость его вращения совпадает с частотой колебаний.

Для формализации этой идеи выберем произвольно полярную ось и построим вектор x1, называемый векторной амплитудой первого колебания, по следующим правилам (рис. 11.1):

1.Угол между осью и x1 равен начальной фазе α1 первого колебания.

2.Длина вектора x1 равна амплитуде x01 первого колебания.

Если равномерно вращать вектор x1 против часовой стрелки с угловой скоростью ω, то угол между полярной осью и векторной амплитудой будет равен (ωt + α1). Проекция вектора на ось равна x01cos (ωt + α1) и совпадает со смещением x1. Таким образом, вращающийся вектор x1 представляет гармоническое колебание.

69

t

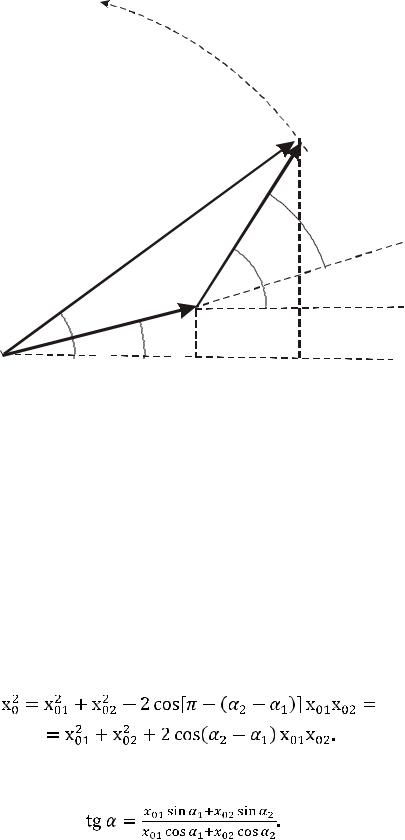
Рис. 11.1. Векторная диаграмма сложения двух гармонических колебаний

СЛОЖЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ОДИНАКОВОЙ ЧАСТОТЫ И

НАПРАВЛЕНИЯ. Отложим векторную амплитуду x2 от конца вектора x1 (рис. 11.1) в момент времени t = 0. Поскольку проекция на ось вектора x2, вращающегося вместе с x1, равна x02cos(ωt + α1), то проекция вектора x = x1 + x2 описывает суммарное колебание. Результат графического сложения векторных амплитуд называется векторной диаграммой. Таким образом, сумма векторных амплитуд складываемых колебаний представляет собой векторную амплитуду суммарного колебания. Частоты складываемых колебаний одинаковы, вследствие чего треугольник ОDВ, показанный на рис. 11.1, с течением времени не деформируется. Применяя теорему косинусов к треугольнику ОDВ, получаем для квадрата амплитуды x0 следующее выражение:

(11.3)

Из треугольника ОСВ получаем соотношение для начальной фазы α результирующего колебания:

(11.4)

БИЕНИЯ. Тем же методом может быть исследована и картина сложения колебаний двух различных частот ω и ω + ω. Поскольку в этом случае отрезки ОD и DВ вращаются с различными скоростями, треугольник ОDВ перестает

70