2701

чения g(x) > 0 аппроксимируются разложениями в ряд Тейлора, что позволяет получить совокупность полупространств:

( ): ( )+ Т( )( − ) ≥ 0, = 1, . (3.19)

На следующем шаге решается задача линейного программирования на многограннике D1, представляющем пересечение многогранника D0 и совокупности полупространств

(3.19):

min{ },

где

=( ) .

Продолжая аналогичным образом после проведения k- ой итерации получим последовательность оптимальных решений (х1, ..., хk) совокупности задач линейного программирования. Тогда на (k + 1)-й итерации исходная задача (3.15) сводится к задаче линейного программирования:

С ростом числа итераций аппроксимирующая область Dk все ближе приближается к выпуклой границе области допустимых решений D в той ее части, где находится точка ло-

51

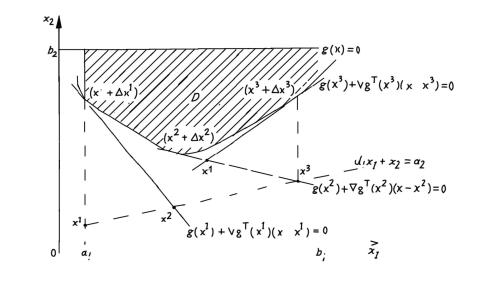
кального минимума х* исходной задачи выпуклого программирования (рис. 3.1).

Рис. 3.1. Построение отсекающих плоскостей для задачи выпуклого программирования: {minx2 при условии, что

g(x) ≥ 0; a1 ≤ x1 ≤ b1; a2 ≤ x2 ≤ b2}

Процесс поиска оптимального решения х* считается законченным, если точка текущего приближения хk принадлежит области допустимых решений D с заданной точностью:

ных неравенств, число ограничений в задаче линейного программирования (3.20) все время расчет. На практике не обязательно вводить в задачу (3.20) все m новых ограничений. На

52

(k+1)-й итерации достаточно добавлять в качестве дополнительного ограничения только одно неравенство:

( ) + Т( )( − ) ≥ 0,

индекс j для которого определяется из условия:

( ) = min ( ).

Другой подход к построению совокупности аппрокси-

Так же, как в алгоритме F25, на первой итерации (k = 1) аппроксимирующая область D0 задается в виде многогранника (3.17). Затем определяется так называемая "внутренняя"

точка В ∩ такая, что в ней строго выполняются все ограничения исходной задачи выпуклого программирования

(3.15):

( В) > 0, = 1, .

Последующие итерации (k = 2, 3, ...) алгоритма F26 сводятся к следующей последовательности действий:

1. Для задачи линейного программирования

ого ограничения, индекс которого был определен на предыдущем шаге:

+ Т − = 0.

4. Определяется аппроксимирующая область Dk+1, являющаяся пересечением области Dk и полупространства

Принимается k = k + 1 и все вычисления повторяются с шага 1.

5. Процесс поиска оптимального решения х* исходной задачи выпуклого программирования (3.15) считается законченным, если точка принадлежит области допустимых решений с заданной точностью:

На рис. 3.2 показаны четыре первых итерации построения опорных плоскостей для задачи выпуклого программирования:

min {x2}

при условии, что

g(x) ≥ 0; a1 ≤ x1 ≤ b1; a2 ≤ x2 ≤ b2.

При некоторых модификациях метод опорной гиперплоскости может быть применен для решения задачи невыпуклого программирования (минимизации линейной формы, заданной на невыпуклом множестве допустимых решений D).

54

Рис. 3.2. Построение опорных плоскостей для задачи выпуклого программирования: { minх2 при условии, что g(x) ≥

0; a1 ≤ x1 ≤ b1; a2 ≤ x2 ≤ b2 }

3.2. Сведение задачи нелинейного программирования к последовательности задач безусловной оптимизации

Задачи линейного программирования можно свести к последовательности задач безусловной оптимизации с помощью функций штрафов.

Рассмотрим класс алгоритмов , которые позволяют решение задачи выпуклого программирования (3.1) - (3.2) свести к решению последовательности задач безусловной оптимизации. В общем виде такое преобразование осуществляется при помощи специальным образом сконструированной функции, называемой штрафной функцией (функцией нагружения):

55

где сk> 0 - параметр штрафа;

(x) - индикаторная функция, имеющая следующий

вид:

R(x, ck) - функция штрафа;

- положительное большое число.

Таким образом, исходная задача выпуклого программирования (3.1) - (3.2) эквивалентна задаче безусловной оптимизации:

56

ленной, что приводит к тому, что структура минимизируемой функции Ф(x, ck) приобретает овражный характер. Следует

снижается точность определения оптимального решения х* исходной задачи (3.1) - (3.2). В связи с этим при преобразовании задачи нелинейного программирования к последовательности задач безусловной оптимизации целесообразно рас-

т.е. влияние функции штрафа R (х, сk) должно постепенно ослабевать, а последовательность оптимальных реше-

или, учитывая соотношение (3.24), для множителей Лагранжа ui можем записать:

58

= ⁄ ( ), = 1, .

Подставляя полученные значения ui в последние соотношения условий Куна-Таккера, получаем следующее равенство:

Выражение (9.26) соответствует необходимому условию существования минимума многопараметрической функции следующего вида:

будет всегда находиться внутри области допустимых решений D, так как штраф R(х, сk) = сk (х) как бы ставит "барьер" против ее выхода за границы области D. Это свойст-

59

во штрафной функции (3.27) позволяет называть ее также барьерной функцией. При уменьшении параметра сk ослабевает влияние функции штрафа R (х, сk) и возрастает влияние критерия Q(x) на значение барьерной функции Ф(х, сk). В связи с чем, при → 0 уменьшение функции Ф(х, сk) возможно только за счет минимизации функции Q(x) без нарушения ограничений (3.2) (рис. 3.4).

Предположим, что первое соотношение условий КунаТаккера не выполняется, т.е. равно не нулю, а некоторому значению ak:

( ) = , = 1, .

Тогда множители Лагранжа при условии, что gi(x) = 0 имеют вид:

ui = ak / gi(x), = 1,

Подставляя полученные значения ui в последние соотношение условий Куна-Таккера, получаем:

Выражение (3.29) соответствует необходимому условию существования минимума многопараметрической функции следующего вида:

60