
2644
.pdf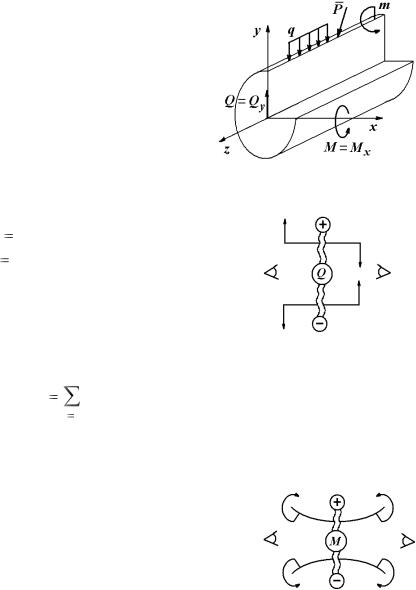
являются сечения, в которых приложены сосредоточенные силы или сосредоточенные моменты, начинается/заканчивается распределенная нагрузка (распределенные моменты), меняется геометрия сечения.
Далее будем рассматривать прямой поперечный изгиб, когда в поперечных сечениях балки возникают изгибающий момент M M x и перерезывающая сила
Q Qy (рис. 4.2).
Поперечная сила Q в сечении
балки равна алгебраической сумме проекций на вертикальную ось всех внешних сил, действующих по одну сторону от рассматриваемого сечения:
n
QPi .
i1
Рис. 4.2
Рис. 4.3
(4.1)
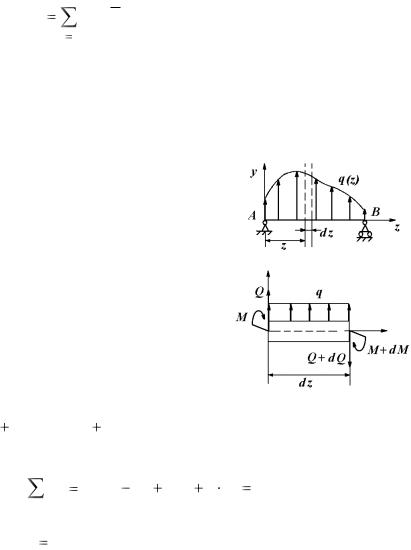
Составляющая в (4.1) положительна, если сила поворачивает отсеченную часть балки относительно рассматриваемого сечения по часовой стрелке; отрицательна – если против часовой (рис. 4.3).
Изгибающий момент M в сечении балки равен алгебраической сумме моментов всех внешних сил относительно центра тяжести рассматриваемого сечения, приложенных по одну сторону от сечения:
70
|
n |
|
M |
mO (Pi ) . |
(4.2) |
i 1
Составляющая в (4.2) положительна, если сила слева от сечения создаёт изгибающий момент, направленный по часовой стрелке, а справа – по часовой. И наоборот справа от сечения (рис. 4.4).
4.3. ТЕОРЕМЫ Д.И. ЖУРАВСКОГО
Рассмотрим произвольную двухопорную балку, находящуюся в равновесии под действием произвольной распределённой
нагрузкой (рис. 4.5). Используя |
|
|||||||
метод сечений, |
двумя |
близкими |
Рис. 4.5 |
|||||
поперечными сечениями вырежем |
||||||||
|
||||||||
элемент балки длиной dz на |
|
|||||||
расстоянии |
z от |
опоры |
A (рис. |
|
||||
4.6). В силу малости участка dz , |
|
|||||||
считаем |
нагрузку |
постоянной |
с |
|
||||
интенсивностью |
|
q . |
Действие |
|
||||
отброшенных |
частей |
заменим |
|
|||||
нагрузками |
Q |
и M |
слева |
и |
Рис. 4.6 |
|||
(Q dQ) |
и |
(M |
dM ) справа. |
Поскольку балка находится в |
||||
равновесии, то и рассматриваемый участок должен удовлетворять условиям равновесия:
|
Piy |
0 : Q (Q dQ) q dz 0 . |
||
Отсюда следует: |
||||
q |
|
dQ |
. |
(4.3) |
|
|
|||
|
|
dz |
|
|
Это 1-ая теорема Журавского в дифференциальной форме: интенсивность распределённой нагрузки на участке балки равна первой производной поперечной силы по абсциссе z .
71
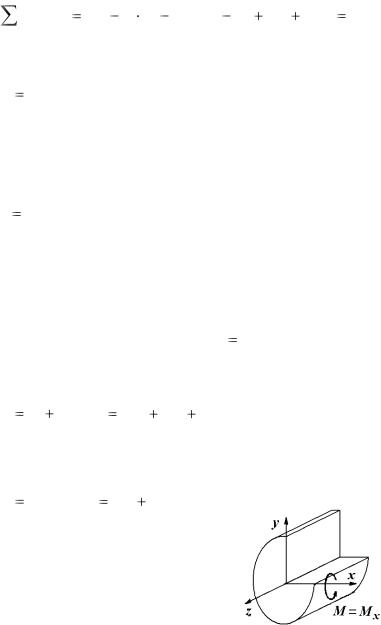
|
|
|
q(dz)2 |
||
mO (Pi ) 0 : Q dz |
|||||
|
M (M dM ) 0 . |
||||
2 |
|||||
|
|
|
|
||
Откуда, учитывая порядок малости второго слагаемого, получаем:
Q |
dM |
. |
(4.4) |
|
|||
|
dz |
|
|
Это 2-ая теорема Журавского в дифференциальной форме: поперечная сила в сечении балки равна первой производной изгибающего момента по абсциссе z .
Подставим (4.30 в (4.4):
q |
d 2M |
. |
(4.5) |
|
dz2 |
||||
|
|
|
||
Интенсивность |
распределённой нагрузки в сечении |
|||
балки равна второй производной изгибающего момента по абсциссе z .
Рассмотрим следствия этих теорем:
1) Если на участок балки действует распределённая нагрузка постоянной интенсивности q const, то поперечная
сила является линейной функцией от координаты z , а изгибающий момент изменяется по параболическому закону:
Q qz C1, M |
qz 2 |
||
|
C1z C2 . |
||
2 |
|||
|
|
||
1) Если распределённая нагрузка на участке балки отсутствует, то поперечная сила отсутствует, а изгибающий момент изменяется по линейному закону:
Qconst , M C1z C2 .
4.4.ЧИСТЫЙ ИЗГИБ
Рассмотрим случай чистого изгиба, когда в поперечных сечениях балки действует только изгибающий момент M x (рис. 4.7).
Рис. 4.7
72

4.4.1. Закон Гука при чистом изгибе
Пусть балка под действием двух равных моментов испытывает чистый изгиб (рис. 4.8). Согласно
гипотезе плоских сечений плоское поперечное сечение до деформации
остается плоским и нормальным к оси балки и после деформации. Это значит, что часть продольных волокон балки сжимается, а часть растягивается. Волокна, удлинения которых равны нулю, называют нейтральными. Их совокупность образует нейтральный слой, который пересекается с плоскостью поперечного сечения по нейтральной линии этого сечения.
Из сказанного выше следует, что закон Гука имеет такой же вид, что и при растяжении (сжатии) – нормальное напряжение прямо пропорционально деформации:
E . |
(4.6) |
4.4.2. |
Интегральные уравнения равновесия |
Выделим в |
поперечном сечении балки в окрестности |
некоторой произвольной точки А с координатами x, y
достаточно малую площадку dF , на которой действует сила, создающая нормальное напряжение . Тогда:
dMx |
y |
dF , |
(4.7) |
dM y |
x |
dF , |
(4.8) |
dN |
dF . |
(4.9) |
|
Интегрируя (4.7)–(4.9), получаем интегральные |
|||
уравнения равновесия: |
|
||
N |
dF 0 , |
(4.10) |
|
F |
|
|
|
M y |
x |
dF 0 , |
(4.11) |
|
F |
|
|
73

M x |
|
y |
|
|
dF |
|
M . |
|
|
|
|
|
|
|
|
|
|
(4.12) |
|
|||||
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4.3. Напряжения при чистом изгибе |
|
|
|||||||||||||||||||
Рассмотрим |
|
|
|
|
|
|
|
|
|
схему |
|
|
|
|
||||||||||
деформирования балки, |
испытывающей |
|
|
|
|
|||||||||||||||||||
чистый изгиб (рис. |
4.9). Ось балки |
z |
|
|
|
|
||||||||||||||||||
совпадает |
с |
положением нейтрального |
|
|
|
|
||||||||||||||||||
волокна OO1 , проходящего через центр |
|
|
|
|
||||||||||||||||||||
тяжести |
|
сечения. |
Двумя |
|
|
близкими |
|
|
|
|
||||||||||||||
|
|
|
|
Рис. 4.9 |
|
|||||||||||||||||||
поперечными |
сечениями |
|
|
|
вырежем |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
элемент балки длиной dz . Сечения в близких точках |
A и B , |
|||||||||||||||||||||||
бывшие |
|
|
до |
|
|
|
|
деформации |
|
|
|
|
|
|
|
|
||||||||
параллельными, |
|
|
после |
|
изгиба |
|
|
|
|
|
|
|
|
|||||||||||
будут пересекаться (рис. 4.10). |
|
|
|
|
|
|
|
|
||||||||||||||||
Точка |
C |
их |
|
|
пересечения |
|
|
|
|
|
|
|
|
|||||||||||
является |
|
центром |
|
|
кривизны |
|
|
|
|
|
|
|
|
|||||||||||
нейтрального |
волокна, |
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|||||||||
радиус |
кривизны |
|
нейтрального |
|
|
|
|
|
|
|
|
|||||||||||||
волокна. |
|
После |
|
|
деформации |
|
|
|
|
|
|
|
|
|||||||||||
волокно |
AB превратится в дугу |
|
|
|
|
|
|
|
|
|||||||||||||||
A1B1 . Вычислим его относительное |
|
|
|
Рис. 4.10 |
|
|
||||||||||||||||||
удлинение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
A1B1 |
AB A1B1 |
|
|
OO1 |
|
|
|
|
|
|
||||||||||||
|
|
|
AB |
|
|
|
|
|
|
OO1 |
|
|
|
|
|
|
|
|
||||||
= |
( |
|
y)d |
|
|
|
d |
|
|
y |
. |
|
|
|
|
|
|
|
(4.13) |
|
||||
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Преобразуем (4.6), (4.10)–(4.12) с учетом (4.13): |
|
|
||||||||||||||||||||||
|
|
E |
|
E |
y |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.14) |
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
E |
|
|
||||||||
N |
|
dF |
|
E |
dF |
|
ydF |
|
Sx 0 . |
(4.15) |
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
F |
|
|
|
|
|
|
F |
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74 |
|
|
|
|
|
|
|
|
|||

Т.к. Sx |
0 , то ось OO1 |
действительно является |
||||||||||||||||||
центральной, т.е. проходит через центр тяжести сечения. |
||||||||||||||||||||
M y |
|
|
|
x |
dF |
|
|
E |
xydF |
|
|
E |
J xy |
0 . |
(4.16) |
|||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
F |
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
Т.к. |
|
J xy |
0 , |
то |
ось OO1 |
является |
главной осью |
|||||||||||||
инерции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M x |
|
|
|
y |
dF |
|
E |
y2dF |
|
E |
J x |
M . |
(4.17) |
|||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
F |
|
|
|
|
|
F |
|
|
|
|
|
|
|
||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
E |
|
M |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.18) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
J x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставим (4.18) в (6.14): |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
E |
y |
M |
y . |
|
|
|
|
|
|
|
(4.19) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
J x |
|
|
|
|
|
|
|
|
|
|
|
|
|
Т.о. |
|
|
|
нормальные |
напряжения |
|
||||||||||||||
распределены по высоте балки по линейному |
|
|||||||||||||||||||
закону (рис. 4.11). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4.4.4.Расчёт на прочность при чистом изгибе
Деталь |
|
прочная, если наибольшие |
Рис. 4.11 |
||||||||
напряжения не превышают допускаемого: |
|||||||||||
|
|||||||||||
|
|
max |
[ |
] . |
|
|
(4.20) |
||||
|
|
|
|
|
|
|
|||||
С учётом (4.19) условие прочности имеет вид: |
|||||||||||
|
|
M |
|
|
ymax |
[ |
] , |
|
(4.21) |
||
|
|
|
|
|
|||||||
|
|
|
|
||||||||
|
|
|
|
|
|
||||||
|
|
J x |
|
|
|
|
|
||||
где ymax |
– |
точка сечения, |
наиболее удаленная от его |
||||||||
центра тяжести.
Осевым моментом сопротивления сечения называется величина:
75

Wx |
|
J x |
. |
(4.22) |
||||
ymax |
||||||||
|
|
|
|
|
|
|||
Тогда условие прочности примет вид: |
|
|||||||
|
|
M |
|
[ |
] . |
|
(4.23) |
|
|
|
|
|
|||||
|
|
|
|
|
||||
Wx |
|
|||||||
|
|
|
|
|||||
Из условия прочности (4.23) вытекают три вида расчетов: проверочный, проектный расчет и расчет на предельную нагрузку.
7)Проверочный расчет. Сводится к вычислению возникающих в детали напряжений и непосредственной проверке соблюдения условия (4.23).
8)Проектный расчет. Заключается в определении минимально необходимой площади поперечного сечения стержня. Для этого условие (4.23) представляется в виде:
M
Wx [ ] . (4.24)
Для балки трубчатого сечения, как было показано раньше:
J p |
|
D 4 |
(1 |
4 ) . |
|
|
|
|
||||||
32 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Учитывая, что J p |
J x J y |
и J x J y , получаем |
||||||||||||
|
|
|
|
D4 |
4 ) . |
|
|
|
||||||
J x J y |
|
|
|
|
(1 |
|
|
|
|
(4.25) |
||||
64 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Подставляя (4.25) и |
ymax |
D |
, получим: |
|||||||||||
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
J x |
|
|
|
D3 |
4 |
|
|
|
||||
Wx |
|
|
|
|
|
|
(1 |
|
) . |
|
(4.26) |
|||
|
D / 2 |
|
|
32 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Для вала трубчатого (кольцевого) сечения с учётом |
||||||||||||||
(3.14) получим: |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
J p |
|
|
|
D3 |
4 ) . |
|
|
|||||
W p |
|
|
|
|
|
|
(1 |
|
(4.27) |
|||||
|
|
|
|
|
|
|||||||||
|
|
D / 2 |
|
|
16 |
|
|
|
|
|
|
|||
76

С учетом (4.27), условие прочности (4.23) примет вид:
|
|
16 M |
|
D |
3 |
[ ](1 4 ) . |
(4.28) |
9) Расчет на предельную нагрузку. Надо определить допустимую величину нагрузки. Нагрузка будет наибольшей, когда условие (4.23) из неравенства превращается в равенство. Из него определяется допустимое значение изгибающего момента:
M Wx [ ] . |
(4.29) |
По найденному значению |
с использованием эпюры M |
или уравнений статики устанавливают допустимые значения приложенных к балке нагрузок.
Примечание. Если допускаемые напряжения на растяжение и сжатие отличаются, то условие (4.23) разбивается на два:
|
|
M |
|
|
[ ] р |
и |
|
|
M |
|
[ |
]c , |
(4.30) |
|
max |
|
|
|
|
min |
|
|
|
||||||
Wxр |
Wxc |
|||||||||||||
|
|
|
|
|
|
|
||||||||
где [ ] р и |
[ ]c |
– |
допускаемые |
напряжения на |
||||||||||
растяжение и сжатие.
4.4.5.Коэффициент экономичности
Вформуле (4.28) критерия прочности
M
Wx
[ ]
осевой момент сопротивления стоит в знаменателе, следовательно, с увеличением момента сопротивления увеличивается и прочность балки. Поэтому с точки зрения экономии материала наиболее рациональными будут такие сечения, у которых при малой площади моменты сопротивления получаются большими. Так, например, прямоугольное сечение балки, выгоднее, чем квадратное. Балка прямоугольного сечения, положенная плашмя, будет иметь
77

момент сопротивления момент сопротивления меньше, следовательно, класть балку плашмя невыгодно. Для оценки экономичности детали используют коэффициент эффективной прочности (экономичности):
K |
Wx |
. |
(4.31) |
|
|
|
|||
 F 3
F 3
Прямоугольное и круглое сечения чаще всего встречаются в деревянных балках. Для металлических балок выбирают другие, более рациональные сечения.
Так как вблизи от нейтральной оси материал мало напряжен, то выгоднее больше материала сосредоточивать подальше от нейтральной оси, т.е. переносить его от мест, где он напряжен мало, к местам, где он будет напряжен больше.
Существует ряд сечений балок, обладающих наибольшей прочностью при наименьшем весе: двутавр, швеллер, уголок неравнобокий, уголок равнобокий, тавр (рис. 4.12). Часто применяют сварное соединение профилей.
Рис. 4.12. а) двутавр, б) швеллер, в) уголок неравнобокий, г) уголок равнобокий, д) тавр,
е) сварное соединение профилей
Поэтому для балок из металла, сопротивляющегося одинаково растяжению и сжатию, часто сечения выбирают в виде двутавра, швеллера; применяются сварные балки. Такие балки в сравнении с балками прямоугольного и круглого сечений, имеющими такую же площадь сечения, дают значительно большие моменты сопротивления. Нейтральная
78

линия в этих сечениях проходит посредине высоты, поэтому наибольшие напряжения растяжения и сжатия для таких сечений будут одинаковыми. Для балок, материал которых сопротивляется неодинаково растяжению и сжатию, например чугун, берутся сечения, несимметричные относительно нейтральной линии, как, например, тавровое сечение (рис. 4.12). Тавр тогда располагают так, чтобы в горизонтальной полке были напряжения растяжения; последние благодаря приближению нейтральной оси к горизонтальной полке оказываются меньшими напряжений сжатия.
На практике нередко встречается кольцевое (трубчатое) сечение. Момент сопротивления кольцевого сечения больше, чем круглого сечения равной площади, так как материал в кольцевом сечении более рационально использован: он отнесен дальше от нейтральной линии.
Моменты инерции и моменты сопротивления катаных профилей стандартных размеров задаются в таблицах сортамента ГОСТ.
4.5. ПОПЕРЕЧНЫЙ ИЗГИБ
Рассмотрим более подробно случай поперечного изгиба, когда в поперечных сечениях балки возникают
изгибающий момент |
M M x и |
|
перерезывающая сила Q |
Qy (рис. 4.13). |
Рис. 4.13 |
4.5.1. Напряжения при поперечном изгибе. Формула Журавского
Пренебрегая силами трения между волокнами изогнутой балки, будем считать, что гипотеза плоских сечений условно выполняется (хотя небольшая депланация присутствует). Нормальное напряжение:
|
M |
|
|
y . |
(4.32) |
|
|
||||
|
|
|
|
||
|
J x |
|
|||
79
