2569

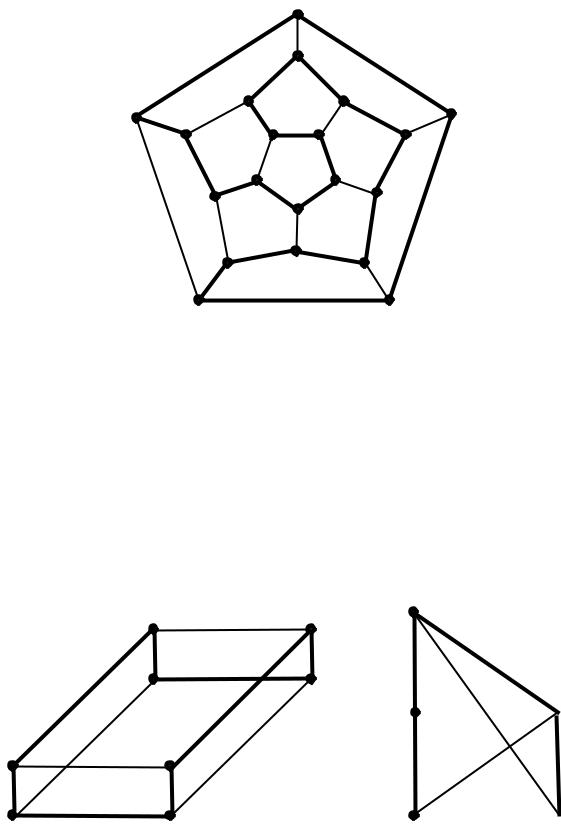
ходящего через каждую вершину по одному разу (рис. 74)), определив тем самым класс графов, носящих теперь его имя.

Граф называется гамильтоновым, если он имеет простой цикл, проходящий через все вершины графа, т.е. цикл, в котором попарно различны все вершины графа, кроме первой и последней. Сам такой цикл также называется

гамильтоновым.

Простые цепи, проходящие через все вершины графа, также называются гамильтоновыми, если они включают в себя все попарно различные вершины графа.

Примерами гамильтоновых графов могут служить графы, изображенные на рис. 74 и рис. 75. На этих рисунках жирными линиями выделены гамильтоновы циклы.

Рис. 75. Гамильтоновы графы

71

Ответить на вопрос, является ли граф гамильтоновым, непросто, так как необходимого и достаточного условия существования гамильтонова цикла (как теорема 11.2 для эйлеровых графов) нет. Однако, имеются достаточные условия существования гамильтоновых циклов. Приведем некоторые из них, применимые к связным неорграфам без петель, имеющим n ≥3 вершин.

Теорема 11.3 (Оре*). Если в графе степени любых двух несмежных вершин υi и υj удовлетворяют неравенству δ (υi )+δ (υj )≥ n , то граф гамильто-

нов.

Теорема 11.4 (Дирака*). Если степень любой вершины графа удовлетво-

ряет неравенству δ (υi )≥ n2 , то граф гамильтонов.

Для орграфов также имеется достаточное условие.

Теорема 11.5 (Гуйя-Ури). Если для любой вершины сильно связного

циклом.

Орграф называется полугамильтоновым, если он содержит гамильтонову цепь.

Задача нахождения гамильтоновых циклов получила свое развитие в связи с рядом практических задач. Одной из них является так называемая задача о коммивояжере, в которой определяется кратчайший гамильтонов цикл. Решение этой задачи будет описано в главе 13.

* Биографические сведения см. в прил. 2.

72

12.Деревья

12.1.Основные определения

Граф T называется деревом, если он связный и не имеет циклов (рис. 76). Лесом называется граф, связные компоненты которого являются деревь-

ями (рис. 77).

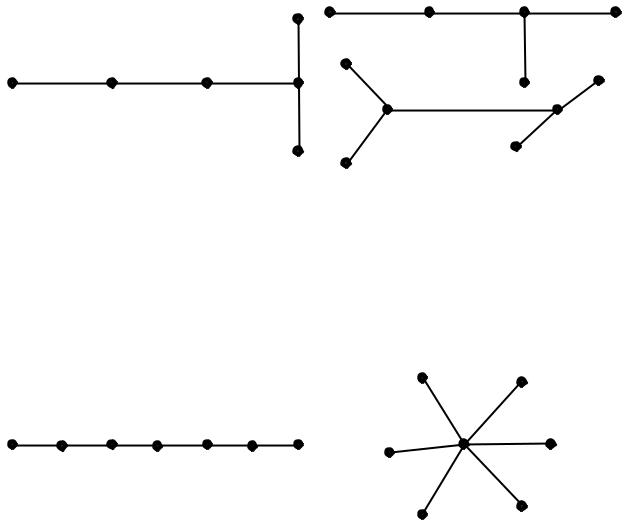
Рис. 76. Дерево

Рис. 77. Лес

Дерево не может иметь петель и кратных ребер. Среди деревьев выделяют два частных случая:

●последовательное дерево, представляющее собой простую цепь

(рис. 78);

●звёздное дерево, являющееся «кустом», в котором одна из вершин (центр) является смежной со всеми остальными (рис. 79).

Пусть носитель графа V содержит n вершин. Если связать эти вершины рёбрами так, чтобы отсутствовал цикл, то получится дерево. Для двух вершин существует одно дерево: сами эти вершины и связывающее их ребро. С увеличением числа вершин n число различных деревьев Tn быстро увеличивается и

их количество можно найти, воспользовавшись теоремой Кэли.

Теорема 12.1 (Кэли). Число деревьев с n занумерованными вершинами

равно

73

Деревья считаются различными, если они не изоморфны (впрочем, как и любые графы). Например, деревьев с 4 вершинами всего 16 , из них существенно различаются только 2 . Деревьев с 6 вершинами будет 1296 , и только 6 будут существенно различаться.

Следует отметить, что среди графов порядка n полный граф имеет максимальное количество рёбер, а дерево – минимальное количество рёбер, необходимых для того, чтобы граф был связным.

12.2. Свойства деревьев

Сформулируем свойства деревьев в виде теорем.

Теорема 12.2. Каждое дерево с n вершинами имеет (n −1) ребер.

Доказательство. Две любые вершины дерева связаны одним ребром. Для связи существующей вершины с каждой из добавляемых вершин нужно ещё одно ребро. Если добавить два ребра, т.е. соединить новую вершину с двумя уже рассмотренными вершинами, то обязательно образуется цикл. Следовательно, для связи n вершин необходимо (n −1) ребро.

Теорема 12.3. Граф является деревом тогда и только тогда, когда каждая пара различных вершин графа соединяется только одной простой цепью.

Теорема 12.4. У каждого дерева найдётся висячая вершина.

Теорема 12.5. При удалении любого ребра дерева (рис. 80,а) оно распадается на связные компоненты, которые являются деревьями, т.е. образуется лес (рис. 80,б). При добавлении любого нового ребра образуется цикл и дерево перестаёт быть деревом (рис. 80,в).

Замечание 12.1. Из любого связного графа, не являющегося деревом, можно удалить некоторые рёбра, не нарушая связности (например, ребро, входящее в цикл).

74

12.3. Типы вершин дерева и его центры

Рассмотрим дерево T с n вершинами. Назовём его концевые (висячие) вершины вершинами типа 1. Если удалить все концевые вершины и рёбра дерева T , то получим связный граф без циклов T1 , т.е. получим опять дерево, но

уже с меньшим количеством вершин и рёбер. Концевые вершины дерева T1 на-

зываются вершинами типа 2 дерева T . Аналогично определяются вершины типа 3, типа 4 (рис. 81) и т.д. Ясно, что дерево может иметь одну или две вершины максимального типа.

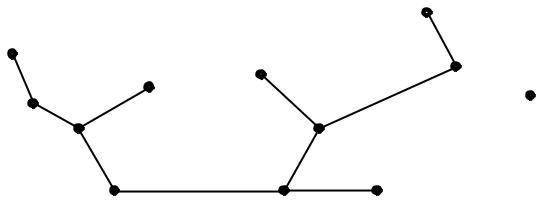
Рис. 81. Типы вершин дерева

Пусть вершина типа K есть вершина максимального типа. Из определения типа вершин следует, что эксцентриситет вершины максимального типа (если она одна) равен K −1, а эксцентриситет каждой из двух вершин максимального типа равен её типу, т.е. равен K . При этом эксцентриситет любой вершины не максимального типа будет всегда больше ее типа и больше эксцентриситета вершины максимального типа.

Следовательно, центрами любого дерева являются его вершины мак-

симального типа, и поэтому дерево может иметь или один, или два центра.

Кратчайшая диаметральная цепь дерева проходит через его центр или оба центра, если их два. В первом случае длина диаметральной цепи равна 2K −2 , а во втором 2K −1.

Например, дерево на рис. 81 имеет два центра (вершины типа 4), а кратчайшая диаметральная цепь состоит из 2K −1 = 2 4 −1 = 7 ребер.

12.4. Корневые деревья

Произвольно зафиксируем некоторую вершину υ0 дерева T и назовём её

корнем дерева. Тогда само дерево называется деревом с корнем или корневым

деревом.

Из статических соображений в дереве удобно выделить некоторую цепь,

75

выходящую из корня. Такую цепь называют стволом дерева. Как правило, корень дерева является концевой вершиной ствола.

Каждая концевая вершина связана с ближайшей вершиной в стволе единственной цепью, называемой ветвью дерева, исходящей из одной вершины и заходящей в другую.

При отсутствии у дерева ствола ветвями дерева называются цепи, связывающие концевые вершины дерева с его корнем.

Висячие вершины в дереве называют листьями, а все остальные – внутренними вершинами.

Корневые деревья могут быть как неориентированными, так и ориентированными (от корня или к корню).

Ориентированное дерево называется прадеревом с корнем υ0 , если су-

ществует простой путь от этой вершины до любой другой вершины прадерева. Ориентированное дерево можно получить из неориентированного дерева (рис. 82) следующей процедурой его ориентации. Выберем произвольную вершину дерева – корень. Все рёбра, инцидентные корню дерева, считаем исходящими из корня и заходящими в соответствующие им инцидентные вершины. Все рёбра, инцидентные вершинам, удалённым на расстояние 1 от корня, считаются исходящими из этих вершин и заходящими в смежные им вершины. Процесс ориентации рёбер продолжают до тех пор, пока не будут ориентированы все рёбра дерева. Полученное таким образом корневое дерево называется ориентированным деревом (рис. 83). Все рёбра в нем имеют направление от

корня. Очевидно, что прадерево может иметь только один корень.

Следует отметить, что для любой вершины ориентированного корневого дерева, кроме корня, полустепень захода δ −(υi )=1. Для корня полустепень за-

хода δ −(υ0 )= 0, а для листьев полустепень исхода равна нулю.

υ0

Рис. 82. Неориентированное корневое дерево

76

вершинами графа G , то говорят, что дерево T покрывает граф G . В этом случае дерево Т называют остовом (каркасом) или покрывающим деревом графа

G .

В дальнейшем нам потребуется понятие матрицы Кирхгофа. Матрицу Кирхгофа K можно получить как разность диагональной матрицы F , диагональные элементы которой равны степеням вершин ( fii =δ(υi )), и матрицы

Матрица Кирхгофа обладает свойством: сумма элементов в каждой

строке и каждом столбце равна нулю.

Количество остовов (каркасов) неорграфа G можно найти, воспользовавшись следующей теоремой.

Теорема 12.7 (Кирхгофа). Число остовов неорграфа равно алгебраическому дополнению любого элемента матрицы Кирхгофа.

Пример 12.1. Определить количество остовов мультиграфа, изображённого на рис. 85.

υ2 υ3

Рис. 85. Мультиграф

Решение. Матрица смежности B данного мультиграфа имеет вид

78

Следуя теореме 12.7, определим количество остовов мультиграфа, изображённого на рис. 85. Вычислим алгебраическое дополнение любого элемента матрицы Кирхгофа, например для элемента k44 :

Следовательно, у данного мультиграфа имеется 13 различных остовов.

Количество остовов можно определить и для орграфа. Остовом орграфа можно считать остов его основания.

Рассмотрим две матрицы, которые получаются аналогично матрице Кирхгофа.

Пусть G – орграф с матрицей смежности В. Тогда матрицы K + и K − определим как

где F + и F − – диагональные матрицы, у которых диагональные элементы рав-

ны полустепеням исхода ( fii+ =δ +(υi )) и полустепеням захода ( fii− =δ −(υi ) ) вершин соответственно.

79

Теорема 12.8. Число остовов орграфа, входящих в вершину υi , равно ал-

гебраическому дополнению любого элемента i-й строки матрицы K + . Число остовов орграфа, выходящих из вершины υi , равно алгебраическому дополне-

нию любого элемента i-го столбца матрицы K − .

Пример 12.2. Определить количество остовов орграфа, изображённого на рис. 86, входящих в вершину υ1 и выходящих из нее.

υ1 υ2

υ3

υ5 υ4

Рис. 86. Орграф

Решение. Матрица смежности B орграфа имеет вид

Найдем полустепени исхода и полустепени захода вершин орграфа и составим диагональные матрицы F +, F − и матрицы K + и K − .

Так как δ +(υ1 )= 2 , δ +(υ2 )= 2 , δ +(υ3 )=1, δ +(υ4 )= 2 и δ +(υ5 )=1, то

80