2569

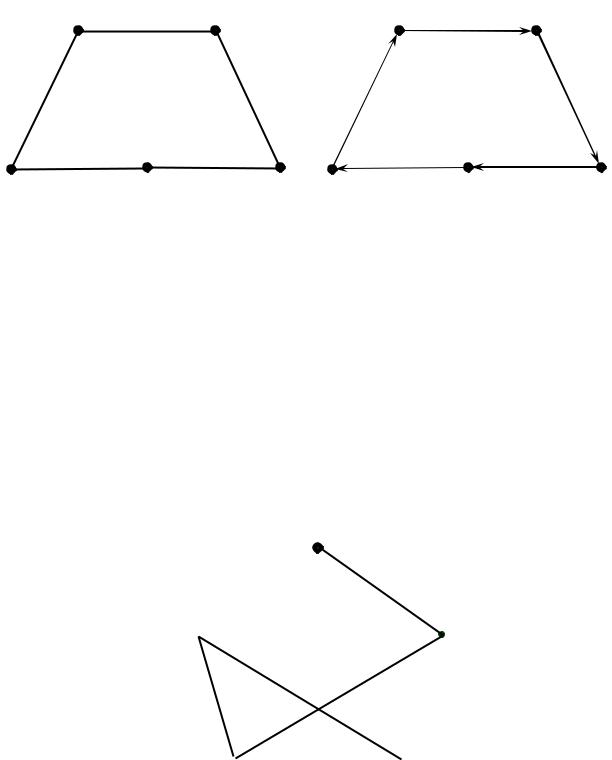
Замкнутый маршрут, в котором попарно различны все вершины, кроме первой и последней, называется простым циклом (рис. 50) в неорграфе и про-

стым контуром (рис. 51) в орграфе.

8.2.Выявление маршрутов в графе заданной длины

Спомощью матрицы смежности можно найти в графе маршруты заданной длины. Это отражено в следующей теореме.

Теорема 8.1. Если В – матрица смежности графа G без петель, то элемент

βij матрицы BK ( K N ) равен количеству маршрутов длины К от вершины υi к вершине υj .

Пример 8.1. Вычислить количество циклических маршрутов длины 3 в графе, изображённом на рис. 52, и показать их.

υ1

υ2 υ5

υ4υ3

Рис. 52. Неорграф

41

Решение. Составим матрицу смежности данного неорграфа.

Для того чтобы найти все маршруты в графе длины 3, необходимо его матрицу смежности возвести в третью степень, т.е. найти B3 = B B B .

Сначала вычислим B2 :

Чтобы найти в графе (см. рис. 52) все циклические маршруты длины 3, требуется сложить элементы, стоящие на главной диагонали матрицы B3 :

β11 + β22 + β33 + β44 + β55 = 0 + 2 + 2 + 4 + 4 =12 .

Таким образом, циклических маршрутов длины 3 с начальной вершиной υ1 не существует (см. рис. 52), с начальной вершиной υ2 и υ3 по два

(υ2 −υ5 −υ4 −υ2 , υ2 −υ4 −υ5 −υ2 и υ3 −υ5 −υ4 −υ3 , υ3 −υ4 −υ5 −υ3 ), а с на-

чальной вершиной υ4 и υ5 по четыре (υ4 −υ2 −υ5 −υ4 , υ4 −υ5 −υ2 −υ4 ,

42

Пример 8.2. Вычислить количество маршрутов длины 2, 3 и 4 в графе, изображённом на рис. 53, из вершины υ3 в υ2 и показать их.

υ1υ2

υ4 υ3

Рис. 53. Орграф

Решение. Как и в примере 8.1, сначала составим матрицу смежности:

а затем найдем B2 , B3 и B4 , так как нам необходимо вычислить количество маршрутов длины 2, 3 и 4.

Итак, вычислим B2 :

Теперь найдем B3 :

43

Этап 1. Нахождение длины кратчайшего пути

Шаг 1. Присвоение вершинам начальных меток

Полагаем d (s)= 0* и считаем эту метку постоянной (постоянные метки будем помечать сверху звездочкой). Для остальных вершин υi V , υi ≠ s по-

лагаем d (υi )= ∞ и считаем эти метки временными. Пусть υ = s , где υ – обозначение текущей вершины.

Шаг 2. Изменение меток

Для каждой вершины υi с временной меткой, непосредственно следующей за вершиной υ, меняем ее метку в соответствии со следующим правилом:

где w(υ,υi ) – вес дуги, соединяющей вершины υ и υi .

Шаг 3. Превращение метки из временной в постоянную

Из всех вершин с временными метками выбираем вершину υi*0 с наименьшим значением метки:

где d (υi ) – временная метка (υi V ).

Превращаем эту метку в постоянную и полагаем υ =υi*0 .

Шаг 4. Проверка на завершение первого этапа

Если требуется найти кратчайший путь в вершину t, условием окончания алгоритма является пункт 4а. Если ищутся кратчайшие пути во все вершины, то условие окончания – 4б.

4а. Если υ =t , то d (υ) – длина кратчайшего пути от s до t. В противном

случае происходит возвращение ко второму шагу.

4б. Если все вершины имеют постоянные метки (значения этих меток будут показывать длины кратчайших путей), то необходимо закончить алгоритм. В противном случае вернуться ко второму шагу.

Этап 2. Построение кратчайшего пути

Шаг 5. Последовательный поиск дуг кратчайшего пути

Среди вершин, непосредственно предшествующих вершине υ с постоянными метками, находим вершину υi (удовлетворяющую соотношению):

47

Включаем дугу, соединяющую вершины υi и υ, в искомый путь и полагаем υ =υi .

Шаг 6. Проверка на завершение второго этапа

Если υ = s , то кратчайший путь найден – его образует последовательность дуг, полученных на пятом шаге и выстроенных в обратном порядке. В противном случае возвращаемся к пятому шагу.

Пример 8.5. По алгоритму Дейкстры найти кратчайший путь от вершины s =υ1 до вершины t =υ6 во взвешенном орграфе, заданном матрицей весов:

Решение. Данный взвешенный орграф содержит шесть вершин: υ1,υ2,υ3,υ4,υ5, υ6 . Как видно из матрицы весов (по первой строке), вершина υ1

соединена с вершинами υ2,υ3,υ4 и υ5 и длины дуг, соединяющих вершину υ1 с υ2,υ3,υ4,υ5 , соответственно равны 5, 11, 3 и 15. Петли в вершине υ1 нет, так как элемент w11 = 0. Вершина υ1 с υ6 не соединена ( w16 = ∞). Аналогично рас-

суждая о значениях элементов в остальных строках, изобразим взвешенный орграф, соответствующий данной матрице весов (рис. 55).

15

Рис. 55. Взвешенный орграф

48

Применим алгоритм Дейкстры.

Этап 1. Нахождение длины кратчайшего пути

Шаг 1. Присвоение вершинам начальных меток

Полагаем d (s)= 0* – постоянная метка, υ = s =υ1 – текущая вершина,

d (υ2 )= d (υ3 )= d (υ4 )= d (υ5 )= d (υ6 )= ∞ – временные метки.

Все результаты вычислений удобно приводить в виде таблицы. После первого шага получаем табл. 1.

Таблица 1

1-я итерация

Шаг 2. Изменение меток

Множество вершин, непосредственно следующих за υ = s =υ1 с временными метками V ={υ2,υ3,υ4,υ5}. Пересчитываем временные метки этих вершин:

Шаг 3. Превращение метки из временной в постоянную

Одна из временных меток превращается в постоянную

min{d (υ2 ), d (υ3 ), d (υ4 ), d (υ5 ), d (υ6 )}= min{5,11, 3,15, ∞} =3 = d (υ4 ),

принимаем за υ =υ4 .

Шаг 4. Проверка на завершение первого этапа

υ =υ4 ≠ t =υ6 ,

происходит возвращение на второй шаг.

49

Результаты вычислений оформим в виде табл. 2.

Таблица 2

2-я итерация

Шаг 2

Множество вершин, непосредственно следующих за υ =υ4 с временными метками V ={υ5,υ6}. Пересчитываем временные метки этих вершин:

dнов. (υ5 )= min{dстар. (υ5 ), d (υ)+ w(υ,υ5 )}= min{15, 3* +6}= min{15, 9}=9 ,

dнов. (υ6 )= min{dстар. (υ6 ), d (υ)+ w(υ,υ6 )}= min{∞, 3* + 20}= min{∞, 23}= 23.

Шаг 3

Одна из временных меток превращается в постоянную:

min{d (υ2 ), d (υ3 ), d (υ5 ), d (υ6 )}= min{5,11, 9, 23} =5 = d (υ2 ),

принимаем за υ =υ2 .

Шаг 4

υ =υ2 ≠ t =υ6 ,

происходит возвращение на второй шаг. Результаты вычислений приведем в табл. 3.

Таблица 3

3-я итерация

Шаг 2

Множество вершин, непосредственно следующих за υ =υ2 с временными метками V ={υ3} (у вершины υ4 есть постоянная метка). Пересчитываем временную метку этой вершины:

50