
2444
.pdf
Рис. 2.5. Расстояние вдоль перпендикуляра от точки (Х, у) до прямой легко определяется как только найдена ближайшая к ней точка прямой (Х0, у0).
Можно представить следующим образом: х0 = -psinΘ + scosΘ и
y0= +pcosΘ + ssinΘ, где s - расстояние вдоль прямой, отсчитываемое от ближайшей к началу координат точки.
Чтобы можно было вычислить расстояние r от каждой данной точки объекта с
координатами (х, у), нам нужно найти ближайшую к ней точку на прямой (х0, у0) (рис. 2.5). Тогда r2 = (х - х0)2 + (у – у0)2.
Подставляя сюда значения х0 и у0 из параметрических уравнений, получим r2 = (х2 +
у2)+ р2 + 2p(xsinΘ - ycosΘ) - 2s(xcos0 + ysin0) + s2. Дифференцирование по s и
приравнивание результата нулю дают выражение s = xcosΘ + ysinΘ. Это выражение в свою очередь необходимо подставить в параметрические уравнения для х0 и у0. Из них мы сможем найти разности х - х0 = +sinΘ (xsinΘ – ycosΘ + р),
у - yо= -cos Θ (хsinΘ - уcosΘ + р) и, следовательно, r2 = (хsinΘ – ycosΘ + р)2. Сравнивая этот результат с уравнением прямой, видим, что прямая есть геометрическое место точек, для которых r = 0! Более того, становится очевидным преимущество выбранного нами способа параметризации прямой: расстояние до прямой мы получаем непосредственно.
Теперь перейдем к минимизации интеграла
E |
(x sin |
y cos |
p)2 b(x, y)dxdy |
|
I |
|
|
Дифференцирование по р |
и приравнивание результата нулю приводят к уравнению |
||
A(x sin |
y cos |
p) 0 , где ( x , y ) - определенные выше координаты геометрического |
|
центра. |
Таким |
образом, |
90 |
ось минимального второго момента проходит через |
|||
геометрический центр. Это наводит на мысль о замене переменных х' = х - x и у' = у - y ,
после чего будем иметь
xsinΘ - ycosΘ + р = x'sinΘ - у'cosΘ и, следовательно, Е = a sin2Θ - bsinΘcosΘ + сcos2Θ, где a, b и с - вторые моменты, вычисляемые по формулам:
a |
(x )2 b(x, y)dx dy , |
|
I |
b 2 |
(x y )b(x, y)dx dy , |
|
I |
c |
( y )2 b(x, y)dx dy , |
|
I |
Теперь можно переписать выражение для Е в виде
E |
1 |
(a c) |
1 |
(a c) cos2 |
1 |
bsin 2 . |
|
2 |
2 |
2 |
|||||
|
|
|
|
Дифференцируя по Θ и приравнивая результат нулю, получаем tg 2 Θ = b/(a — с), если только b≠О или а≠с. Следовательно,
sin 2 |
|
b |
|
и cos2 |
|
a |
c |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
b2 (a c)2 |
|
b2 |
(a c)2 |
|
|||
|
|
|
|
|
|
Из двух полученных решений то, которому отвечают знаки плюс в выражениях для sin2Θ и cos2Θ, дает требуемый минимум Е. И наоборот, решение с отрицательными знаками соответствует максимальному значению Е. (Это можно показать, исследовав вторую производную от Е по Θ). Если b = 0 и а = с, то оказывается, что Е не зависит от Θ. В этом случае объект слишком симметричен, чтобы описанным способом можно было определить его ось. Отношение наименьшего значения Е к наибольшему характеризует в некоторой степени, насколько «округлым» является объект. Это отношение равно нулю для прямой и единице для окружности.
91

Иной путь решения проблемы состоит в попытке найти угол поворота Θ, при котором матрица вторых моментов размера 2x2 имеет диагональный вид.
2.2. Проекции
Для вычисления положения и ориентации объекта достаточно знать первые и вторые моменты. (При этом остается двузначность в выборе направления на оси). Чтобы найти их значения, нет необходимости в исходном изображении: достаточно знать его проекции. Указанный факт представляет интерес, поскольку проекции описываются более компактно и приводят к гораздо более быстрым алгоритмам.
Рассмотрим прямую, проходящую через начало координат и наклоненную к оси х под углом Θ (рис. 2.6). Проведем новую прямую, пересекающую первую под прямым углом в точке, находящейся на расстоянии t от начала координат. Обозначим расстояние вдоль новой прямой через s. Интеграл от функции b(х, у) вдоль новой прямой дает одно значение проекции. Иными словами,
p (t) |
b(t cos |
s sin ,t sin |
s cos )ds . |
|
L |
|
|
92

Рис. 2.6. Проекция области изображения на прямую, составляющую с осью х угол Θ. Ее можно найти путем интегрирования вдоль прямых, подобных той, которая обозначена буквой L.
Интегрирование осуществляется по части прямой L, лежащей внутри изображения. Например, вертикальная проекция (Θ = 0) описывается выражением:
(x) |
b(x, y)dy , |
|
L |
а горизонтальная проекция (Θ=π/2) — выражением:
h( y) |
b(x, y)dx |
|
|||
|
|
|
L |
|
|
Далее, поскольку |
|
||||
A |
b(x, y)dxdy, |
|
|||
|
|
I |
|
|
|
имеем |
|
|
|
||
A |
(x)dx |
h( y)dy |
|
||
|
|
|
|
||
Более важно, что |
|
||||
|
|
|
xb(x, y)dxdy |
x (x)dx |
|
xA |
|||||
|
|
|
I |
|
|
и |
|
|
|
||
|
|
|
yb(x, y)dxdy |
yh( y)dy 93 |
|
|
yA |
||||
|
|
|
I |
|
|
Таким образом, первые моменты проекций равны первым моментам исходного
изображения. |
|
|
|
|
|
|
||
Чтобы |
|
найти |
ориентацию, нам |
нужны |
также |
и вторые |
моменты. |
|
Два |
из |
них |
также |
легко |
вычисляются |
с |
помощью |
проекций |
x2b(x, y)dxdy |
x2 (x)dx |
|
|
|
|
|
||
I |
|
|
|
|
|
|
|
|
y2b(x, y)dxdy |
y2h( y)dy |
|
|
|
|
|
||
I |
|
|
|
|
|
|
|
|
Р

Рис. 2.7. Горизонтальная h(y), диагональная d(t) и вертикальная v(x) проекции, содержащие всю необходимую информацию для вычисления моментов нулевого, первого и второго порядков области изображения. Эти моменты в свою очередь дают исчерпывающую информацию, которая требуется для определения положения и ориентации области.
Однако интеграл от произведения ху через введенные выше проекции вычислить
невозможно. Мы можем добавить диагональную проекцию (Θ=π/4):
94
d (t) |
b |
1 |
|
(t s), |
1 |
|
(t s) ds |
||
|
|
|
|
|
|
||||
|
|
||||||||
|
2 |
2 |
|
|
|||||
Таким образом, все интегралы, необходимые для вычисления положения и ориентации области на бинарном изображении, можно получить используя горизонтальную, диагональную и вертикальную проекции (рис. 2.7).
То, что было сейчас изложено, интересно сравнить с методами восстановления в томографии. В ней рассматриваются интегралы от поглощающей способности материала образца. Проблема состоит в восстановлении плотности распределения вещества. В методах рентгеновской томографии образец представляют в виде стопки срезов, причем каждый срез соответствует отдельной двумерной задаче. Получаемые проекции аналогичны тем, о которых шла речь выше. Можно показать, что распределение поглощающего материала определяется при наличии известных проекций для всех направлений и при условии, что плотность отлична от нуля только в ограниченной области пространства.
Какое отношение имеет восстановление в томографии к изучаемой здесь проблеме? Основное различие состоит в том, что в нашем случае функция, от которой берутся интегралы вдоль прямых, может принимать значения только «нуль» и «единица».
Другое отличие в том, что мы не пользуемся всем необходимым объемом информации, а лишь тем, который достаточен для определения геометрического
центра и оси минимальной инерции. В вопросах восстановления бинарных изображений по проекциям существует несколько интересных нерешенных задач. Допустим, например, что на изображении имеется непустая выпуклая область. Сколько проекций требуется для полного восстановления границы этой области? Далее, существуют ли некруглые объекты, обладающие тождественными с окружностью горизонтальными и вер-
тикальными проекциями?
95
2.3. Дискретные бинарные изображения
До сих пор мы рассматривали непрерывные бинарные изображения, определенные во всех точках плоскости. Должно быть очевидным, что при переходе к дискретным изображениям интегралы становятся суммами (рис. 3.8). Например, площадь вычисляется (в единицах площади элемента изображения) в виде суммы:
n m
A 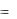 bij ,
bij ,
i 1 j 1
где btj — значение бинарного изображения в точке, находящейся в i-й строке и j-м

столбце. Здесь мы полагали, что поле изображения разбито на квадратную решетку с т столбцами и п строками.
Часто изображение просматривается строка за строкой в той же самой последовательности, в какой телевизионный луч бежит по экрану (если не учитывать того, что четные строки считываются вслед за нечетными). Как только считано значение очередного элемента изображения, проверяем равенство by = 1. Если оно выполняется, добавляем 1, i, j, i2, ij и j2 к накапливаемым значениям площади, первых моментов и вторых моментов. По окончании цикла сканирования с помощью этих значений легко найти площадь, положение и ориентацию.
96
Рис. 2.8. Дискретное бинарное изображение, состоящее из отдельных элементов, каждый из которых принимает значение «нуль» или «единица».
2.4. Кодирование с переменной длиной кодовой последовательности
Существует несколько способов кодирования, позволяющих еще больше сжать информацию о бинарных изображениях. Одним из широко распространенных является
кодирование с переменной длиной кодовой последовательности. Этот метод основан на том, что вдоль любой просматриваемой в данный момент строки обычно обнаруживаются длинные цепочки нулей и единиц. Поэтому вместо передачи отдельных битов информации мы можем посылать длины подобных цепочек. Код с переменной длиной для строки изображения есть просто [31, 32, 33, 34].
Для обозначения начала каждой строки нужно ввести специальный признак. Кроме того, принимается соглашение относительно того, с чего начинается строка (с нуля или единицы). Если строка начинается с противоположного символа, то первым символом
кода устанавливается нуль.
97
Условимся, что rik представляет собой k-ю цепочку в i-й строке и что первая цепочка в каждой строке есть цепочка нулей. (Таким образом, все четные цепочки будут соответствовать единицам на изображении.) Пусть mi — количество цепочек в i-й строке. Как использовать коды с переменной длиной для быстрого вычисления требуемых геометрических характеристик? Ясно, что площадь — просто сумма кодов цепочек, соответствующих единицам на изображении.
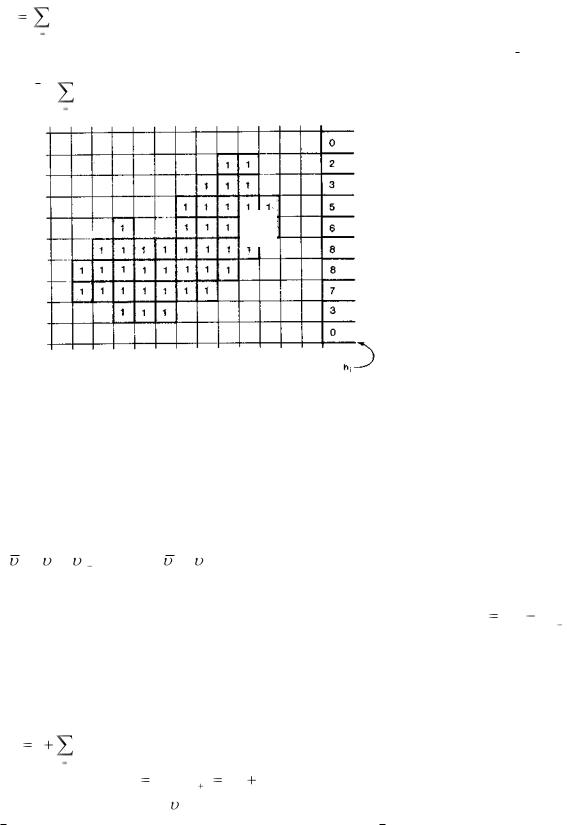
n mi / 2
Ari,2k
i1 k 1
Необходимо отметить, что суммирование распространяется лишь на четные цепочки.
Несколько труднее вычислить геометрический центр. Прежде всего следующим образом определяется горизонтальная проекция (рис. 2.9):
mi / 2
hi ri,2k k 1
Отсюда нетрудно найти вертикальное положение геометрического центра i :
n
Ai 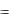 ihi
ihi
i 1
98
Рис. 2.9. Горизонтальная проекция, которая сопоставляет каждой строке количество элементов изображения, принимающих значение «единица»,
Нo как быть с вертикальной проекцией ύj? Вспомните: каждое значение этой проекции получается суммированием всех значений элементов изображения, расположенных в одном столбце. Поэтому непосредственное вычисление вертикальной проекции с помощью имеющихся в нашем распоряжении кодов затруднено.
Теперь рассмотрим первые разности значений вертикальной проекции
j  j
j  j 1 , причѐм 1
j 1 , причѐм 1 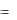 1 .
1 .
Их, очевидно, можно получить на основе информации, содержащейся не в самом
|
|
|
|
|
|
изображении, а в первых горизонтальных разностях изображения: bi, j bi, j bi, j |
1 |
||||
|
|
|
|
||
Первая разность bi, j имеет перед самим изображением bij то преимущество, |
что она |
||||
отлична от нуля только в начале каждой цепочки. Она равна +1 там, где значение
|
элемента изображения меняется с 0 на 1, и -1 там, где оно изменяется с 1 на 0 (рис. 2.10). |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
99 |
|
|
|||
|
Мы можем локализовать эти места, вычислив суммарные коды rik : |
||||||||||||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
ril |
|
|
|
|
|
|
|
|
|
||
rik |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
l |
1 |
|
|
|
|
|
|
|
|
|
|
|
или |
рекурсивно |
|
0 1 и |
|
|
|
, j 1 |
|
, j ri, j . После этого для получения первой разности |
||||||
ri |
ri |
ri |
|||||||||||||
вертикальной проекции |
|
j |
необходимо найти разность между числом суммарных кодов |
||||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
rik , равных j, с нечетным k и числом суммарных кодов rik , равных j, с четным k.
Из полученных первых разностей сама вертикальная проекция определяется простым суммированием

j
j |
l |
l 1
или рекурсивно ύ0=0 и ύj+1= ύj+ j 1 . Пример расчетов приведен на рис. 2.10. Зная
вертикальную проекцию, нетрудно найти горизонтальное положение j геометрического центра
|
|
m |
A j |
j j |
|
|
|
j 1 |
100
Рис. 2.10, Первые разности вертикальной проекции, вычисляемые с помощью проекции первых разностей для строк изображения.
Сама вертикальная проекция находится затем суммированием результата слева направо.
2.5.Бинарные изображения: топологические характеристики
Вэтой главе рассматриваются случаи, когда в поле зрения оказывается более одного объекта, а также разрабатываются более сложные методы восстановления информации по бинарным изображениям. Для этого необходимо тщательно определить, что мы понимаем под связностью двух элементов изображения. Мы изучим этот вопрос для различных способов разбиения плоскости изображения и разработаем средства, позволяющие помечать различные компоненты изображения при последовательном его просмотре.
Изображения содержат большой объем информации. Один из путей ее обработки за приемлемое время состоит в широком использовании распараллеливания процессов.
Существуют два изящных класса методов параллельной обработки бинарных
101
изображений (локальные методы и методы итеративной модификации), которые исследуются в данной главе. Для понимания того, какие величины можно вычислить в результате их применения, вводится свойство аддитивности.
Приведенные здесь методы могут найти применение в задачах визуальной инспекции, обнаружения и распознавания объектов.
2.5.1. Сложные объекты

Иногда в поле зрения попадает более одного объекта (рис. 4.1). В этом случае вычисление площади, геометрического центра и ориентации приведет к значениям, «усредненным» по всем компонентам бинарного изображения. Как правило, это не то, что требуется. Желательно как-то пометить отдельные компоненты изображения и вычислить значения площади, первых и вторых моментов для каждой компоненты в отдельности.
2.5.2. Разметка компонент Будем считать две точки изображения связанными, если существует путь между ними,
вдоль которого характеристическая функция постоянна. Так, на рис. 2.11 точка А связана с точкой В, но не связана с точкой С. Связная компонента бинарного изображения есть максимальное множество связанных точек, т. е. множество, состоящее из всех тех точек, между любыми двумя из которых существует связывающий их путь. На рисунке изображены четыре связные компоненты и четыре отверстия (кроме фона).
102
Рис. 2.11. Изображение, состоящее из нескольких областей, для каждой из которых необходимо проводить расчет положения и ориентации.
Элементы изображения необходимо пометить таким образом, чтобы принадлежащие одной области были отличимы от остальных. Для этого нам необходимо решить, какие точки принадлежат одной и той же области. На рисунке точка А считается связанной с точкой В, поскольку мы можем найти непрерывную кривую, целиком лежащую в затененной области и соединяющую указанные точки. Ясно, что точка А не связана с точкой С, так как в этом случае подобной кривой найти нельзя.
Один из способов разметки объектов на дискретном бинарном изображении состоит в выборе произвольной точки, в которой bij=1, и приписывании метки этой точке и ее соседям. На следующем шаге помечаются соседи этих соседей (кроме уже помеченных) и т. д. По завершении этой рекурсивной процедуры одна компонента будет полностью помечена, и процесс можно будет продолжить, выбрав новую начальную точку. Чтобы ее отыскать, достаточно каким-либо систематическим образом перемещаться по изображению до тех пор, пока не встретится первая еще непомеченная точка, в которой bij=1. Когда на этом этапе не останется ни одного такого элемента, все объекты изображения окажутся размеченными.
Ясно, что «фон» также можно разбить на связные компоненты, поскольку объекты могут иметь отверстия. Их можно пометить с помощью той же процедуры, но при этом
необходимо обращать внимание не на единицы, а на нули.
103
2.5.3. Связность Теперь пора аккуратно рассмотреть смысл термина сосед. Если мы имеем дело с
квадратным растром, то, по-видимому, соседями следует считать четыре элемента изображения, касающиеся сторон данного элемента. Но как быть с теми, которые касаются его в углах? Существуют две возможности:

-четырехсвязность: соседями считаются только элементы, примы кающие к сторонам;
-восьмисвязность: элементы, касающиеся в углах, также считаются соседями. Указанные возможности приведены на следующих диаграммах:
Оказывается, ни одна из этих схем не является полностью удовлетворительной. В этом можно убедиться, если вспомнить, что фон также можно разбить на несколько связных компонент. Здесь нам хотелось бы применить наши интуитивные представления о связности областей на непрерывном бинарном изображении. Так, например, простая замкнутая кривая должна разделять изображение на две связные области (рис. 2.12). Это так называемая теорема Жордана о кривой.
104
Рис. 2.12. Простая замкнутая кривая, разбивающая плоскость на две связные области.
Теперь рассмотрим простое изображение, содержащее четыре элемента со значением «единица», которые примыкают к центральному элементу со значением «нуль»:
Это - крест с выброшенным центром. Если принять соглашение о четырехсвязности, то на изображении окажутся четыре различные компоненты (O1, O2, О3 и O4):
Они, естественно, не образуют замкнутой кривой, хотя центральный элемент, относящийся к фону, и не связан с остальным фоном. Несмотря на отсутствие какой-либо замкнутой кривой, у нас образовались две фоновые области! Если принять соглашение о восьмисвязности, то, наоборот, четыре элемента растра станут образовывать замкнутую кривую, и в то же время центральный элемент окажется связанным с остальным фоном:
105

Итак, мы получили замкнутую кривую и только одну связную компоненту фона!
Одно из решений возникшей проблемы состоит в выборе четырехсвязности для объекта и восьмисвязности для фона (или наоборот). Подобная асимметрия в трактовке объекта и фона часто нежелательна и ее можно избежать путем введения другого типа асимметрии. Будем считать соседями четыре элемента изображения, примыкающие к данному по сторонам, а также два из четырех элементов, касающихся в углах:
Для обеспечения симметричности отношения связности два угловых элемента должны находиться на одной и той же диагонали: если элемент А — сосед элемента В, то элемент В должен быть соседом элемента А. В дальнейшем мы будем пользоваться первым из двух возможных вариантов, приведенных выше, считая соседями элементы в направлениях N, E, SE, S, W и NW ( ↑→ ↓← ) С помощью шестисвязности как объект, так и фон можно трактовать единообразно без каких-либо дальнейших неувязок. Для изображений на квадратном растре мы примем именно такое соглашение.
На гексагональном растре рассуждения проще. Все шесть элементов растра, касающиеся данного центрального элемента, являются соседями, так что неопределенности не возникает. Наши предыдущие действия можно рассматривать как
простой перекос квадратной решетки и превращение ее в гексагональную. Чтобы в этом
106
убедиться, зафиксируем произвольный элемент и сдвинем ряд, находящийся над ним, на половину ширины элемента вправо, а ряд, находящийся под ним,— на ту же величину влево:
Теперь выбранный элемент касается шести других, и они в точности такие, которые мы выбрали при определении шестисвязности.
2.5.4. Последовательный алгоритм разметки Теперь мы подготовлены к описанию алгоритма разметки, который лучше
приспособлен к последовательному сканированию изображения и не нуждается в рекурсивных вызовах. Допустим, что сканирование ведется строка за строкой, сверху вниз и слева направо (рис. 2.13).
Рис. 2.13. Решения, принимаемые при разметке.
