
Основы применения метода конечных элементов. Рукин Ю.Б
.pdf
Ю.Б. Рукин
ОСНОВЫ ПРИМЕНЕНИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
Учебное пособие
Воронеж 2003
3
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Воронежский государственный технический университет
Ю.Б. Рукин
ОСНОВЫ ПРИМЕНЕНИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
Утверждено Редакционно-издательским советом университета в качестве учебного пособия
Воронеж 2003
4

УДК 534 Рукин Ю.Б. Основы применения метода конечных эле-
ментов: Учеб. пособие Воронеж: Воронеж. гос. техн. ун-т, 2003..
114 с.
Рассмотрены основы дискретного моделирования статики и динамики линейно-упругих задач пространственных конструкций методом конечных элементов. Приведены необходимые для выполнения расчетов теоретические материалы. Затронуты вопросы автоматизированной подготовки исходных данных для проведения численного моделирования, приведены примеры моделирования.
Учебное пособие предназначено для студентов специальности 070200 при изучении дисциплины «Механика».
Учебное пособие подготовлено на магнитном носителе в текстовом редакторе MS WORD и содержится в файле
UPA5.doc.
Табл. 6. Ил. 56. Библиогр.: 11 назв.
Научный редактор д-р физ.-мат. наук В.Н.Нечаев
Рецензенты: кафедра «Строительных и дорожных машин» ВГАСУ (зав. кафедрой д-р техн. наук, проф. П.И.Никулин); канд. техн. наук Б.Б. Еськов
Рукин Ю.Б. 2003 Оформление: Воронежский государственный технический университет, 2003
5
ВВЕДЕНИЕ
Метод конечных элементов (МКЭ) в настоящее время является общепризнанным основным методом структурного анализа в целом ряде областей науки и техники. На основе этого метода разработано множество программных комплексов (NASTRAN, CAD-FEM, СПРИНТ, ЛИРА) для использования в аэрокосмической, автомобильной промышленности, в машиностроении и строительстве.
По своей сущности – это вариационный метод с кусочнополиномиальными пробными функциями, обладающий большой гибкостью и применимый к широкому классу уравнений в частных производных. МКЭ позволяет достаточно точно описать сложные криволинейные границы области определения решения, обеспечивает единственность приближенного решения во всех точках рассматриваемой области и обладает целым рядом достоинств в сравнении с другими методами.
Предлагаемое учебное пособие предназначено для студентов, аспирантов и инженеров, желающих овладеть практическими основами МКЭ, проверить свои знания при моделировании простейших задач строительной механики и сравнить полученные результаты с известными аналитическими решениями.
Детальное обсуждение основных этапов МКЭ сопровождается примерами, иллюстрирующими технику его применения.
Наиболее полно отражают теоретические основы и технологию применения МКЭ книги Зенкевича, Галлагера, Сегер-
линда /1,2,3/.
ОСНОВНАЯ ИДЕЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
Сущность МКЭ состоит в том, что любую непрерывную величину (перемещение, температуру или давление) можно
3
аппроксимировать дискретной моделью, которая формируется на множестве кусочно-непрерывных функций, определенных в конечном числе подобластей.
Кусочно-непрерывные функции определяются по значениям непрерывной величины в конечном числе точек исследуемой области. Непрерывная величина заранее неизвестна и требуется определить ее значение во внутренних точках области.
При построении дискретной модели непрерывной величины можно выделить следующие этапы.
1.В исследуемой области выделяется конечное число точек – узлов.
2.В каждой узловой точке должно быть определено значение непрерывной величины.
3.Область определения непрерывной величины расчленяется на конечное число подобластей (элементов). Элементы имеют общие узлы и аппроксимируют форму области.
4.В каждом элементе непрерывная величина аппроксимируется полиномом, который определяется с помощью узловых значений этой величины. Полиномы подбираются таким образом, чтобы сохранялась непрерывность величины вдоль границ элемента.
Вдальнейшем рассматривается метод конечных в перемещениях и в качестве непрерывной величины выступает функция перемещений. Перемещение внутри каждого элемента однозначно определяется через перемещения узловых точек.
Функции перемещений однозначно определяют деформации внутри элемента. Эти деформации позволяют определить напряжения внутри элемента и на его границах.
1.Формируется система узловых сил, уравновешивающих напряжения на границе и распределенные нагрузки.
2.Строятся матрицы жесткости конечных элементов, на основании которых формируется матрица жесткости всей совокупности элементов.
3.Учитываются наложенные внешние связи и строится система разрешающих уравнений МКЭ в перемещениях. По-
4
лученные в результате решения этой системы узловые перемещения полностью определяют напряженно-деформи- рованное состояние исследуемой конструкции.
ПРЕИМУЩЕСТВА И НЕДОСТАТКИ МКЭ
Наиболее важными преимуществами являются:
1.Свойства материалов смежных элементов могут быть различными, что позволяет применять метод к телам, составленным из нескольких материалов.
2.Область с криволинейной границей может быть аппроксимирована элементами, имеющими прямолинейные стороны.
3.Размеры элементов могут быть переменными, что позволяет измельчать сетку разбиения в зонах предполагаемой концентрации напряжений.
4.Не представляет труда рассмотрение граничных условий с разрывной поверхностной нагрузкой.
5.Многие этапы реализации МКЭ для различных классов задач являются одинаковыми.
Недостатками МКЭ являются необходимость составления вычислительных программ и применение вычислительной техники. Вычисления, которые требуется проводить при использовании МКЭ, слишком громоздки для ручного счета даже в случае решения очень простых задач.
ДИСКРЕТИЗАЦИЯ ОБЛАСТИ
Разбиение на элементы области, в которой строится решение задачи, является важным этапом, определяющим эффективность реализации МКЭ. Успех дискретизации области зависит от знания физики исследуемого явления, общих особенностей поведения искомого решения, а также от учета влияния типа сетки на эффективность численного решения дискретной задачи.
5
Дискретизация области включает задание числа, размеров и формы элементов, которые используются для построения дискретной модели исследуемого объекта. Для обеспечения требуемой точности искомого решения элементы должны быть достаточно малыми, чтобы аппроксимируемые поля достаточно хорошо описывались полиномами. Однако малость элементов приводит к дискретным задачам больших размерностей, что увеличивает объем вычислительной работы.
На основе общих соображений необходимо измельчать сетку лишь в тех подобластях, где искомое решение имеет большие значения градиентов и использовать достаточно крупные элементы там, где решение почти постоянно.
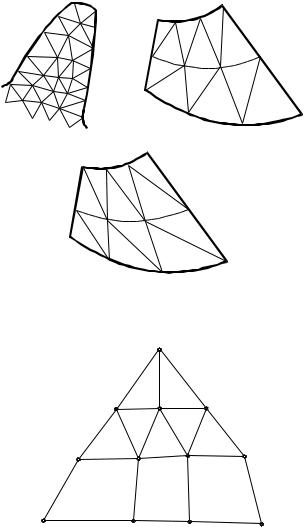
При разбиении двумерной области на элементы тело делится на треугольные и четырехугольные подобласти. Границы между подобластями должны проходить там, где изменяются геометрия, приложенная нагрузка или свойства материала. При дискретизации подкрепленных конструкций необходимо, чтобы подкрепляющее ребро проходило вдоль кромки элемента. На рис. 1 представлены примеры разбиения исследуемых областей на треугольные элементы.
При разбиении области на треугольные элементы, вначале делят ее на четырехугольные подобласти, которые затем делят вдоль короткой диагонали на два треугольных элемента (рис. 1, б). Нежелательным разбиением является показанное на рис. 1, в, так как элементы, близкие по форме к равностороннему треугольнику, дают более точные результаты, чем длинные узкие треугольники.
Четырехугольные элементы могут быть смежными с треугольными, но необходимо, чтобы число узлов на их общей границе было одинаковым и относительное положение узлов должно совпадать. Это необходимо для обеспечения непрерывности рассматриваемых величин вдоль общей границы элементов (рис. 2).
6
а) |
б) |
в)
Рис. 1. Примеры триангуляции областей
Рис. 2. Пример сетки из треугольных и четырехугольных элементов
При необходимости сгущения сетки треугольных элементов можно воспользоваться способом, изображенным на рис. 3.
7
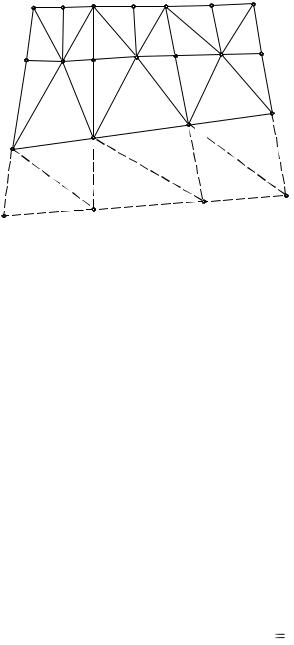
Рис. 3. Пример переходной зоны сгущения сетки триангуляции
Вторым этапом дискретизации является нумерация узлов и элементов. При хорошей нумерации узлов эффективность вычислений повышается. Использование МКЭ приводит к системе линейных алгебраических уравнений, большое число коэффициентов которой равно нулю. Исследование матрицы коэффициентов показывает, что все ненулевые коэффициенты сосредоточены вблизи диагонали, т.е. матрица имеет ленточный вид. Расстояние между главной диагональю и параллельными ей линиями, отделяющими зоны нулевых коэффициентов от ненулевых, называется полушириной ленты матрицы. Все нулевые коэффициенты вне полосы не должны храниться в машинной памяти. Уменьшение ширины ленты матрицы приводит к сокращению размеров требуемой машинной памяти и, в итоге, к сокращению времени вычислений.
На рис. 4, а изображена область из треугольных конечных элементов, аппроксимирующая крыло малого удлинения.
Матрица жесткости ансамбля конечных элементов имеет ленточную структуру (рис. 4,б), где кружками обозначены ненулевые коэффициенты, возникающие из-за связи элементов
(если узлы i, j не принадлежат элементу e, то |
K e |
0 ). В этом |
|
ij |
|
8 |
|
|
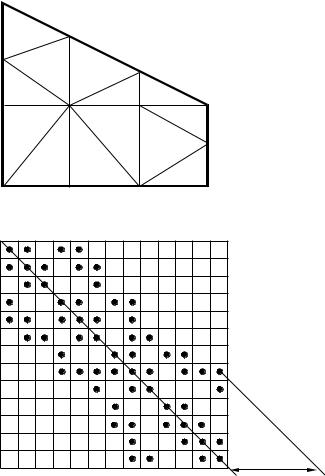
случае процедура решения должна использовать ленточность структуры матрицы жесткости, а узлы нумеруются таким образом, чтобы обеспечить минимум ширины ленты: это значительно увеличивает скорость вычислительного процесса.
10
|
|
|
7 |
|
|
|
|
11 |
|
|
|
|
|
4 |
|
12 |
|
8 |
|
|
|
5 |
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
13 |
|
|
9 |
а) |
|
6 |
3 |
|
|
|
|
|
|
|
|
1 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 10 11 12 13 |
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
B |
б)
Рис. 4. Пример сетки (а) и схемы размещения ненулевых коэффициентов глобальной матрицы жесткости (б)
9
