
2418
.pdf
Таблица 5
Низшие частоты собственных колебаний защемленной конической оболочки
i , Гц |
1 |
2 |
3 |
4 |
5 |
6 |
|
Трапециевидный |
1337 |
1337 |
1645 |
1645 |
1774 |
1774 |
|
элемент |
|||||||
|
|
|
|
|
|
||
Pro/MECHANICA |
1324 |
1324 |
1786 |
1786 |
1825 |
1826 |
|
Погрешность, % |
1 |
1 |
8 |
8 |
3 |
3 |
На рис. 49 показаны некоторые характерные формы собственных колебаний низших частот.
Оболочка в виде сектора кругового тора с углом раствора 45 имеет радиус поперечного сечения 7 10–2 м, радиус образующей 21 10–2 м и толщину 0.1 10–2 м. Материал оболочки имеет следующие характеристики: E = 2.1 1011 Н/м2, = 0.3, = 7.85 103 кг/м3. Одно крайнее поперечное сечение защемлено, другое – свободно. В таблице 10 представлены результаты чис-
имеет радиус поперечного сечения 7 10–2 м, радиус образующей 21 10–2 м и толщину 0.1 10–2 м. Материал оболочки имеет следующие характеристики: E = 2.1 1011 Н/м2, = 0.3, = 7.85 103 кг/м3. Одно крайнее поперечное сечение защемлено, другое – свободно. В таблице 10 представлены результаты чис-
ленного анализа.
Таблица 6
Низшие частоты собственных колебаний оболочки в виде сектора кругового тора, защемленной по одному крайнему поперечному сечению
i, |
Трапециевидный |
Pro/ |
Погрешность, |
Гц |
элемент |
MECHANICA |
% |
1 |
569 |
558 |
2 |
|
|
|
|
2 |
569 |
566 |
0.5 |
|
|
|
|
3 |
952 |
1050 |
9 |
|
|
|
|
На рис. 50 изображены формы собственных колебаний оболочки.
70

1
3
5
Рис. 52. Низшие собственные формы конической оболочки
71

1
3
5
Рис. 53. Низшие собственные формы сектора торообразной оболочки
72
Разработанный трапециевидный конечный элемент обладает следующими преимуществами:
-линии конечноэлементной сетки совпадают с линиями главных кривизн оболочек со срединными поверхностями вращения, обеспечивая тем самым лучшую аппроксимацию полей напряжений и перемещений;
-аналитические выражения для компонентов матриц инертности повышают точность и быстроту их вычисления, по сравнению с численным интегрированием;
-обеспечивает возможность моделирования оболочек с произвольным изменением толщин элементов вдоль меридианов и параллелей срединной поверхности вращения;
-алгоритм генерации конечноэлементной сетки для оболочек со срединными поверхностями вращения легко поддается автоматизации;
-достаточно высокая точность определения частот и форм собственных колебаний, даже при весьма грубой конечноэлементной сетке.
Моделирование массивных конструкций
При проектировании различных механизмов и машин, инженерных сооружений часто возникает необходимость оценить напряженно-деформированное состояние массивных частей этих конструкций. Достаточно полную информацию о распределении напряжений и перемещений в таких телах можно получить, используя численные методы. Метод конечных элементов позволяет выявить особенности распределения силовых потоков и деформаций в деталях, имеющих сложные конфигурации, препятствующие применению аналитических методов.
При построении модели используется конечный элемент в виде пирамиды с треугольным основанием. В качестве узлов i, j, k, m приняты его вершины (рис.54).
Перемещения вдоль осей x,y,z распределяются по линейному закону:
73

u( x, y,z ) v( x, y,z ) w( x, y,z )
 1
1  2 x
2 x  3 y
3 y  4 z
4 z
5 |
6 x |
7 y |
8 z |
(1) |
9  10 x
10 x  11 y
11 y  12 z
12 z
|
|
m |
|
z |
i |
|
|
|
|
0 |
k |
|
|
|
x |
|
y |
|
|
j |
Рис. 54. Конечный элемент в форме тетраэдра
иего узловые степени свободы
Ваппроксимирующем полиноме 12 независимых коэффициентов, соответствующих трем степеням свободы в каждом узле.
Для построения матрицы жесткости необходимо аппроксимацию полиномами (1) получить в явном виде, связав коэф-
фициенты |
i |
полиномов со степенями свободы. Считаем, что |
|
|
перемещения u вдоль оси x зависят только от перемещений u1 , u2 , u3 , u4 ; перемещения вдоль оси y зависят только от
v1,v2 ,v3 ,v4 и т.д. (локальные номера узлов 1-4 соответствуют
глобальным номерам узлов i, j, k, m). Если в полиномы (1) подставить координаты узла i, то u = ui и т.д., т.е:
u1 |
1x1 y1 z1 |
1 |
|
|
|
||
u2 |
1x2 y2 z2 |
2 |
. |
|
|
||
u3 |
|
|
|
1x3 y3 z3 |
3 |
|
|
|
|
|
|
u4 |
1x4 y4 z4 |
4 |
|
|
|
|
74

Из этого выражения можно найти коэффициенты аппроксимаций:
1 |
a1a2 a3a4 |
u1 |
2 |
b1b2b3b4 |
u2 |
3 |
c1c2c3c4 |
u3 |
4 |
d1d2 d3d4 |
u4 |
Аппроксимация перемещений u(x,y,z) вдоль оси x в явном виде примет вид:
u( x, y,z ) ( a1 |
b1 x c1 y d1 z )u1 |
( a2 b2 x c2 y d2 z )u2 |
||||||||||
( a3 |
b3 x c3 y d3 z )u3 |
( a4 |
b4 x c4 y d4 z )u4 , |
|||||||||
где: |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 y2 z2 |
|
|
|
1y2 z2 |
|
|
|
1x2 z2 |
|
||
|
|
|
|
|
|
|
|
|||||
a1 1/ |
x3 y3 z3 |
; b1 |
1/ |
1y3 z3 |
; |
c1 |
1x3 z3 |
; |
||||
|
x4 y4 z4 |
|
|
|
1y4 z4 |
|
|
|
1x4 z4 |
|
||
|
|
|
|
1x2 y2 |
|
|
|
|
||||
|
|
|
|
|
|
1x1 y1 z1 |
|
|||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
1x2 y2 z2 |
|
|
|
|||
d1 |
1/ |
1x3 y3 |
; |
|
|
|||||||
|
1x3 y3 z3 |
|
|
|
||||||||
|
|
|
|
1x4 y4 |
|
|
|
|||||
|
|
|
|
|
|
1x4 y4 z4 |
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
Значения a2 ,b2 ,c2 , d2 и т.д. определяются с помощью кру-
говой перестановки узловых индексов. Выражения для v(x,y,z) и w(x,y,z) полностью аналогичны выражению для u(x,y,z).
|
Используя |
основные соотношения |
теории упругости |
|||
|
E ; |
D u , можно вычислить компоненты матрицы |
||||
жесткости, например, для коэффициента |
|
|||||
|
|
k12 |
T |
V d |
c1b1 |
, |
|
|
u |
||||
|
|
|
1 |
1 |
|
|
где |
/ 6 – объем тетраэдра. |
|
|
|
||
|
Перед проведением вычислений создается расчетная мо- |
|||||
дель, |
отбрасыванием |
несущественных деталей исследуемой |
||||
75

конструкции и назначением для каждого элемента конструкции соответствующих характеристик. На основе этой модели формируются массивы координат узлов, расположенных в вершинах объемных элементов и матрица связей, в которую включаются номера узлов, принадлежащих данному конечному элементу. Задаются узловые нагрузки и граничные условия. В качестве примера моделируется защемленный одним своим крайним поперечным сечением брус и нагруженный двумя силами в плоскости свободного сечения (рис.55).
0,1
x
z
|
|
|
|
Px = 100 H |
41 44 |
|
Py = 100 H |
||
42 |
|
43 |
|
|
|
|
|
||
38 |
|
40 |
|
|
|
|
|
|
|
|
|
39 |
|
|
|
|
|
|
0,25 X 10 = 2,5 м |
10 |
11 |
12 |
|
|
6 |
7 |
8 |
|
|
|
,1 |
|||
|
|
|
||
2 |
|
4 |
0 |
|
|
|
|
||
|
|
|
|
|
|
3 |
|
|
y |
Рис. 55. Пример расчета
В данном примере для упрощения подготовки данных вначале исследуемая конструкция разбивается на прямоугольные параллелепипеды, а затем каждый такой объемный эле-
76

мент программно представляется в виде совокупности тетраэдральных конечных элемента (рис.56).
6

 1
1
2  4
4
x
6
 7 2
7 2 4
4
5
6 |
|
8 |
|
|
|
|
|
|
|
||
|
5 |
4 |
|
|
|
6 |
|
|
5 |
||
|
|
||||
|
|
|
|||
|
|
8 |
6 |
|
|
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|||
|
|
|
|||
|
1 |
||||
|
4 |
||||
z |
4 |
|
 5
5
6 


 8 1
8 1
 7
7

2 




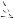
 4 y
4 y
|
3 |
|
|
|
6 |
|
8 |
6 |
8 |
|
7 |
|||
|
|
|
|
|
2 |
|
4 |
|
7 |
|
|
|
4 |
|
|
|
|
|
|
|
3 |
|
|
|
|
7 |
|
|
|
2 |
4 |
|
|
|
3 |
Рис. 56. Схема разбиения четырехгранной призмы на тетраэдры
Для каждого тетраэдра записывается матрица связей и формируется массив узловых координат. При формировании матрицы связей принят следующий порядок обхода узлов: если смотреть со стороны последнего узла, то остальные узлы нумеруются против хода часовой стрелки. При формировании
77

конечно-элементной модели необходимо стремиться к такой форме конечных элементов, чтобы длины его ребер не отличались друг от друга более, чем в пять раз. Описанный процесс формирования исходных данных производится на предварительном этапе, который выполняет программа brus_d.f. На первом шаге по сформированным матрицам связей и координат узлов вычисляются матрицы жесткости и записываются в отдельный файл для дальнейших расчетов. Этот шаг выполняется программой s1.f . Для выполнения первого шага необходимо задать в файле DT1 количество элементов и узлов, механические характеристики материала элементов. На следующем шаге формируется глобальная матрица жесткости расчетной модели с учетом заданных граничных условий (программа S2.f). Граничные условия, нагрузки и размер формируемой фазы системы уравнений вводятся в файле DT2. Решение полученной системы линейных алгебраических уравнений проводится программой S3.f. Полученный массив узловых перемещений, позволяет затем вычислить напряжения в каждом конечном элементе (программа S4.f). На основании полученной информации можно сделать вывод о напряженно-деформи- рованном состоянии исследуемой конструкции и, при недостаточной прочности, изменить геометрические размеры или механические характеристики материала, проведя описанный расчет вновь. В рассмотренной модели последний узел нагружен двумя силами по 100 Н, узлы 1, 2,3, 4 лишены всех степеней свободы. Материал элементов модели имеет следующие
механические характеристики: E 2 1011 Н / м2 , |
0.3 . |
В приложении 4 представлены тексты программ этапов моделирования массивных конструкций.
Для рассматриваемого примера необходимые данные задаются в файлах:
DT0
44,132,10,60,4,2
0.,0.,0.
0.1,0.,0.
78
0.1,0.1,0.
0.,0.1,0.
0.,0.,0.25
0.1,0.,0.25
0.1,0.1,0.25
0.,0.1,0.25
0.,0.,0.5
0.1,0.,0.5
0.1,0.1,0.5
0.,0.1,0.5
0.,0.,0.75
0.1,0.,0.75
0.1,0.1,0.75
0.,0.1,0.75
0.,0.,1.00
0.1,0.,1.00
0.1,0.1,1.00
0.,0.1,1.00
0.,0.,1.25
0.1,0.,1.25
0.1,0.1,1.25
0.,0.1,1.25
0.,0.,1.50
0.1,0.,1.50
0.1,0.1,1.50
0.,0.1,1.50
0.,0.,1.75
0.1,0.,1.75
0.1,0.1,1.75
0.,0.1,1.75
0.,0.,2.00
0.1,0.,2.00
0.1,0.1,2.00
0.,0.1,2.00
0.,0.,2.25
0.1,0.,2.25
79
