
2418
.pdf
m |
2.777778 |
10 3 |
lt / a2 ( 30a2lk |
80a3 |
k 3l3 6al2 k 2 ); |
|||
11 |
|
|
|
|
|
|
|
|
m |
2.777778 |
10 3 |
lt / a2 ( |
6al2 k 2 |
k 3l3 |
40a3 ); |
|
|
12 |
|
|
|
|
|
|
|
|
m |
2.777778 |
10 3 |
lt / ab( |
30a2b |
2k 3l3 |
15a2lk |
9al2 k 2 |
|
13 |
|
|
|
|
|
|
|
|
|
10a3 |
15albk ); |
|
|
|
|
|
|
m |
2.777778 |
10 3 |
lt / ab( 9al2 k 2 |
15a2lk |
30a2b |
15albk |
||
14 |
|
|
|
|
|
|
|
|
|
10a3 |
2k 3l 3 ). |
|
|
|
|
|
|
Выражения для первых трех коэффициентов матрицы инертности изгибного состояния
|
|
( f1 |
3.3068 |
10 6 |
t, f 2 |
6.6137 |
10 6 |
t ): |
||||
m |
f l / a6 (150al 2b4 k 2 |
15l 7 k 7 |
81120a7 |
1535l 3a4 k 3 |
23985la 6 k |
|||||||
11 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
240l 4 a3k 4 |
35b4 k 3l 3 |
1656b2 a5 |
300ab2l 4 k 4 |
225lb4 a2 k |
|||||||
|
495l 5 a2 k 5 |
42l 5b2 k 5 |
390l 2 a5 k 2 |
120b4 a3 |
600l 3b2 a2 k 3 |
|||||||
|
120l 2b2 a3k |
1710la 4b2 k |
150al6 k 6 ); |
|
|
|
|
|||||
m |
f |
l 2 / a4 ( 5442a5 |
75l 2 k 2b2 a |
135a2lb2 k |
15l 3k 3b2 |
165l 2 k 2 a3 |
||||||
12 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
160l 3k 3a2 |
2385a4lk |
9l 5 k 5 |
75l 4 k 4 a |
90b2 a3 ); |
|
||||||
m |
f l / a5 (18792a7 645l 3a4 k 3 |
810l 4 a3k 4 |
150al6 k 6 |
450l 2b2 a3k 2 |
||||||||
13 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
225lb4 a2 k |
150al 2b4 k 2 |
15l 7 k 7 |
120b4 a3 |
42l 5b2 k 5 |
1935la 6 k |
||||||
|
3216b2 a5 |
35b4 k 3l 3 |
1710la 4b2 k |
710l 3b2 a2 k 3 4380l 2 a5 k 2 |
||||||||
|
300al 4b2 k 4 |
561l 5 a2 k 5 ). |
|
|
|
|
|
|
|
|||
Рассматривается наиболее важный и широко распространенный случай динамического анализа – исследование собственных колебаний конструкций без диссипации энергии.
Исследование частот и форм собственных колебаний упругих систем осуществлено на основе матричного уравнения [A]{x} 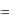 [B]{x}, соответствующего обобщенной проблеме соб-
[B]{x}, соответствующего обобщенной проблеме соб-
ственных значений. Метод конечных элементов, примененный к задачам такого типа, приводит согласно [7] к уравнению
[K]{x}  [M ]{x} ,
[M ]{x} ,
60

где: [K] – матрица жесткости системы; [M] – матрица инертности;
 – собственные значения.
– собственные значения.
Определение частот и форм выполнено в рамках неполной проблемы собственных значений [7]. Для ее решения выбран наиболее простой метод обратной итерации.
Тестирование матрицы инертности трапециевидного конечного элемента проведено на ряде аналитических задач и численных примеров, выполненных другими авторами.
1. Собственные частоты колебаний прямоугольной упругой пластинки, защемленной по одной короткой стороне и свободной по трем другим (рис. 39).
|
|
1 |
|
a |
z |
|
|
|
y |
2 |
4 |
|
||
|
|
6 |
|
|
t |
b
3 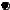 5
5
x
Рис. 39. Сетка элементов защемленной прямоугольной пластинки:
(a=2.54 10-2 м, b=2a, t=0.25 10-2 м, E=2.02 1011 H/м2, = 0.3, = 7798 кг/м3)
В таблице 1 приведены значения первых трех частот, найденные различными способами. При исследованиях использованы результаты решения рассматриваемой проблемы в среде программного продукта Pro/MECHANICA [8].
61

|
|
|
|
Таблица 1 |
|
|
Низшие частоты собственных колебаний |
||||
|
прямоугольной пластинки |
|
|||
|
|
|
|
|
|
i, |
Аналитиче- |
МКЭ, 4 |
МКЭ, 2 |
|
|
ское решение |
треуг. |
трапец. |
Pro/MECH. |
||
Гц |
|||||
[9] |
элемента |
элемента |
|
||
|
|
||||
1 |
815 |
805 |
815 |
813 |
|
|
|
|
|
||
2 |
3534 |
3632 |
3558 |
3373 |
|
|
|
|
|
||
3 |
5121 |
5025 |
5121 |
5012 |
|
|
|
|
|
||
|
|
|
|
|
|
2. Собственные частоты колебаний косоугольной упругой пластинки (рис. 40), защемленной вдоль двух смежных сторон.
|
a |
z |
x |
|
y
Рис. 40. Конечноэлементная сетка косоугольной пластинки:
(a=6 10-2 м, t=0.25 10-2 м, =26 , E=2.02 1011 H/м2, = 0.3, = 7798 кг/м3)
С целью простейшего разбиения указанной пластинки использована конечноэлементная сетка, образованная границами шести трапециевидных элементов. Результаты представлены в таблице 2.
62

Таблица 2
Низшие частоты собственных колебаний косоугольной пластинки
i , Гц |
1 |
2 |
3 |
4 |
5 |
6 |
|
Трапециевид- |
1004 |
3641 |
4554 |
7155 |
10432 |
12069 |
|
ный элемент |
|||||||
|
|
|
|
|
|
||
Pro/ |
1024 |
3820 |
4190 |
7467 |
10013 |
11196 |
|
MECHANICA |
|||||||
|
|
|
|
|
|
||
Погрешность, |
2 |
5 |
8 |
4 |
4 |
8 |
|
% |
|||||||
|
|
|
|
|
|
3. Найдены собственные частоты и формы кольцевой пластинки (рис. 41), защемленной вдоль стороны большего радиуса.
t=0,25 .10-2
M
r=1 .10 |
-2 |
R=3 .10 |
-2 |
M |
M |
y |
z |
x |
|
|
Рис. 41. Конечноэлементная сетка защемленной кольцевой пластинки
Низшие частоты собственных колебаний, вычисленные аналитически [9] и полученные при конечноэлементном моделировании представлены в таблице 3.
63

|
|
|
|
Таблица 3 |
|
|
Низшие частоты собственных колебаний |
||||
|
защемленной кольцевой пластинки |
||||
|
|
|
|
|
|
i, |
Аналити- |
Трапецие- |
Треуголь- |
Pro/ |
|
ческое |
видный |
ный эле- |
|||
Гц |
MECHANICA |
||||
решение |
элемент |
мент |
|||
|
|
||||
|
|
|
|
|
|
1 |
8126 |
7998 |
8479 |
8011 |
|
2 |
14071 |
12644 |
13908 |
12453 |
|
|
|
|
|
||
3 |
— |
13053 |
14402 |
12453 |
|
|
|
|
|
|
|
4 |
— |
20922 |
21619 |
20630 |
|
|
|
|
|
||
Собственные формы, соответствующие найденным частотам показаны на рис. 42–45.
Рис. 42. Низшая собственная форма |
|
защемленной кольцевой пластинки для |
1 |
64

Рис. 43. Низшая собственная форма защемленной кольцевой пластинки для
Рис. 44. Низшая собственная форма защемленной кольцевой пластинки для
Рис. 45. Низшая собственная форма защемленной кольцевой пластинки для
65
2
3
4

4. Тестирование матрицы инертности трапециевидного элемента проведено также при определении собственных частот цилиндрической оболочки, защемленной с двух сторон (рис. 46). Пример взят из [10], размеры указаны на рисунке.
t=0,0525 |
R 1,0 |
3,0
Рис. 46. Защемленная цилиндрическая оболочка
(размеры в м, =1 кг/м3, E = 104 Па, = 0.2)
Решение сравнивалось с результатами исследований при помощи комплекса Pro-MECHANICA, а также конечноэлементного моделирования пластинчатыми элементами треугольной формы и элементом CAU2W30 (Табл. 4).
Таблица 4
Минимальная частота собственных колебаний защемленной цилиндрической оболочки
Низшая |
Трапецие- |
Треуголь- |
Элемент |
Pro/ |
|
видный |
ный эле- |
||||
частота |
CAU2W30 |
MECHANICA |
|||
элемент |
мент |
||||
|
|
|
|||
i, Гц |
3.36 |
3.61 |
3.50 |
3.47 |
|
|
|
|
|
|
Расхождение результатов при определении низшей собственной частоты не превышает 5%.
66

5. Поведение цилиндрической оболочки с вырезом при собственных колебаниях рассмотрено на примере, описанном в [11]. На рис. 47 изображена исследуемая оболочка и приведены ее параметры.
t=0,00362
0,06 |
30o |
|
R 0,175
0,22 0,44
Рис. 47. Цилиндрическая оболочка с вырезом
(размеры в м, =7800 кг/м3, E = 2.1 1011 Па, = 0.3)
Собственные частоты, полученные при конечноэлементном моделировании с использованием тестируемого элемента отличаются от соответствующих значений представленных в [11] не более, чем на 5%. Некоторые формы собственных колебаний показаны на рис. 48–51.
6. В качестве примеров использования трапециевидного конечного элемента рассмотрены задачи определения собственных частот и форм конической оболочки и оболочки в виде сектора тора. Оболочка толщиной 0.1 10–2 м в виде прямого усеченного конуса длиной 15 10–2 м защемлена по стороне, имеющий радиус. 7 10–2 м; сторона конуса меньшего радиуса 4 10–2 м – свободна. В таблице 5 приведены собственные частоты, определенные численно разными авторами.
67

Рис. 48. Низшая собственная форма цилиндрической оболочки с вырезом для
Рис. 49. Низшая собственная форма цилиндрической оболочки с вырезом для
68
1
2

Рис. 50. Низшая собственная форма цилиндрической оболочки с вырезом для
Рис. 51. Низшая собственная форма цилиндрической оболочки с вырезом для
69
3
4
