2418

ния которой в файле DTE2 вводятся граничные условия: номера закрепленных узлов и условия закрепления (соответственно массивы NBC и NFIX).

Программа s3_3.f реализует процедуру формирования глобальной матрицы инертности модели конструкции (для введения граничных условий используется уже упомянутый файл DTE2).

Пофазное решение неполной проблемы собственных значений производится в программе s4_3.f. В ходе решения выводятся частоты собственных колебаний и соответствующие им собственные векторы.

ПРИМЕР ИСПОЛЬЗОВАНИЯ ПРОГРАММЫ ОПРЕДЕЛЕНИЯ СОБСТВЕННЫХ ЧАСТОТ ТОНКОСТЕННЫХ КОНСТРУКЦИЙ

На рис. 30 изображена исследуемая пластинка толщиной 0.0025 м, с защемлением вдоль одной из коротких сторон. У материала пластинки имеются следующие характеристики: модуль Юнга 2.02 1011 Н/м2, коэффициент Пуассона 0.3, плотность 7.798 103 кг/м3.

Для проведения вычислений на первом шаге необходимо подготовить файл DTE, который содержит следующую информацию:

40

2.02e11 7.798e03 0.3 0.0025

1 0. 0. 0.

20. 0.0254 0.

30.0254 0. 0.

40.0254 0.0254 0.

50.0508 0. 0.

60.0508 0.0254 0.

11 3 2

22 3 4

33 6 4

43 5 6

Впрограмме вычисления матриц жесткости и инертности конечных элементов необходимо задать параметры:

parameter(nstm=18, np=6, ne=4, ncn=3, nszf=36, ndf=3, ndfg=6),

где nstm – число узловых степеней свободы треугольного пластинчатого конечного элемента, np – число узлов, ne – число конечных элементов , nszf – число степеней свободы ансамбля конечных элементов, ndf – размерность пространства, ndfg – число степеней свободы узла в глобальной системе отсчета.

Результат выполнения программы помещен в файл

RES1_3:

em= 2.0200001E+11 ro=7798.165 thin=2.4999999E-03 pr= 0.3000000

В программах формирования глобальных матриц жесткости и инертности задаются параметры:

parameter(ndfg=6,ncnm=3,nstm=18,np=6,ne=4,ndf=6,nb=2,nband=24, imax=36,nszf=36,ncn=3),

где, кроме представленных ранее, введены: ncnm – максимальное число узлов элемента (в данном примере используются только треугольные конечные элементы, поэтому число узлов в каждом элементе ncn совпадает с ncnm), на данном этапе ndf

41

обозначает число узловых степеней свободы в локальной системе координат, nb – число граничных узлов, nband – полуширина ленты глобальной матрицы жесткости, imax – число уравнений, обрабатываемых в одной фазе.

Результаты выполнения программ второго и третьего шагов представлены в файлах RES2_3 и RES3_3:

1111111

2111111 nszf=36 nszf1=20

nband=24 imax=36 ik=20 knul=16,

где nszf1 – число уравнений с учетом граничных закреплений, ik – число уравнений последней фазы (в нашем примере одна фаза), knul – число исключаемых уравнений в соответствии с граничными условиями. Эти данные в качестве параметров вводятся на заключительном этапе:

parameter(neig=6,nit=200,test=1.e- 05,nszf1=20,nszf=36,imx=20,nband=24,knul=16),

где neig – число определяемых собственных частот, nit – предельное число итераций при определении каждой собственной частоты, test – точность вычисления собственного вектора.

Файл RES4_3 включает массивы узловых перемещений для каждой собственной частоты:

EIGF n= 20 neig=6 nit=200 test=9.9999997E-06

перемещения узлов, it= 5 nnnk= 36

1 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00

2 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00

30.473E-14 0.130E-13 -0.671E-02 -0.482E-01 0.445E+00 0.000E+00

4-0.531E-14 0.146E-13 -0.639E-02 0.418E-01 0.434E+00 0.000E+00

50.608E-14 0.296E-13 -0.197E-01 -0.193E-01 0.535E+00 0.000E+00

6-0.718E-14 0.294E-13 -0.195E-01 0.553E-01 0.565E+00 0.000E+00 omm= 2.5592680E+07 om= 5058.921

42

2 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00

30.469E-15 0.129E-14 -0.492E-02 0.369E+00 0.165E+00 0.000E+00

4-0.527E-15 0.145E-14 0.385E-02 0.325E+00 -0.196E+00 0.000E+00

50.603E-15 0.294E-14 -0.714E-02 0.609E+00 -0.696E-03 0.000E+00

6-0.713E-15 0.292E-14 0.827E-02 0.549E+00 -0.145E+00 0.000E+00 omm= 5.2099952E+08 om= 22825.41

3-0.175E-07 -0.480E-07 -0.429E-02 -0.169E+00 -0.627E-01 0.000E+00

40.197E-07 -0.542E-07 -0.587E-02 0.946E-01 -0.243E-01 0.000E+00

5-0.225E-07 -0.110E-06 0.835E-02 0.508E-01 -0.681E+00 0.000E+00

60.266E-07 -0.109E-06 0.520E-02 -0.307E+00 -0.630E+00 0.000E+00 omm= 9.9697536E+08 om= 31574.92

3 -0.145E-01 -0.398E-01 0.407E-02 -0.300E+00 0.270E+00 0.000E+00

40.163E-01 -0.450E-01 -0.541E-02 -0.268E+00 -0.126E+00 0.000E+00

5-0.187E-01 -0.911E-01 -0.679E-02 0.392E+00 0.312E+00 0.000E+00

60.221E-01 -0.904E-01 0.725E-02 0.509E+00 -0.466E+00 0.000E+00 omm= 5.2051748E+09 om= 72146.90

30.310E-04 0.851E-04 0.409E-02 -0.305E+00 0.272E+00 0.000E+00

4-0.349E-04 0.960E-04 -0.551E-02 -0.270E+00 -0.127E+00 0.000E+00

50.399E-04 0.194E-03 -0.682E-02 0.397E+00 0.312E+00 0.000E+00

6-0.472E-04 0.193E-03 0.736E-02 0.514E+00 -0.475E+00 0.000E+00 omm= 5.4474230E+09 om= 73806.66

3-0.415E-06 -0.201E-06 0.116E-02 -0.271E+00 -0.473E+00 0.000E+00

4-0.333E-06 -0.123E-06 -0.296E-03 0.120E+00 -0.215E+00 0.000E+00

5-0.541E-06 -0.251E-06 -0.241E-02 -0.214E+00 0.460E+00 0.000E+00

43

6 -0.542E-06 -0.222E-06 -0.104E-02 0.316E+00 0.534E+00 0.000E+00

На основе полученных данных можно построить картину деформированного состояния срединной поверхности пластинки (рис. 31). В приложении 3 представлены тексты программ для выполнения всех этапов определения собственных частот и соответствующих им векторов

1 =805 Гц

2 =3632 Гц

y 2 4

6

Рис. 31

44

ПРИМЕРЫ ПРАКТИЧЕСКОГО ИСПОЛЬЗОВАНИЯ НЕКОТОРЫХ ТИПОВ КОНЕЧНЫХ ЭЛЕМЕНТОВ ПРИ ИССЛЕДОВАНИИ СТАТИЧЕСКИХ

И ДИНАМИЧЕСКИХ СОСТОЯНИЙ КОНСТРУКЦИЙ

Пространственные стержневые конструкции

При проектировании стальных ферменных конструкций считают, что жесткость узлов в местах соединения элементов фермы не существенно влияет на работу конструкции и их рассматривают как шарнирные.

Проблема заключается в необходимости более полного учета жесткостных характеристик элементов в местах их соединений и, в связи с этим, перераспределение силовых потоков.

Стальная опора (рис. 32) моделируется в виде линейноупругой стержневой пространственной конструкции, нагруженной узловыми силами, возникающими от веса проводов (с учетом покрытия их слоем льда) и ветровой нагрузки.

7

6

3

5

2

4

1

Z

X

Y

Рис. 32

45

При построении модели использовался конечный элемент в виде прямого бруса, воспринимающего в общем случае все виды нагрузок (растяжение, изгиб в двух плоскостях и кручение). В качестве узлов i, j приняты его концы (рис. 7).

Оси локальной системы координат направлены таким образом, чтобы ось X совпала с продольной осью бруса, а оси Y и Z совпадали с главными центральными осями его поперечного сечения.

В каждом узле рассматривается 6 степеней свободы (3 линейных и 3 угловых – они показаны на рис. 7 дуговыми стрелками) и соответствующие им силовые факторы. Матрица жесткости рассматриваемого конечного элемента имеет размерность 12 12. Преобразование матрицы жесткости бруса из локальной в глобальную систему координат производится в соответствии с выражением

K Т k ,

где [k] – матрица жесткости бруса в локальной системе координат;

[ ] – матрица направляющих косинусов локальных осей. Модель конструкции выполнена в соответствии с рабо-

чими чертежами опоры ВЛ 220.

Вмодели выделено 748 конечных элементов, соединенных при помощи 323 узлов. Размерность полученной системы уравнений – 1938, ширина ленты этой системы линейных алгебраических уравнений равна 222. Система уравнений решена при помощи метода Холецкого с фазовой обработкой; число уравнений, входящих в одну фазу – 600.

Врезультате решения системы уравнений получены векторы перемещений узлов в глобальной системе координат и напряжения в конечных элементах. Характер деформированного состояния опоры представлен на рис. 33.

Анализ массива напряжений в элементах позволяет выявить зоны опоры, в которых напряжения превышают допускаемые. На основании полученной информации можно сделать вывод о необходимости усиления стоек в нижней части опоры.

46

Рис. 33

47

Плоская задача теории упругости

Существует широкий класс важных в практическом отношении задач, в которых перемещения, деформации и напряжения зависят лишь от двух координат – x и y. Этот класс задач под общим названием «плоская задача теории упругости» подразделяется на плоскую деформацию и обобщенное плоское напряженное состояние.

Если в процессе нагружения все точки тела перемещаются только параллельно одной плоскости (плоскости xy, например), то соответствующее деформированное состояние называется плоской деформацией. Таким образом, для плоской де-

формации имеем ux=ux(x,y), uy=uy(x,y), uz=0.

z x

Рис. 34

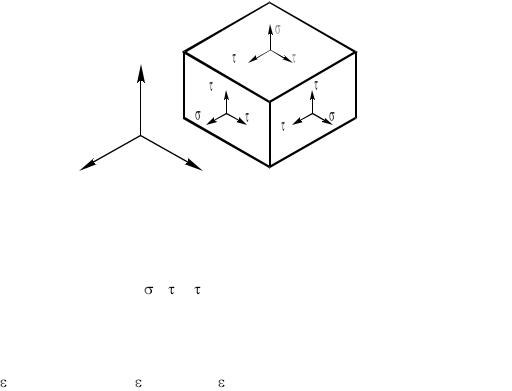
Выделим из тела элементарный параллелепипед сечениями, параллельными координатным плоскостям (рис.34). Обозначим компоненты напряжения в площадке, перпендикулярной оси x, через x, xy, xz, аналогично для других площадок. Первый индекс в этих обозначениях характеризует ориентацию площадки, а второй направление действия соответствующей составляющей напряжения.

В соответствии с уравнениями Коши, деформации xz=dux/dz+duz/dx, zz=duz/dz, yz=duz/dy+duy/dz оказываются

равными нулю.

48

Из закона Гука вытекает, что касательные напряжения

xz=G xz, yz=G yz также равны нулю (G — модуль сдвига, — относительная деформация). Остальные компоненты деформа-

ции и напряжения являются функциями только координат x и y. Если тонкая пластина, параллельная плоскости xy, нагружена объемными и по контуру — поверхностными силами, параллельными ее плоскости и равномерно распределенными по толщине, то имеет место обобщенное плоское напряженное состояние. В этом случае можно пренебречь компонентами напряжения z, xz и yz, а x, y и xy считать постоянными по

толщине:

z= xz= yz=0

x= x(x,y), y= y(x,y) и xy= xy(x,y).

Из закона Гука следует, что при обобщенном плоском напряженном состоянии деформации сдвига xz= yz=0, а остальные компоненты деформации представляются как функции только координат x и y.

Расчет по методу конечных элементов начинается с дискретизации расчетной модели. Пусть рассматриваемая область двумерна, т.е. все ее характеристики зависят от двух координат (рис. 35). Каждый конечный элемент этой области сохраняет все физические и геометрические свойства исходной среды. На границе области заданы граничные условия /1,2,3/.

Для решения плоской задачи теории упругости разработано много разнообразных конечных элементов, отличающихся друг от друга аппроксимацией перемещений и способом описания геометрии. В качестве наиболее простого рассмотрим плоский треугольный элемент с тремя узлами в углах (рис. 36). Узловые перемещения для такого элемента указаны на рисунке. Вектор перемещений для узла i состоит из двух компонент:

49