
2402
.pdf
На рис 17.1 построена полная развертка поверхности треугольной призы. Для этого надо проделать следующие действия.
1. Приведем призму в положение, когда ее ребра // оси x.
2. Пересечемпризмуплоскостью |
|
|
кбоковымребрампризмы. |
||||||||||
3. Определим проекции на |
2 |
точек 1, 2, 3. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
A0 |
|
|
|
|
B0 |
|
|
|
|
|
A0 |
||
|
|
|
|
|
|
|
|
|
|||||
|
|
B0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
C0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
10 |
|
|
20 |
|
30 |
|
|
|
10 |
|
|
||
D |
|
|
|
|
|
|
|
|
|
|
D0 |
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F0 |
||||||||
|
|
|
B2 |
|
|
|
|
|
E0 |
||||
|
|
|
|
22 |
|
|
|
E2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
12 |
|
|
D2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
F2 |
|
|||
x |
C2 |
3 |
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
C1 |
|
21 |
|
|
|
E1 |
||||
|
|
|
|
11 |
|
|
|
||||||
|
|
|
|
|
|
D1 |
|||||||
|
|
|
|
|
393 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
F1

Рис. 17.1. Развертка треугольной призмы методом нормального сечения
4.Определим стороны 123 (любым способом).
5.В свободном местек проведем горизонтальную линию
и на ней отложим стороны 123.
6. отложим отрезки 10 A0 12 A2 и т. д.
7. Строим боковые грани призмы. Развертка построена.
17.2. Способ раскатки
Если боковые грани призмы параллельны одной плоскости проекций, ребра параллельны другой применяется метод раскатки.
На рис. 17.2 показано, как получить развертку треугольной призмы этим методом.
|
|
|
10 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
20 |
|
|
|
|
|
|
|
22 |
32 |
|
|
|
|
|
40 |
60 |
||
12 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
// |
50 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
42 |
52 |
62 |
|
|
|||
11 |
|
|
41 |
|
|
|
|
|
|
|
|
|
|
|
94 |
|
61 |
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
// 31 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
51 |
|
|
|
|
|||

Рис. 17.2. Развертка треугольной призмы, полученная методом раскатки
17.3. Способ треугольников
развертки пирамидальных и конических поверхностей строят способом триангуляции (способом треугольников). Построение развертки сводится к многократному посроению истинных величин треугольников, из которых состоит поверхность развертываемлой пирамиды.
Построим развертку боковой поверхности пирамиды. Методом вращения определяем длины ребер пирамиды
и на свободном месте чертежа строим развертку. За центр вращения возьмем т. S1 (рис.17.3).
S0
C0
S2
|
|
|
|
|
|
A0 |
C0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
C2 |
|
|
C2 B |
A |
A2 |
|
B2 |
B0 |
|
|
|
C1 |
|||||
|
2 |
2 |
|
|
|
||
|
|
|
|
S1 |
|
|
|
|
C1 B1 |
A1 |
A1 |
95 |
B1 |
|
|
|
|
|
|||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|

Рис. 17.3. Развертка боковой поверхности пирамиды методом треугольников
17.4. Развертка развертывающихся поверхностей
Развертка поверхностей (кроме гранных) является приближенной, т.к. поверхность аппроксимируют поверхностями вписанных или описанных многогранников в форме прямоугольников или треугольников.
Развертка цилиндрической поверхности.
Заменим цилиндрическую поверхность многогранной призмой (рис.17.4).
Построим развертку вписанной призмы и ломанную линию аппрксимируем плавной кривой.
96

Рис. 17.4. Развертка наклонного цилиндра
Развертка конуса.
Конус заменяется вписанной многогранной пирамидой
(рис.17.5, 17.6).
Прямой конус.
гол развертки: |
2 |
r |
. l -длина образующей конуса. |
|||
l |
||||||
|
S2 |
|
|
|
||
|
|
|
|
|
||
l2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
S1
r
Рис. 17.5. Развертка прямого конуса
Наклонный конус
97

Рис. 17.6. Развертка наклонного конуса
18. КРИВЫЕ ЛИНИИ
Линия – траектория движения точки. Вопрос: Какие вы знаете линии?
Ответ: |
1) |
алгебраические |
( y f x ), |
трансцендентные ( f y F x );
F x );
2) пространственные и плоские.
Вопрос: что определяет порядок кривой?
Ответ: Количество пересечений с плоскостью или прямой.
18.1.Касательные и нормали к пространственной кривой
Касательная tM – секущая в предельном положении.
Через касательную можно провести множество плоскостей и только одна из них называется соприкасающейся плоскостью  (рис.18.1).
(рис.18.1).

Рис. 18.1. Касательные и нормали проведенные к пространственной кривой
В любой точке можно провести множество нормалей, которые определяют нормальную плоскость , и только одна
нормаль, лежащая в соприкасающейся плоскости называется главной нормалью n .
Нормаль перпендикулярная  называется бинормалью
называется бинормалью
n .
n и tM образуют спрямляющую плоскость .
, , образуют трехгранник Френе, при этом: горизонтальная плоскость;  - профильная плоскость; фронтальная плоскость.
- профильная плоскость; фронтальная плоскость.
18.1.1. Построение касательной к кривой, |
|
проходящей через т. А. |
tM |
Построениепоказано на рис. 18.2. |
|
M |
a3 |
|
A
// //
-
-
a2 a1
99

Рис. 18.2. Построение касательной к кривой, проходящей через т. А
18.1.2. Построение касательной к кривой l ,
проходящую через т.А.
Дано: l и т. А |
|
|
1. |
Проведем прямую b |
кривой и проходящую |
через т. |
A (рис.18.3). |
|
2. |
Проведем ряд секущих , пересекающих l и b |
|
( a1,a2 ,... и т. д.)
3.Отложим от прямой b вправо отрезки равные
хордам.
4.Там, где огибающая пересечет l - будет т. M , соединив ее с т. A, получим искомую касательную.
M


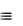 A
A
l |
/ // |
|
// |
||
|
||
|
/ |
Рис. 18.3. Построение касательной к кривой проходящей через т.А
100

18.1.3. Определение центра кривизны в т. М.
Дано: l и т. M (рис. 18.4).
1.Проведем касательные к произвольным точкам А, В,
М и С.
2.Отложим на них отрезки равной длины и соединим их
вкривую l .
.
3.В т. M  проведем касательную tM .
проведем касательную tM .
4.Проведем перпендикуляры к касательным в т. M и т. M , пересечение которых даст центр кривизны OM в т. M .
|
|
l |
|
|
M tM |
M |
|
B |
tM |
||
|
|||
A |
|
||
|
|
l
OM
Рис. 18.4. Определение центра кривизны
18.1.4. Эволюта и эвольвента
Эволюта – множество точек, являющихся центром кривизны данной прямой.
Эвольвента.
Построение эвольвенты показано на рис. 18.5. rn 1 n
rn
|
|
Эвольвента |
||
|
3 |
|
// |
|
n |
101 |
// |
||
|
||||
|
2 |
|
|
|
Эволюта |
|
/ / |
|
|
|
1 |
|
||

Рис. 18.5. Построение эвольвенты
Эвольвента нашла широкое применение в технике: профиль зубьев у шестеренок изготавливают по эвольвенте.
Свойство: касательная к эволюте является нормалью к эвольвенте.
Для зубчатого колеса эволютой эвольвенты является окружность.
18.2. Свойства кривых линий.
При построении ортогональных проекций кривых линий необходимо знать их свойства:
1.касательная к кривой проецируется в касательную к ее проекции (рис. 18.6);
2.несобственным точкам кривой соответствуют несобственные точки ее проекции.
Для плоских кривых дополнительные свойства:
3.порядок проекции кривой равен порядку самой кривой или оказывается на порядок ниже;
4.число узловых точек (т.е. точек, где кривая пересекает сама себя на проекции равно числу узловых точек на самой кривой);
5.кривая проекция кривой линии сохраняет тот же порядок, что и кривая линия, или оказывается кривой более низкого порядка.
102
