1859

УДК 517.2

Горбунов В.В. Элементы высшей математики: учеб. пособие / В.В. Горбунов, О.А. Соколова. - Воронеж: ФГБОУ ВО «Воронежский государственный технический университет»,

2017. Ч. 3. - 120 с.

В учебном пособии излагаются элементы математического анализа. Теоретический материал иллюстрируется большим количеством примеров. Содержатся вопросы для самопроверки и задачи для самостоятельного решения.

Издание соответствует требованиям Федерального государственного образовательного стандарта высшего образования по направлению 15.03.05 «Конструкторскотехнологическое обеспечение машиностроительных производств» (все профили), дисциплине «Математика».

Ил. 18. Библиогр.: 8 назв.

Научный редактор д-р техн. наук, проф. В.И. Ряжских

Рецензенты: кафедра математического моделирования Воронежского государственного университета (зав. кафедрой д-р физ.-мат. наук, проф. В.А. Костин); канд. физ.-мат. наук, доц. В.И. Кузнецова

Горбунов В.В., Соколова О.А., 2017

Оформление. ФГБОУ ВО «Воронежский государственный технический университет», 2017

ВВЕДЕНИЕ

Современное машиностроительное производство предполагает наличие высокоразвитой системы технологического обеспечения. Компьютеризация конструкторскотехнологической подготовки требует наличие хорошей математической подготовки.

Данное пособие продолжает серию пособий по высшей математике и посвящено изучению следующих разделов: неопределенные интегралы, определенные интегралы, комплексные числа, дифференциальные уравнения.

Пособие имеет следующую структуру. В начале каждого параграфа приводятся соответствующие теоретические сведения (определения основных понятий, уравнения, формулы, правила, признаки, методы). Затем следуют примеры решения типовых задач различной степени трудности и вопросы для самопроверки. Далее предлагаются задачи для самостоятельного решения. Ко всем задачам даны ответы.

Учебное пособие соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 15.03.05 «Конструкторскотехнологическое обеспечение машиностроительных производств».

3

1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

1.1. Первообразная. Неопределённый интеграл

Интегральное исчисление решает задачу нахождения функции F(x) по известной производной этой функции

F ′(x)= f (x).

Функция F(x) называется первообразной для функции f (x) на интервале (a,b), если для любого x (a,b) выполняется равенство F ′(x) = f (x) или dF(x)= f (x)dx .

Например, функция F(x)= x33 является первообразной

для функции f (x)= x2 на всей числовой прямой, так как при любом значении аргумента

f (x) на некотором промежутке (a,b), то любая другая первообразная для функции f (x) на этом промежутке может быть представлена в виде F(x)+C , где C − произвольная постоянная.

Множество всех первообразных функций F(x)+C для исходной функции f (x) называется неопределенным интегра-

4

тегрирования, ∫−знаком неопределенного интеграла.

Таким образом, по определению

∫ f (x)dx = F(x)+C .

Операция нахождения неопределенного интеграла от функции f (x) называется интегрированием этой функции.

Геометрически неопределенный интеграл соответствует множеству кривых y = F(x)+C , каждая из которых называет-

ся интегральной кривой.

y

y = F(x)+C3 y = F(x)+C2

Рис. 1

Функция, имеющая первообразную, называется интегри-

руемой.

Имеется теорема, согласно которой для интегрируемости функции достаточно ее непрерывности.

Правильность выполнения интегрирования достаточно легко проверить, продифференцировав результат, и получить при этом подынтегральную функцию. Например,

∫ctgxdx = ln sin x +C, так как (ln sin x +C)′ = ctgx ;

1.2. Таблица неопределённых интегралов

Пользуясь тем, что интегрирование есть операция обратная дифференцированию, можно получить таблицу основных интегралов:

xa+1

1.∫xa dx = a +1 + c (a ≠ −1);

2.∫xdx = 2 1x + c ;

6. ∫ex dx = ex + c ;

7. ∫sin xdx = −cos x + c ;

8. ∫cos xdx = sin x + c ;

9. ∫cosdx2 x = tgx + c ; 10. ∫sindx2 x = −ctgx + c ;

12.∫ 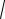a2dx− x2 = arcsin ax + c ;

13.∫1+dxx2 = arctgx + c ;

15. ∫ x2dx± a2 = ln x + x2 ± a2 + c ;

В простых случаях неопределенный интеграл с помощью тождественных преобразований подынтегральной функции и использования свойств интеграла приводится к одному или нескольким табличным интегралам, что называется непосредст-

венным интегрированием.

1.3. Основные свойства неопределённого интеграла

Основные свойства неопределенного интеграла вытекают непосредственно из его определения.

1. Производная от неопределённого интеграла равна подынтегральной функции:

(∫ f (x)dx)′ = f (x).

Действительно, (∫ f (x)dx)′ = (F(x)+C)′ = F ′(x)= f (x).

2. Дифференциал от неопределённого интеграла равен подынтегральному выражению:

d ∫ f (x)dx = f (x)dx .

Действительно,

d ∫ f (x)dx = d[F(x)+C]= dF(x)= F ′(x)dx = f (x)dx .

3. Неопределенный интеграл от дифференциала некоторой функции равен сумме данной функции F(x) и произвольной постоянной:

∫dF(x)= F(x)+C .

Действительно: ∫dF(x)= ∫F ′(x)dx = ∫ f (x)dx = F(x)+C .

4. Постоянный множитель можно выносить за знак неопределённого интеграла:

∫af (x)dx = a∫ f (x)dx .

Действительно:

(∫af (x)dx)′ = af (x) и (a∫ f (x)dx)′ = a(∫ f (x)dx)′ = af (x).

5. Неопределённый интеграл от алгебраической суммы двух функций равен сумме неопределённых интегралов от слагаемых функций:

∫[f (x)+ g(x)]dx = ∫ f (x)dx + ∫g(x)dx .

8

6. Если ∫ f (x)dx = F(x)+C , то и ∫ f (u)du = F(u)+C , где

u =ϕ(x)− произвольная функция, имеющая непрерывную про-

изводную (Свойство инвариантности формулы интегрирования).

Формула для неопределенного интеграла не меняется в зависимости от того, что используется в качестве переменной интегрирования, независимая переменная или любая ее непре- рывно-дифференцируемая функция.

∫(tgx)5d(tgx)= (tgx6 )6 +C , или,

поменяв x на ln x , получим

∫(ln x)5d(ln x)= (ln6x)6 +C .

7.Если ∫ f (x)dx = F(x)+C , то ∫ f (ax)dx = a1 F(ax)+C .

Действительно:

8. Если ∫ f (x)dx = F(x)+C , то ∫ f (x +b)dx = F(x +b)+C .

9. Если ∫ f (x)dx = F(x)+C , то ∫ f (ax +b)dx = a1 F(ax +b)+C .

Пример 1.3.1. Найти ∫cos(x +3)dx .

Решение: ∫cos(x +3)dx = sin(x +3)+C .

Пример 1.3.2. Найти ∫cos(2x)dx .

9