Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1859

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

953.53 Кб

Скачать

☆

<<< < Предыдущая 12 / 132 3 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Решение: ∫cos(2x)dx = 12 sin(2x)+C .

Пример 1.3.3. Найти ∫cos(4x +5)dx .

Решение: ∫cos(4x +5)dx = 14 sin(4x +5)+C .

Пример 1.3.4. Найти ∫6x1+1 dx .

Решение: ∫6x1+1 dx = 16 ln(6x +1)+C .

1.4. Замена переменной в неопределенном интеграле

Одним из основных методов интегрирование является метод замены переменной.

Пусть требуется найти интеграл ∫ f (x)dx , причем непо-

средственно подобрать первообразную для f (x) мы не можем,

но нам известно, что она существует.

Сделаем замену переменной в подынтегральном выражении, положив x =ϕ(t). Тогда dx =ϕ′(t)dt и

∫ f (x)dx = ∫ f (ϕ(t))ϕ′(t)dt .

Функцию x =ϕ(t) следует выбирать так, чтобы можно

было вычислить неопределенный интеграл, стоящий в правой части равенства.

В некоторых случаях целесообразнее подбирать замену переменного не в виде x =ϕ(t), а t =ψ(x).

Пусть вычисляется интеграл ∫ψψ′((xx))dx .

Заменяем ту функцию, стоящую под интегралом, производную от которой мы видим под этим же интегралом.

Положим ψ(x)= t ,

тогда dψ(x)= dt ;

ψ (x)dx = dt . Под-

′

ставляя

интеграл,

полу-

чим∫

ψ ′(x)

dx = ∫dtt

= ln

+C = ln

ψ(x)

+C .

ψ(x)

Пример 1.4.1. Найти ∫esin x cos xdx .

Решение: Пусть t = sin x , тогда dt = d sin x ; dt = cos xdx . Тогда

∫esin x

cos xdx = ∫et dt = et

+C = esin x +C .

Пример 1.4.2. Найти

∫

dx .

x3 −5

Решение: Пусть t = x3 −5 , тогда dt = d(x3 −5);

dt = 3x2 dx ;

dx =

dt .

Тогда ∫

dx =

∫

−5

+C .

−

Пример 1.4.3. Найти

∫

arctg 2 x

dx .

Решение: Пусть t = arctgx , тогда dt = d(arctgx)

;

dt =

dx .

x2 +1

arctg 2 x

Тогда ∫

dx = ∫t

dt = t

+C = arctg

x +C .

Пример 1.4.4. Найти

∫

dx .

cos2 x(tg 2 x + 4)

Решение: Пусть t = tgx , тогда dt = d(tgx);

dt =

dx .

cos2 x

Тогда

tgx

∫

dx =

∫

2 arctg

+C = 2 arctg

+C .

cos2 x(tg 2 x + 4)

t 2

+ 4

Пример 1.4.5. Найти

∫

dx .

x(ln2 x −9)

Решение: Пусть t = ln x , тогда dt = d(ln x); dt =

1 dx .

Тогда

t −3

ln x −3

∫

dx = ∫

+C =

6 ln

ln x +3

+C .

x(ln2 x −9)

t 2 −9

2 3

t +3

Как отмечалось выше, вид неопределённого интеграла не зависит от выбора аргумента интегрирования, что используется при интегрировании способом введения новой функции под знак дифференциала. В данном варианте метода новая переменная интегрирования не обозначается новым символом, а берется в скобки для наглядности.

Пример 1.4.6. Найти ∫lnxxdx .

Решение:

∫lnxxdx = ∫ln x dxx = ∫(ln x)d(ln x)= (ln2x)2 +C .

Пример 1.4.7. Найти ∫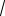sin x cos xdx .

Решение:

	1			3 / 2	3
∫		cos xdx = ∫(sin x)2 d(sin x)=	(sin x)		+C = 2(sin x)	2	+C
	sin x		(sin x)			2
	sin x
	3				3
	2
		1.5. Правило интегрирования по частям
	Пусть функции u = u(x) и v = v(x)			имеют непрерывные
производные. Тогда d(uv)= vdu +udv .

Интегрируя обе части равенства по x , имеем:

∫d(uv)= ∫vdu +∫udv , uv = ∫vdu + ∫udv или

∫udv = uv − ∫vdu .

Эта формула называется формулой интегрирования по частям. Формула сводит вычисление интеграла∫udv к вычис-

лению интеграла ∫vdu , которое может оказаться проще исход-

ного.

Интегрирование по частям требует представление подынтегрального выражения в виде произведения множителей u и dv . Существуют три типа интегралов, в которых по разным соображениям происходит выбор множителей u и dv в подынтегральных выражениях.

В интегралах

первого

типа

∫Pn (x)ekx dx ; ∫Pn (x)akx dx ;

∫Pn (x)sin kxdx ;

∫Pn (x)cos kxdx , где Pn (x)−многочлен n-ой сте-

пени,

k −число; в качестве u выбирается многочлен Pn (x), а в

качестве dv −все остальные сомножители.

Пример

1.5.1.

Вычислить

неопределенный

интеграл

∫xex dx , используя метод интегрирования по частям.

Решение:

u = x

du = dx

∫

== xex −

∫

ex dx = xex −ex +C.

xex dx =

v = e

dv = e

Пример

1.5.2.

Вычислить

неопределенный

интеграл

∫x cos3xdx .

Решение:

u = x

= dx

sin 3x −1 ∫sin 3xdx =

∫x cos3xdx =

v =

dv = cos3xdx

sin 3x

1 cos3x +C .

sin 3x +

В некоторых интегралах приходится несколько раз интегрировать по частям.

Пример 1.5.3. Вычислить неопределенный интеграл

∫x2e5x dx .

Решение:

u = x

du = 2xdx

∫x

∫xe

dx =

dx,

v =

−

dx =

dv = e

Применим ко второму интегралу еще раз формулу интегрирования по частям, имеем

u = x,

du = dx

∫xe

−

dx =

dv = e5x dx, v =

1 e5x

2 x

∫e

−

5 5

2 x

−

+C =

5 5

−

2xe5x

+C .

125

∫Pn (x)arcsin xdx ,

интегралах

второго

типа

∫Pn (x)arccos xdx ,

∫Pn (x)ln xdx ,

∫Pn (x)arctgxdx ,

∫Pn (x)arcctgxdx удобно положить dv = Pn (x)dx, а в качестве u выбрать оставшиеся сомножители.

Пример 1.5.4. Вычислить неопределенный интеграл

∫x4 ln xdx .

Решение:

						dx
			u = ln x, du =				x
∫x	4	ln xdx =					x		=
∫x		ln xdx =		4			x	5	=
			dv = x		dx, v =
			dv = x		dx, v =		5
							5

x5	ln x − ∫	x5	dx	=
5
	5		x


=	x5	ln x − 1 ∫x4 dx =		x5	ln x −	x5	+C .

5		5	5		25
В		интегралах	третьего				типа ∫enx sin mxdx ;
∫anx sin mxdx ; ∫enx cos mxdx ;					∫anx cos mxdx в качестве u выби-

рается enx или anx . После двукратного интегрирования по частям решается уравнение относительно исходного интеграла.

Пример 1.5.5. Вычислить неопределенный интеграл

∫ex sin xdx .

Решение:

∫e

u = ex ,

du = ex dx

= −e

cos x +

sin xdx =

dv = sin xdx, v = −cos x

+ ∫e

u = ex ,

du = ex dx

= −e

cos x

+ e

sin x −

cos xdx =

dv = cos xdx,v = sin x

− ∫ex sin xdx.

Получили нетривиальный результат - уравнение относительно исходного интеграла. Обозначив его за J , получим уравнение

J = e x (sin x − cos x)− J.

Перенося J в левую часть уравнения, имеем

2J = e x (sin x − cos x).

Окончательно: ∫ex sin xdx = ex (sin x −cos x)+C . 2

1.6. Интегралы от некоторых функций, содержащих квадратный трехчлен

1. Рассмотрим интеграл I1	=		dx	.
		∫ax2	+bx + c

Преобразуем квадратный трехчлен, стоящий в знаменателе, в сумму или разность квадратов, предварительно выделив из него полный квадрат суммы или разности.

x +

+bx

+ c = a x

= a

+ 2

−

= a

x +

−

Таким образом, интеграл I1

принимает вид табличного

интеграла:

I1 =

∫ax

2 +bx + c

a ∫

b 2

x +

−

Пример 1.6.1.

∫

= ∫

3x + 7

+ 2x

−

+ 7

(2x

arctg

+C .

Рассмотрим интеграл I2

∫

2 +bx + c

Вычисляется также как и интеграл I1 .

Пример 1.6.2.

∫

= ∫

7 − x2 −6x

−(x2 + 2x 3 +9 −9 −7)

16 −(x +3)2

= arcsin

x +3

+C .

Рассмотрим интеграл I3 =

Ax + B

dx .

∫ax2 +bx + c

Сделаем

замену

переменной

ax2 +bx + c = t . Тогда

d(ax2 +bx + c)= dt ;

(2ax +b)dx = dt .

Произведем тождествен-

ное преобразование подынтегральной функции так, чтобы в

числителе получить выражение

(2ax +b).

Ax + B

(2ax +b)−

Ab + B

I3 =

dx . Разобъем по-

∫ax

2 +bx + c

∫

ax2 +bx + c

лученный интеграл на сумму двух интегралов.

Таким образом, получаем

(2ax +b)− Ab + B

2ax +b

∫

dx =

∫

+bx + c

∫

−

∫

+ B

−

+ bx + c

+bx + c

−

+C .

Пример 1.6.3.

(x +8)dx

Вычислить I

= ∫

+ 4x +5

Введем замену переменной

+ 4x +5 = t ;

d(x2 + 4x +5)= dt ;

(2x + 4)dx = dt . Тогда

(x +8)dx

1 (2x

+ 4)− 2 +8

(2x

+ 4)dx

= ∫

dx =

∫

+ 4x +5

+ 6∫

= 1 ∫dt

+ 6∫

+ 4x +5

+ 2x 2 + 4 − 4 +5

1 ln

+ 6∫

1 ln

4x +5

+ 6arctg(x + 2)+C .

(x +

+ B

dx .

Рассмотрим интеграл

∫ ax2 +bx

+ c

Вычисляется также как и интеграл I3 .

Пример 1.6.4.

(x −3)dx

Вычислить I = ∫

+8x +10

Введем

замену

переменной

x2 +8x +10 = t ;

(x2

+8x +10)= dt ; (2x +8)dx = dt . Тогда

(x −3)dx

1 (2x +8)−7

(2x +8)dx

I = ∫

= ∫

dx =

∫

−

+8x +10

x +8x +10

−

7∫

1 ∫dt −

7∫

+8x +10

+ 2x

4 +16 −16 +10

1 ln

−7∫

1 ln

+8x +10

−

(x + 4)

−

−7∫

= 1 ln

−7 ln

(x +4)+

+C .

+8x +10

(x +4)2 −6

(x + 4)

−6

1.7. Дробно-рациональные функции. Простейшие рациональные дроби и их интегрирование

Дробно - рациональная функция или рациональная дробь

R(x)=	P (x)		a		+ a x + a		x2	+... + a		xn
	n	=		0	1	2			n
	Qm (x)
			b0 +b1x +b2 x2 +... +bm xm

называется правильной, если степень числителя n меньше степени знаменателя m . Если n ≥ m , то рациональная дробь н а-

зывается неправильной.

Всякую неправильную дробно-рациональную функцию путём деления числителя на знаменатель всегда можно пред-

ставить в виде суммы многочлена N(x) и правильной рацио-

нальной дроби: R(x)= N(x)+ Pk ((x)) (k < m).

Qm x

Пример 1.7.1. Представить неправильную рациональную

дробь	x3	+ 4	в виде суммы целой части от деления (мно-
	x2 −	7x +9

гочлена) и правильной рациональной дроби Решение: Разделив числитель на знаменатель, выделим

целую часть:

x3 + 4

x2 − 7x + 9

x3 −7x2 +9x

x + 7

−

40x −59

x2 − 7x + 9

_ 7x

−9x + 4

7x2

− 49x + 63

_ 40x −59

40x −59

В результате получим

x3 + 4

= x + 7

−

40x −59

x2 −7x +9

x2 − 7x +

Интегрирование многочлена не представляет труда, поэтому рассмотрим интегрирование правильной рациональной дроби.

<<< < Предыдущая 12 / 132 3 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.2022939.61 Кб01826.pdf
#
15.11.2022945.83 Кб11837.pdf
#
15.11.2022949.61 Кб01846.pdf
#
15.11.2022951.12 Кб31848.pdf
#
15.11.2022951.95 Кб21851.pdf
#
15.11.2022953.53 Кб01859.pdf
#
15.11.2022962.02 Кб11866.pdf
#
15.11.2022973.22 Кб31874.pdf
#
15.11.2022974.25 Кб11876.pdf
#
15.11.2022975.2 Кб11877.pdf
#
15.11.2022977.75 Кб51880.pdf