1859

Общее решение соответствующего однородного уравне-

ния имеет вид yoo = C1ex +C2e−2x .

Правая часть данного неоднородного уравнения имеет

вид

f (x) = eαx (M cos βx + N sin βx) .

Так как число α +iβ = i не является корнем характеристического уравнения, то частное решение будем искать в

форме yчн = (Acos x + B sin x) .

Находя производные и подставляя их в исходное уравне-

ние, получим (B −3A) cos x + (−A −3B)sin x = cos x −3sin x.

Отсюда С1=1, С2=0. Искомое частное решение будет иметь вид y = e x + sin x .

5.13. Метод вариации произвольных постоянных

Частное решение yчн .уравнения y′′+ a1(x)y′+ a2 (x)y = f (x) с правой частью произвольного вида можно найти, если из-

вестно общее решение yoo соответствующего однородного урав-

нения методом вариации произвольных постоянных.

За основу берется общее решение однородного дифференциального уравнения yoo = c1 y1 (x)+ c2 y2 (x). Заменим в

110

общем решений постоянные c1 и c2 неизвестными функциями c1(x) и c2 (x) и подберем их так, чтобы функция

y = c1 (x)y1 (x)+ c2 (x)y2 (x) была решением исходного неоднородного дифференциального уравнения. Для определения

функций c1(x) и c2 (x) найдем первую производную y′

y′ = c1′(x)y1 (x)+ c1 (x)y1′(x)+ c2′ (x)y2 (x)+ c2 (x)y2′ (x).

Поскольку введены две новые функции, то появляется возможность наложить некоторое условие на эти функции. По-

требуем, чтобы c1′(x)y1 (x)+ c'2 (x)y2 (x)= 0 .

Тогда y′ = c1 (x)y1′(x)+ c2 (x)y2′ (x),

y′′ = c1′(x)y1′(x)+ c1 (x)y1′′(x)+ c2′ (x)y2′ (x)+ c2 (x)y2′′(x).

Подставляя выражение для у, y′и y′′ в исходное уравнение, получим:

c1′(x)y1′(x)+ c1 (x)y1′′(x)+ c2′ (x)y2′ (x)+ c2 (x)y2′′(x)+

+ a1(x)[c1(x)y1′(x)+c2 (x)y2′ (x)]+ a2 (x)[c1(x)y1(x)+c2 (x)y2 (x)]= f (x)

или

c1 (x)[y1′′(x)+ a1 (x)y1′(x)+ a2 (x)y1 (x)]+

+c2 (x)[y2′′(x)+a1 (x)y2′ (x)+a2 (x)y2 (x)]+c1′(x)y1′ +c2′ (x)y2′ (x)= f (x).

Поскольку y1(x) и y2 (x) - частные решения уравнения

y′′+ a1 (x)y′+ a2 (x)y =0,

то выражения в ква дратных скобках равны нулю, а п оэтому

c1′(x)y1′(x)+ c2′ (x)y2′ (x)= f (x).

Функция y = c1 (x)y1 (x)+ c2 (x)y2 (x) будет частным реше-

нием уравнения y′′+ a1(x)y′+ a2 (x)y = f (x), если функции c1(x)и с2(х) удовлетворяют системе уравнений:

c1′(x)y1 (x)+ c2′ (x)y2 (x)= 0,c1′(x)y1′(x)+ c2′ (x)y2′ (x)= f (x).

111

ся определителем Вронского для фундаментальной системы частных решений y1(x) и y2 (x) однородного дифференциального

Вопросы для самопроверки

1.Дайте определение дифференциального уравнения первого порядка, его общего и частного решения.

2.Что представляет собой интеграл дифференциального уравнения?

3.Сформулируйте задачу Коши для дифференциального

уравнения первого порядка и укажите ее геометрический смысл.

4. Дайте определение дифференциального уравнения с разделяющимися переменными, укажите метод его решения.

5. Дайте определение однородного дифференциального уравнения.

6. Опишите метод Бернулли решения линейного дифференциального уравнения первого порядка.

7. Перечислите типы дифференциальных уравнений второго порядка, допускающих понижение порядка.

113

8. Выведите формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае действительных различных корней характеристического уравнения.

9.Каково общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае равных корней характеристического уравнения.

10.Каково общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае комплексных корней характеристического уравнения. Приведите примеры.

11.Каково общее решение неоднородного дифференци-

ального уравнения второго порядка.

12. Изложите правило для нахождения частного решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами и правой частью

видаeαx Pn (x) , где Pn (x) есть многочлен степени n ≥ 0.

13. Изложите правило для нахождения частного решения линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами и правой частью

вида eαx (Acos βx + B sin βx) .

Задачи для самостоятельного решения

Найти общее решение дифференциального уравнения первого порядка.

Найти частное решение дифференциального уравнения первого порядка, удовлетворяющее заданным начальным условиям

Ответ: y = 53 e x3 − 13 (2 + x3 ).

Найти общее решение дифференциального уравнения, допускающего понижение порядка.

13. 2xyy′′ = ( y′)2 +1. Ответ: y = 3C21 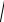(C1 x −1)3 +C2 .

115

14 yy′′− yy′ln y = ( y′)2 . Ответ: x +2C2 = C1arctg(C1 ln y).

Найти частное решение линейного неоднородного дифференциального уравнения второго порядка, удовлетворяющее начальным условиям.

Ответ: y = e x (0,16 cos 3x +0,28sin 3x) + x 2 +2,2x +0,84.

17. y′′− y′ = 2(1− x); y x=0 =1, y′ x=0 =1.

Ответ: y = e x + x 2 .

116

ЗАКЛЮЧЕНИЕ

Рассмотренные разделы высшей матаматики являются базовыми и входят в обязательный перечень тем, необходимых для успешного освоения специальных дисциплин по направлению 15.03.05 «Конструкторско-технологическое обеспечение машиностроительных производств».

БИБЛИОГРАФИЧЕСКИЙ CПИСОК

1.Бугров Я.С. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного / Я.С. Бугров, С.М. Никольский. М.: Наука, 1981.

2.Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов / Н.С. Пискунов. М.: Наука, 1985. Т. 1.

3.Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов / Н.С. Пискунов. М.: Наука, 1985. Т. 2.

4.Толстов Г.П. Элементы математического анализа / Г.П. Толстов. М.: Наука, 1974. Т. 1.

5.Толстов Г.П. Элементы математического анализа / Г.П. Толстов. М.: Наука, 1974. Т. 2.

6.Кудрявцев В.А. Краткий курс высшей математики / В.А. Кудрявцев, Б.П. Демидович. М.: Наука, 1975.

7.Данко П.Е. Высшая математика в упражнениях и задачах: учеб. пособие для втузов / П.Е. Данко, А.Г. Попов, Т.Я.

Кожевникова. М.: Высш. шк., 1996. Ч. 1.

8. Данко П.Е. Высшая математика в упражнениях и задачах: учеб. пособие для втузов / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. М.: Высш. шк., 1996. Ч. 2.

117

ОГЛАВЛЕНИЕ

Введение…….……………………………….….………………...3 1. Неопределенный интеграл…….…………………………..... ..4

1.1.Первообразная. Неопределенный интеграл…. ……… 4

1.2.Таблица неопределенных интегралов ……….……….6

1.3.Основные свойства неопределенного интеграла …....8

1.6.Интегралы от некоторых функций, содержащих квадратный трехчлен………………………..…….….16

1.7. Дробно – рациональные функции. Простейшие рациональные дроби и их интегрирование………..19

1.8. Разложение правильной дробно – рациональной функции на сумму простейших дробей……….…....20

1.9. Интегрирование тригонометрических выражений…23

1.10. Интегрирование иррациональных функций……….28 Вопросы для самопроверки……………..…………..33 Задачи для самостоятельного решения………..……34

2. Определенный интеграл….……………..………………… ..37 2.1. Задача, приводящая к понятию определенного

интеграла………………………………………………37

2.2.Свойства определенного интеграла ………………. 39

2.3.Определенный интеграл с переменным верхним пределом…………..…………………………………..42

2.4Формула Ньютона – Лейбница………………………..44

2.5.Интегрирование по частям в определенном

интеграле……………………………………………….46

2.6.Замена переменной в определенном интеграле ……47

2.7.Несобственные интегралы. Несобственные интегралы первого рода……….………………………49

2.8.Несобственные интегралы второго рода…...……......51 Вопросы для самопроверки….…….…………………...53

Задачи для самостоятельного решения….…….……….53

118

3. Приложения определенного интеграла………………....…...56

3.1.Площадь плоской фигуры в декартовых координатах.56

3.2.Площадь фигуры, ограниченной кривой, заданной

параметрическими уравнениями…………………........58 3.3 Площадь криволинейного сектора в полярной

системе координатах……………………………………..59 3.4. Вычисление длины дуги…….………………………….62 3.5. Вычисление объема тела…...……..……………………66

3.6. Вычисление площади поверхности вращения…...…...67

3.7. Работа переменной силы……...………….…………….70

Вопросы для самопроверки…..………………………..71 Задачи для самостоятельного решения………..………72 4. Комплексные числа………………………...……………........73

4.1.Основные понятия……………..………………………..73

4.2.Три формы записи комплексных чисел…..……………74

4.3.Действия над комплексными числами……..…….…....77 Вопросы для самопроверки……..…………………..…83

Задачи для самостоятельного решения……………..…84

5. Дифференциальные уравнения……..…………….…………85

5.1. Основные понятия…………..…..………………………85

5.2. Дифференциальные уравнения первого порядка.

Основные понятия…………………….…………………85 5.3. Уравнения с разделяющимися переменными..………. 87 5.4. Однородные уравнения первого порядка……………...89 5.5. Линейные дифференциальные уравнения первого

порядка…..………………………………………………91 5.6. Уравнения Бернулли……………………...……….…….93 5.7. Дифференциальные уравнения высших порядков.

Основные понятия…………………………………… .93 5.8. Некоторые типы дифференциальных уравнений

второго порядка, приводящиеся к уравнениям первого порядка…………………………………………………..94

5.9. Линейные однородные дифференциальные уравнения второго порядка…………………………………97

119