1465

С учетом (2.64) получим

Таким образом, при таком деформировании можно найти еще 1 компоненту тензора линейно-упругих свойств материала с ГПУ-решеткой – C1212 . Остается найти еще 4 компоненты.

Рассмотрим простой сдвиг образца в плоскости, перпендикулярной

Следовательно, в этих двух опытах можно найти оставшиеся 4 компоненты тензора линейно-упругих свойств материала с ГПУ-решеткой –

C1332 , C2323 , C2332 , C3232 .

При простом сдвиге образца в плоскости, перпендикулярной оси Ox3, в направлении Ox2 ( ( u)23= γ , ( u)ij= 0 ), а также в опыте на простой сдвиг, для которого ( u)32= γ , ( u)ij= 0 , упругий закон принимает

вид (все компоненты уже известны, этот опыт может использоваться для их проверки)

151

Итак, с помощью 5 экспериментов можно найти все 11 независимых ненулевых компонент тензора линейно-упругих свойств материала с ГПУ-решеткой.

Задания:

1)Выполнить анализ структуры тензора линейно-упругих свойств для двумерного материала с решеткой графена.

2)Выполнить аналогичный анализ для материала с решеткой графита.

3)Реализовать перечисленные опыты для получения значений упругих модулей образца с ГПУ-решеткой.

2.3. УЧЕТ ТЕМПЕРАТУРЫ. ЗАВИСИМОСТЬ МЕХАНИЧЕСКИХ СВОЙСТВ КОНДЕНСИРОВАННЫХ СРЕД ОТ ТЕМПЕРАТУРЫ

Наиболее распространенным методом теоретического исследования термомеханических свойств конденсированных сред является метод молекулярной динамики (МД). При этом, как было показано ранее, для каждой частицы (атома или молекулы) решаются уравнения движения (уравнения баланса количества движения, а в некоторых случаях и момента количества движения), содержащие силы (и моменты) взаимодействия выбранной частицы со всеми остальными частицами тела или с частицами из некоторой ее окрестности. Силы взаимодействия частиц вводятся с помощью потенциалов межатомного взаимодействия, которые являются ядром дискретных подходов и представляют собой приближенный способ описания взаимодействия частиц материала, качественно отражающий основные свойства атомов отталкиваться на малых и притягиваться на больших расстояниях. Получаемые количественные результаты зависят от числовых значений параметров потенциалов. Метод МД хорошо работает для тел малых размеров, ограничения на размеры моделируемых тел накладываются возможностями вычислительной техники и приме-

152

няемых алгоритмов. Например, использованием тех или иных методов «распараллеливания» расчетов значительно расширяют возможности МД при исследовании больших систем.

Рассмотрим, как в предложенной модификации метода атомарной статики, позволяющей провести идентификацию параметров потенциала межатомного взаимодействия для кристаллических материалов с различного типа решетками (ГЦК-, ОЦК-, ГПУ-решетками графена и графита) по их макроскопическим параметрам – равновесному межатомному расстоянию и упругому модулю сдвига. В основе этой методики лежит рассмотрение статики взаимодействующих частиц при явном задании структуры кристаллической решетки. Возможности подхода были продемонстрированы на примере использования степенных потенциалов ЛеннардДжонса и Ми. Это обосновано тем, что при исследовании механических свойств нет необходимости рассматривать процессы, идущие при сверхнизких температурах или при скоростном деформировании, когда важную роль во взаимодействии атомов могут играть квантовые эффекты, учитываемые в потенциалах специального вида. Использование статической постановки позволяет получить аналитическое решение задачи определения равновесного межатомного расстояния для различных кристаллических решеток и образцов различного размера. При этом точные значения межатомного расстояния получаются для объемов материала с небольшим числом атомов N на ребре образца (от 3 до 20). Далее для перехода на макроуровень по этим точным решениям можно сделать предельный переход, устремив число атомов на ребре образца к бесконечности. В частности, это позволяет проводить идентификацию параметров потенциала по известным макроскопическим физико-механическим свойствам материалов.

Ранее не обсуждался вопрос об учете температуры при определении механических свойств монокристаллических твердых тел. В данном разделе рассмотрим, как можно задавать температуру в статическом подходе. При моделировании поведения механических свойств различных тел методом молекулярной динамики температура вводится через кинетическую энергию движения атомов относительно среднего движения тела. При стабилизации системы энергия крупномасштабного движения атомов переходит в мелкомасштабные колебания с меньшей амплитудой (рис. 2.24). Под крупномасштабным движением здесь понимается изменение со временем положений атомов относительно центра масс системы, перемещения атомов при этом превышают среднее межатомное рас-

153

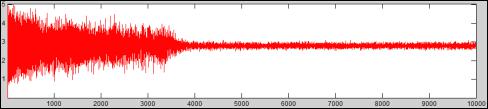
стояние. Мелкомасштабные колебания характеризуются перемещениями атомов относительно некоторых стационарных центров на величины, значительно меньшие среднего расстояния между такими центрами. На рисунке показаны результаты расчета изменения кинетической энергии системы, отнесенной к числу атомов, при эволюции из начального состояния. Начальные условия соответствовали нулевыми скоростями, но увеличенным по сравнению с равновесным периодом решетки межатомным расстоянием. То есть в систему вносилась дополнительная внутренняя энергия, вначале – за счет потенциальной энергии, далее вследствие консервативности системы, потенциальная энергия переходит в кинетическую. Кинетическая энергия менялась в крупномасштабном движении за счет последовательности прохождения волн сжатия и расширения. Затем крупномасштабные колебания уменьшались при сохранении среднего значения кинетической энергии системы. На графике зависимости кинетической энергии от времени расчета (см. рис. 2.24) виден момент перехода энергии от крупномасштабного движения к колебаниям отдельных атомов вблизи некоторых фиксированных во времени положений. Эти мелкомасштабные колебания относительно не меняющихся со временем центров отождествляются с тепловым движением и с помощью выражения E = kT , где E – амплитуда пульсаций кинетической энергии, k – постоянная Больцмана, определяется температура тела T. В статическом подходе нет возможности вводить температуру таким образом. Можно было бы считать, что статический подход дает возможность определять положения центров, относительно которых атомы совершают колебательное движение, независимое от перемещений атомов, связанных с механическим движением или деформированием тела. Тогда температуру в статическом подходе можно учесть с помощью переопределения параметров потенциала введением в них коэффициента термического расширения.

Рис. 2.24. Зависимость удельной кинетической энергии системы атомов образца

сГЦК-решеткой (40 атомов на ребре) от числа шагов в процессе перехода

кравновесному состоянию. Полная энергия системы сохраняется

154

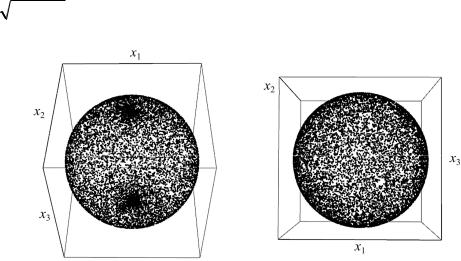
Можно пойти и по другому пути – имитировать тепловые колебания атомов с некоторой заданной амплитудой. Это можно реализовать наложением на систему атомов случайных смещений с этой амплитудой при равномерном распределении направления смещений в пространстве. Частота этих смещений (колебаний) в таком подходе рассматривается как независимый параметр, требующий идентификации для конкретного материала (подобно частоте Дебая). Для корректного задания отклонений атомов необходимо гарантировать равномерное распределение направления случайных смещений в пространстве. Направление задается единичным вектором, то есть задача сводится к нахождению равномерного распределения точек на сфере единичного радиуса.

Алгоритм получения равномерного распределения точек по сфе-

ре. В сферической системе координат равномерное разбиение интервалов

трации точек на полюсах сферы (рис. 2.25, а). Связь декартовых и сферических координат имеет вид: x1 = r cos θ cos ϕ , x2 = r cos θ sin ϕ , x3 = r sin θ .

Для того чтобы концентрации не происходило, разбивать необходимо не

сферы точками (рис. 2.25, б).

а б

Рис. 2.25. Виды распределений точек по единичной сфере, полученные при равномерном разбиении интервала для угла θ [−π / 2;π / 2] (а), при равномерном разбиении интервала [−1;1] значений функции sin θ (б)

155

Реализацию каждого из алгоритмов представим в виде набора команд для пакета «Mathematica». Для первого алгоритма используем список положений точек на единичной сфере “positions1”. Заполним его:

“positions1={}; r=1; Do[φ = Random[Real,

{ − π , π }]; θ = Random[Real,{0, 2π }]; 2 2

positions1=Append[positions1, r{Cos[θ]Cos[φ], Sin[θ]Cos[φ],Sin[φ]}],{5000}]”.

Для покрытия сферы точками согласно второму алгоритму используем переменную “positions2” и вспомогательную переменную “sinφ”:

“positions2={}; r=1; Do[sinφ=Random[Real, {–1, 1}]; θ = Random[Real, {0, 2π }];

positions2=Append[positions2, r{Cos[θ] 1 − sinφ2 ],

Sin[θ] 1 − sinφ2 ], r sinφ}], {5000}]”.

Для графического представления полученных распределений необходимо выполнить команду (нижний индекс в пакете задается с помощью нажатия комбинации клавиш "Ctrl+_"), например, для positions1:

“Show[Graphics3D[Point/@positions1]], Axes→ True, Ticks→ False,

AxesLabel → {"X1", "X2", "X3"}]”.

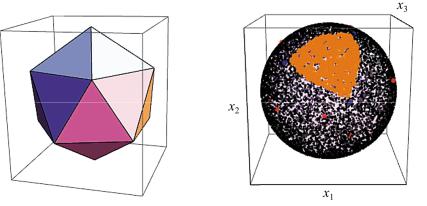
Проверим, действительно ли такой способ дает равномерное распределение точек по сфере. Для этого проведем разбиение сферы на области равной площади, совокупность которых полностью покрывает сферу. Эта задача сводится к задаче о правильном многограннике, вписанном в сферу. Имея такой многогранник, точки на сфере, соответствующие его вершинам, можно соединить геодезическими линиями (окружности максимального радиуса). Тогда сфера будет покрыта правильными криволинейными многоугольниками равной площади. Согласно теореме Эйлера существует только пять правильных многогранников, которые можно вписать в сферу. Из них наибольшим числом граней обладает икосаэдр (рис. 2.26, а). Таким образом, сфера может быть полностью покрыта только 20 одинаковыми криволинейными треугольниками (с равными сторонами и углами), чего недостаточно для анализа статистических свойств получаемых распределений.

156

В пакете «Mathematica» заложена полная информация о большом количестве геометрических тел, к которой можно получить доступ с помощью функции “PolyhedronData[]”. В частности, для изображения икосаэдра

“PolyhedronData["Icosahedron"]”.

Для исследования статистических свойств распределений, приведенных на рис. 2.25, икосаэдр можно случайным образом поворачивать относительно сферы и при каждом его расположении определять число точек, попадающих на каждый криволинейный треугольник (рис. 2.26, б).

Для этого сформируем список vertexes координат вершин икосаэдра:

“vertexes = PolyhedronData["Icosahedron", "VertexCoordinates"]”.

Эти координаты представлены для икосаэдра с единичным ребром. Для того чтобы они соответствовали расположению вершин на единичной сфере, необходимо нормировать полученные наборы координат. Результат сохраним в списке nodes:

“nodes = N[ #/ #.# ] & /@ vertexes;”.

Команда “PolyhedronData["Icosahedron", "Faces"]” возвращает спи-

сок, состоящий из двух частей. Первая часть содержит список вершин, а вторая имеет структуру “Polygon[faces]”, где список faces состоит из троек натуральных чисел, каждая из которых хранит номера вершин (из первого списка), образующих ту или иную грань. Длина списка faces равна 20. Команда

“facesSets = PolyhedronData["Icosahedron", "Faces"][[2, 1]]”

сохраняет набор троек вершин граней в списке facesSets.

Для реализации случайного размещения вершин икосаэдра на сфере зафиксируем некоторую точку (полюс), относительно радиус-вектора которой будем задавать случайные повороты вписанного в сферу икосаэдра:

“pole = (sinφ=Random[Real, {–1, 1}]; θ = Random[Real, {0, 2π }]; r=1;

r{Cos[θ] 1 − sinφ2 ], Sin[θ] 1 − sinφ2 ], sinφ}) ”.

Повернем каждую вершину икосаэдра на сфере на случайный угол u вокруг оси выбранного случайного полюса pole и сохраним изменения в том же списке:

157

“nodes = (RotationMatrix[u, pole].#) &/@ nodes) /. u Random[Real, {0, 2π }];”.

Изобразим вершины полученного случайно развернутого икосаэдра на единичной сфере красными точками:

“mainPointsPlot=Show[Graphics3D[{PointSize[Large], Red,Point[#]}& /@ nodes],

Graphics3D[{Opacity[0.3], Sphere[{0, 0, 0}, r]}], Axes → True,

Ticks → False, AxesLabel → {"X1", "X2", "X3"}]”,

где функция “Point[]” рисует точку с заданными координатами, функция “Sphere[]” дает изображение сферы заданного радиуса r (в примере r =1) с центром в заданной точке, функция “ PointSize[]” определяет размер точки при рисовании, “ Opacity[]” задает прозрачность изображаемой поверхности.

Создадим далее список pointsInFace из 20 пустых списков {}, соответствующих граням икосаэдра, в каждом из которых будем хранить число точек из исследуемого распределения, попавших в соответствующий правильный криволинейный треугольник с полученными выше вершинами nodes и заполним его, перебирая для каждой грани все имеющиеся на сфере точки распределения. Для подсчета будем принимать, что если максимальное из трех расстояний от рассматриваемой точки до вершин фиксированного треугольника не превышает расстояния между вершинами треугольника (в данном примере это расстояние равно 1.05146 – вычислить самостоятельно), то точка принадлежит треугольнику:

“pointsInFace = Table[{},{i,20}]; s = 1.05146;

Do[If[Max[ (positions[[ j]] − #).(positions[[ j]] − #) &/@nodes[[facesSets[[i]]

]]] ≤s,

pointsInFace[[i]]=Append[pointsInFace[[i]], positions[[j]] ] ], {i,20}, {j, Length[positions]}]; ”.

Изобразим на одном рисунке (рис. 2.26, б) полупрозрачную сферу с вершинами треугольников, точки распределения и те из них, которые попали в некоторый выбранный треугольник (например, с номером 5, но в силу использования случайных чисел при каждой реализации треугольник с этим номером будет по-разному размещаться на сфере).

158

“oneFacePlot = Show[Graphics3D[{PointSize[Large], Blue, Point[#]}& /@ nodes[[facesSets[[5]] ]] ] ];

pointsInFacePlot = Graphics3D[{PointSize[Large], Orange, Point[#]}& /@ pointsInFace[[5]] ];

Show[randomPointsPlot, mainPointsPlot, oneFacePlot, pointsInFacePlot]”.

Красные точки на рис. 2.26, б показывают положение вершин икосаэдра на сфере, синие точки – вершины выделенного правильного криволинейного треугольника, оранжевые – распределенные по сфере точки, попавшие в выбранный треугольник. Далее необходимо получить достаточную статистику попадания точек в треугольник, анализируя которую можно судить о характере распределения точек на сфере.

Многократно повторяя в цикле построенную процедуру и сохраняя в списке distributionList число точек на каждом из 20 треугольников при каждом их случайном размещении на сфере

“distributionList = Join[distributionList, Length /@ pointsInFace]”,

получим статистику попадания точек на сфере в правильные криволинейные треугольники, полностью покрывающие сферу.

Рис. 2.26. Разметка сферы вершинами икосаэдра:

а– икосаэдр; б – сфера, покрытая точками 2-го распределения

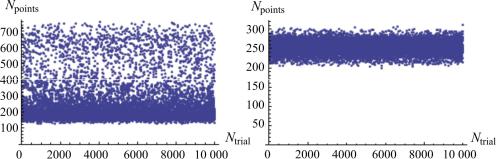
Врезультате для приведенных на рис. 2.25 распределений 5000 точек на сфере получена статистика их попаданий в различные треугольники (рис. 2.27). При равномерном распределении в каждый из 20 треугольников должно попадать примерно 250 точек.

159