
1465
.pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Пермский национальный исследовательский политехнический университет»
И.Ю. Зубко, Н.Д. Няшина
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ: ДИСКРЕТНЫЕ ПОДХОДЫ И ЧИСЛЕННЫЕ МЕТОДЫ
Утверждено Редакционно-издательским советом университета
в качестве учебного пособия
Издательство Пермского национального исследовательского
политехнического университета
2012
УДК 539.3 З-91
Рецензенты:
д-р физ.-мат. наук, профессор А.А. Роговой (Институт механики сплошных сред УрО РАН, г. Пермь);
д-р техн. наук, профессор В.Н. Аптуков (Пермский государственный национальный исследовательский университет)
Зубко, И.Ю.
З-91 Математическое моделирование: дискретные подходы и численные методы : учеб. пособие / И.Ю. Зубко, Н.Д. Няшина. – Пермь : Изд-воПерм. нац. исслед. политехн. ун-та, 2012. – 365 с.
ISBN 978-5-398-00947-7
В учебном пособии на примерах исследования физико-механических свойств кристаллических материалов (образцы с ОЦК-, ГЦК-, ГПУ-решетками, графит, графен) продемонстрированы возможности и обоснованы границы применимости как физического дискретного подхода, так и математического дискретного подхода. Достоинства и недостатки первого иллюстрируются на примере атомистических методов исследования термомеханических свойств кристаллических твердых тел и на примере метода клеточных автоматов. Особенности второго подхода демонстрируются на примерах численных методов решения уравнений механики сплошных сред – методе конечных элементов, методах решения обратных и некорректных задач.
Приводятся задания для самостоятельного выполнения и вопросы для самопроверки.
Изучение материала, включенного в учебное пособие, предусмотрено в 10–11 семестрах учебного плана профиля магистратуры «Математическое моделирование физико-механических процессов» по направлению 010400.68 Прикладная математика и информатика.
УДК 539.3
ISBN 978-5-398-00947-7 |
© ПНИПУ, 2012 |
ОГЛАВЛЕНИЕ
Введение...................................................................................................................................... |
5 |
Глава 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА |
|
И МЕХАНИКИ СПЛОШНОЙ СРЕДЫ............................................................................. |
8 |
1.1. Основы векторной и тензорной алгебры................................................................. |
8 |
1.2. Основные сведения из механики............................................................................ |
23 |
1.3. Балансовые уравнения и законы механики сплошных сред.............................. |
32 |
1.3.1. Основные соотношения кинематики сплошной среды............................ |
32 |
1.3.2. Основные соотношения динамики сплошной среды ................................ |
41 |
1.4. Практическое введение в пакет «Mathematica» .................................................... |
65 |
Список литературы к главе 1 ......................................................................................... |
95 |
Глава 2. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПОВЕДЕНИЯ |
|
ДЕФОРМИРУЕМЫХ ТВЕРДЫХ ТЕЛ НА АТОМАРНОМ УРОВНЕ. |
|
ДИСКРЕТНЫЙ ПОДХОД................................................................................................... |
97 |
2.1. История дискретного подхода. Метод молекулярной динамики. |
|
Сравнение различных потенциалов. Численные методы................................... |
98 |
2.2. Метод атомарной статики. Определение упругих модулей материалов |
|
с различной кристаллической решеткой................................................................ |
114 |
2.3. Учет температуры. Зависимость механических свойств |
|
конденсированных сред от температуры ............................................................ |
152 |
Список литературы к главе 2 ....................................................................................... |
165 |
Глава 3. МЕТОД КЛЕТОЧНЫХ АВТОМАТОВ........................................................ |
167 |
3.1. Моделирование с использованием имитационного подхода........................... |
167 |
3.2. Метод клеточных автоматов. Основные определения.......................................... |
174 |
3.3. Применение клеточных автоматов к описанию формирования |
|
дислокационной микроструктуры в металле ....................................................... |
179 |
Список литературы к главе 3 ....................................................................................... |
195 |
Глава 4. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ........................................................... |
197 |
4.1. Проекционный и вариационный подходы к построению разрешающих |
|
соотношений МКЭ................................................................................................. |
198 |
4.1.1. Проекционные методы. Основные понятия. ............................................ |
198 |
4.1.2. Вариационные принципы........................................................................... |
200 |
4.2. Виды конечных элементов и их классификация................................................ |
205 |
4.2.1. Одномерные пробные функции................................................................. |
208 |
4.2.2. Двумерные базисные функции высших степеней ................................... |
213 |
3
4.2.3. Трехмерные базисные функции................................................................. |
228 |
4.2.4. Разбиение области на элементы. Требования к конечным |
|
элементам..................................................................................................... |
230 |
4.3. Отображение и численное интегрирование........................................................ |
240 |
4.3.1. Параметрическое отображение.................................................................. |
240 |
4.3.2. Субпараметрические, изопараметрические |
|
и суперпараметрические элементы ........................................................... |
244 |
4.3.3. Численное интегрирование........................................................................ |
245 |
4.4. Разрешающие соотношения МКЭ для квазистатических задач теории |
|
упругости................................................................................................................ |
254 |
4.5. Постановка нестационарных и динамических задач........................................... |
260 |
4.5.1. Разрешающие соотношения МКЭ для пространственной |
|
конечно-элементной дискретизации......................................................... |
261 |
4.5.2. Разрешающие соотношения МКЭ для пространственной |
|
и временной конечно-элементной аппроксимации.................................... |
267 |
4.6. Физически нелинейные задачи. Пластичность, ползучесть............................. |
272 |
4.6.1. Метод переменных параметров упругости............................................... |
273 |
4.6.2. Методы начальных (дополнительных) напряжений................................ |
282 |
4.6.3. Методы начальных (дополнительных) деформаций................................. |
283 |
4.6.4. Метод Ньютона для решения нелинейной системы уравнений, |
|
полученной для физически нелинейной задачи....................................... |
288 |
4.7. Геометрически нелинейные задачи ..................................................................... |
291 |
4.7.1. Общие положения....................................................................................... |
291 |
4.7.2. Общий случай больших деформаций и напряжений............................... |
294 |
Выводы по главе 4 ....................................................................................................... |
298 |
Список литературы к главе 4 ....................................................................................... |
300 |
Глава 5. ОБРАТНЫЕ И НЕКОРРЕКТНЫЕ ЗАДАЧИ.............................................. |
301 |
5.1. Основные понятия и примеры.............................................................................. |
301 |
5.1.1. Обратные и некорректные задачи............................................................. |
302 |
5.1.2. Понятие условно корректной задачи ........................................................ |
307 |
5.2. Способы преодоления некорректности. Методы регуляризации..................... |
313 |
5.2.1. Метод квазирешений.................................................................................. |
313 |
5.2.2. Метод регуляризации Тихонова................................................................ |
315 |
5.2.3. Метод регуляризации на компактных множествах................................. |
325 |
5.2.4. Итерационные методы решения некорректных задач............................. |
327 |
5.2.5. Метод усеченных сингулярных разложений............................................ |
333 |
5.2.6. Проекционный метод.................................................................................. |
335 |
5.3. Некоторые примеры решения обратных задач................................................... |
337 |
5.3.1. Обратные ретроспективные задачи........................................................... |
337 |
5.3.2. Коэффициентные обратные задачи в механике деформируемого |
|
твердого тела................................................................................................ |
355 |
Список литературы к главе 5 ....................................................................................... |
364 |
4
ВВЕДЕНИЕ
В математическом моделировании физико-механических систем, начиная с первых исследований простейших упругих реакций деформируемых тел, сосуществовали два подхода к теоретическому исследованию природы – дискретный (молекулярная теория Навье, Коши, Пуассона, 1827 год) и непрерывный (теория потенциала Грина, 1838 год). Эти подходы в чем-то противостоят один другому, а в чем-то дополняют друг друга. Оба подхода имеют свои преимущества, недостатки и границы применимости. Если обратить внимание на окружающие нас объекты, то многие из них в явной форме демонстрируют свое дискретное строение – кирпичная кладка стен домов, поликристаллическая структура на изломе образца металла, осколки керамики, композиционные материалы. Для многих других объектов дискретное строение становится заметным лишь при исследовании под микроскопом. Части, из которых состоят перечисленные тела, также могут иметь более мелкую дискретную структуру. Причем современная физика не дает никаких оснований утверждать, что существуют наименьшие частицы, которые бы, организуясь некоторым образом, формировали бы все многообразие окружающего нас мира. Поэтому применяя к моделированию физико-механического поведения природных и искусственных объектов дискретный подход, основанный на детальном описании совместного движения и взаимодействия составных частей изучаемых объектов, надо всегда вводить ограничения в виде предположений относительно принимаемой неделимости этих частей, заменяя влияние их реальной структуры некоторыми гипотезами или моделями. Другим важным ограничением дискретного подхода является практическая невозможность в большинстве случаев описать поведение моделируемого объекта, рассматривая все множество его частей, принятых за неделимые. Например, крайне сложно описать процессы деформирования и разрушения многоэтажного строения, под которым происходит проседание грунта, на уровне отдельных кирпичей, вводя в модель все кирпичи этого строения. Крайне сложно описать деформацию лопатки работающего авиационного двигателя, пытаясь учесть движение и взаимодействие всех атомов этой лопатки. Разумеется, современные достижения в развитии многопроцессорной вычислительной техники и производительных алгоритмов позволяют проводить исследования объектов,
5

состоящих из очень большого числа дискретных частей, но все же моделировать сложные физико-механические процессы в неоднородном теле, размеры которого на порядки превышают размеры выбранных элементарных составляющих, невозможно. Здесь более плодотворным оказывается непрерывный подход, для применения которого характеристики большого числа отдельных элементов «размазывают» по объему, занимаемому телом, и переходят к так называемым континуальным полям свойств и уравнениям, формулировкой которых занимается механика и физика сплошных сред. Дискретный подход при этом переходе нельзя считать бесполезным – он дает возможность установить закономерности поведения и реакции на прикладываемые воздействия представительного объема среды, состоящего из сравнительно небольшого числа структурных элементов. Эти реакции позволяют уточнить определяющие соотношения среды, которые можно использовать в континуальных моделях. Дискретный подход в этом случае его применения можно назвать физическим.
Полученные уравнения для континуума являются дифференциальными уравнениями в частных производных и их аналитическое решение, в особенности для тел сложной формы, может быть получено только в очень редких случаях для простых видов нагружения и закрепления. Для получения оценок заданной точности решений этих уравнений применяют теорию численных методов, в основе которой лежит способ дискретизации полевых уравнений. В этом смысле мы имеем дело с проявлением другой грани дискретного подхода, которую можно назвать математической. В последние годы появляются работы, в которых стыкуется физическая и математическая стороны дискретного подхода, когда численные методы решения задач МСС совмещаются с подходом молекулярной динамики в окрестностях различных особенностей. К ним относятся области носа трещины, ядра дислокации, межфазной границы, некоторых контактных границ – зоны, где решения уравнений, полученных в рамках классического подхода МСС, имеют сингулярности и бывает достаточно сложно обеспечить сходимость численных методов. При этом решаются непростые задачи объединения дискретного и континуального способов описания природы1.
Цель предлагаемого пособия – продемонстрировать ряд возможностей и указать границы применимости как физического дискретного подхода, так и математического. Достоинства и недостатки первого подхода обсуждаются на примере атомистического подхода к исследованию
1 Рippan R., Gumbsch P. Multiscale modelling of plasticity and fracture by means of dislocation mechanics // CISM. Courses and lectures. Springer Wien New York, 2010. No. 522. 394 p.
6

свойств кристаллических твердых тел – методах молекулярной динамики
истатики, а также на примере метода клеточных автоматов, с помощью которого моделируются процессы, идущие на более высоком масштабном уровне – уровне дислокаций. Второй подход демонстрируется на примерах использования метода конечных элементов, методов решения обратных и некорректных задач механики сплошных сред.
Учебное пособие предназначено для магистрантов, обучающихся по направлению подготовки 010400.68 «Прикладная математика и информатика». Поскольку не все бакалавры, поступающие в магистратуру по указанному направлению, изучали полновесные курсы тензорного анализа
имеханики сплошной среды, пособие содержит краткую вводную часть, очерчивающую круг понятий этих дисциплин, необходимых для лучшего восприятия излагаемого в пособии материала.
Пособие также содержит задания, предлагаемые для самостоятельного выполнения, которые призваны инициировать интерес к выполнению научных исследований в освещаемой области знаний, а также помочь освоить аппарат физических и математических дискретных методов для применения к решению задач, возникающих в собственной научной работе магистрантов.
Вкачестве руководства по изучению основных принципов и методологии математического моделирования рекомендуется учебное пособие под редакцией П.В. Трусова2.
Авторы выражают признательность профессору П.В. Трусову за ценные предложения и замечания, высказанные при обсуждении пособия.
2 Введение в математическое моделирование / В.Н. Ашихмин [и др.]; под ред. П.В. Трусова.
М.: Логос, 2005. 440 с.
7
ГЛАВА 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕНЗОРНОГО АНАЛИЗА И МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
Для достижения замкнутости изложения материала в п. 1.1. кратко обсудим основы математического аппарата (тензорной алгебры), необходимого для изучения последующих разделов. При этом будем выделять векторы и тензоры жирным шрифтом. Векторы будем обозначать малыми латинскими буквами a, b, x, y и так далее, а тензоры – как правило, заглавными, например A, B, T, R, скалярные величины будут обозначаться обычным шрифтом, например, α , β , i, k. В п. 1.2 и 1.3 приводятся основные сведения из механики. Основной задачей изложения материала п. 1.3 является представление уравнений механики сплошных сред (МСС), термодинамики и получение уравнений диффузии в растворе двух и более компонент. В последующих главах при моделировании механического и теплового поведения дискретных систем осредненные результаты расчетов будут сравниваться с решениями соответствующих уравнений МСС для непрерывных систем, приведенных в п. 1.3, в гл. 4 и 5 будут рассмотрены специальные разделы теории численных методов для решения уравнений из п. 1.3 при различных граничных условиях. П. 1.4 посвящен практическому введению в вычислительную систему «Mathematica» разработчика Wolfram Research, которую предлагается использовать в качестве инструмента при освоении материала последующих глав.
1.1. ОСНОВЫ ВЕКТОРНОЙ И ТЕНЗОРНОЙ АЛГЕБРЫ
После открытия человеком в далеком прошлом понятия числа появились арифметические действия, и помимо натурального ряда чисел появились отрицательные, рациональные, действительные, комплексные числа. Но и этого оказалось мало. Новый качественный прорыв был совершен совсем в другом направлении [1]. И этот путь можно повторить, ответив на вопрос: а что, если начать все не с натуральных чисел, а с чего-то другого? Но при этом становится не совсем понятно, что будут собой представлять сложение и умножение. Примем, что это будут операции, удовлетворяющие знакомым свойствам типа (a + b)c = ac + bc . На основе этого возник-
ла, так называемая, абстрактная алгебра. А ее самым ярким и важным в свое время примером стало векторное исчисление.
8
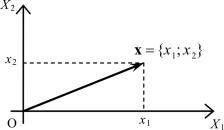
Рис. 1.1. Представление вектора
спомощью направленного отрезка
иего координат
Новые объекты – векторы – характеризовались уже не одним только числом (длиной или модулем), но и принципиально новым понятием – направлением. Хотя, используя компонентную запись
об
вектора ( x ={x1; x2 } в двумерном пространстве, например на плоско-
об
сти (рис. 1.1), или x ={x1; x2 ; x3}
в трехмерном пространстве), можно убедиться, что и задание направления напрямую связано с числами, а точнее – с объединением двух (в двумерном случае) или трех (в трехмерном случае) чисел.
А новое свойство (направление) возникает именно оттого, что числа стали рассматриваться не только по отдельности, но и как не-
разделимые |
упорядоченные пары ({x1; x2} ≠ {x2 ; x1} ) или тройки |
({x1; x2 ; x3} ≠ |
{x2 ; x3 ; x1} ). Заметим, что переход от вектора к его компо- |
нентам требует введения системы координат и соответствующих векторов базиса (здесь и далее, если не оговорено иное, используется декартова ортогональная система координат с ортонормированным базисом). Такой переход и стал основой очередного качественного скачка в мышлении человека. Причем известны и «родитель» векторов, и время их рождения – понятие вектора впервые было явно введено Саймоном Стевином (S. Stevin) примерно в 1580 году для описания понятия силы и доказательства правила сложения сил (известного сейчас как «правило треугольника»).
Вспомним основные свойства векторов и действия над ними. Векторы, как направленные отрезки, складываются по правилу треугольника (или па-
раллелограмма), что в координатной записи x = {x1; x2 ; x3}, |
y = {y1; y2 ; y3} |
||||||||
приводит к обычному покоординатному сложению: |
|
||||||||
x + y = {x1 + y1; x2 + y2 ; x3 + y3} . |
(1.1) |
||||||||
Вариантов умножения существует уже два. Скалярное умножение |
|||||||||
есть число |
|
||||||||
x y = y x = |
|
x |
|
|
|
y |
|
cos α, |
(1.2) |
|
|
|
|
||||||
9

равное произведению длин векторов на косинус угла α между ними, которое в координатной форме записывается как
x y = x1 y1 + x2 y2 + x3 y3 . |
(1.2') |
С помощью скалярного умножения находится так называемая проекция ab одного вектора а на прямую, вдоль которой направлен другой век-
тор b: a = |
a b |
= |
b a |
. При этом часто говорят просто о проекции вектора а |
||||
|
|
|||||||
b |
b |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
на вектор b. Если рассматривается проекция ae вектора а на единичный
вектор e (его длина e =1, то есть e e =1), то ae = a e = e a .
Второй вариант умножения – это векторное умножение, результатом которого является вектор
z = x × y ,
причем длина вектора z
z |
|
= |
|
x |
|
|
|
y |
|
sin α , |
(1.3) |
|
|
|
|
|
то есть площади параллелограмма, построенного на векторах x и y, как на сторонах, а направление z определяется по «правилу буравчика» перпендикулярно обоим векторам (рис. 1.2) – поворот от вектора x к вектору y с конца полученного вектора z видится как происходящий против часовой стрелки. При перестановке сомножителей в векторном произведении направление вектора z меняется на противоположное, и поворот от вектора x к вектору y будет представляться происходящим по часовой стрелке. В координатной форме результат векторного умножения имеет более сложный вид:
x × y= {x2 y3− x3 y2; x3 y1− x1 y3; x1 y2− x2 y1}. |
(1.3') |
Отметим, что результат векторного умножения данного вектора x на единичный вектор e, перпендикулярный x, можно представлять как поворот вектора x на угол 90° вокруг оси, задаваемой вектором e (представить это можно, заменив на рис. 1.2 вектор y на вектор e при α = 90° ). Длина нового вектора совпадает с длиной x согласно (1.3). При векторном перемножении взаимно ортогональных единичных базисных векторов, например, обозначенных как i, j, k, получим
i × j= k, j× k= i, k× =i j,× i =k− j.
10
