
1004
.pdf
Интегрируя уравнение (7.30), представим его в виде
pxy = dP h |
y ± y0 |
. |
(7.31) |
||
h |
|||||
dx |
|
|
|
||
Полученное решение показывает, что в рамках оговоренных приближений распределение напряжений сдвига в зазоре линейно. Константа y0 по своему физическому смыслу – это координата сечения, в котором напряжения сдвига равны нулю. Из условия симметрии следует, что при отсутствии фрикции (U1/U2) y0 = 0. Поэтому все уравнения симметричного вальцевания существенно упрощаются. В случае несимметричного вальцевания сечение нулевых напряжений сдвига смещается в сторону валка, вращающегося с большей окружной скоростью.
Каландрование – процесс непрерывного продавливания (прокатка) полимерного материала через зазор между вращающимися навстречу друг другу обогреваемыми полыми цилиндрами, при котором образуется бесконечный тонкий лист или пленка. В отличие от вальцевания при каландровании полимерный расплав проходит через каждый зазор только один раз. Каландрование широко применяется в резиновой промышленности и индустрии переработки пластмасс для изготовления тонких пленок и листов, а также для наложения полимерного слоя на ткань (рис. 7.10, где обозначено: 1 – смеситель закрытого типа; 2 – вальцы; 3 – детектор металла; 4 – Z-образный каландр; 5 – охлаждающие барабаны; 6 – толщиномер; 7 – устройство для обрезания кромок; 8 – закаточное устройство).
Рис. 7.10
101
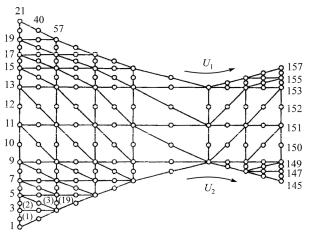
Рис. 7.11
Анализ процесса каландрования методом конечных элементов (МКЭ) был осуществлен Влачопулосом. Область течения полимерного материала в зазоре валков разбивалась на треугольные элементы (рис. 7.11), а численное интегрирование системы исходных дифференциальных уравнений проводилось методом «взвешенных невязок» (разновидность метода Галеркина). Полимерный расплав рассматривался как жидкость с постоянной (эффективной) вязкостью.
7.5. Анализ методов формования методом конечных элементов
Исходными дифференциальными выражениями являются уравнение сохранения количества движения
∂P / ∂x = ∂τxy / ∂y |
(7.32) |
и уравнение неразрывности
∂(hvx )/ ∂x = 0, |
(7.33) |
где h – половина зазора между валками.
102
Цель решения – определение узловых значений скоростей и давлений. В качестве аппроксимирующих функций для поля скоростей использовались параболические функции, а для поля давлений – линейные.
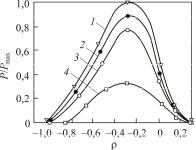
На рис. 7.12 показан результат анализа методом конечных элемен-
тов каландрования полимерной Рис. 7.12 композиции с n = 0,25 (течение по
реологическому закону Освальда де Виля для полимерных систем).
Причем R = 10 см; 2H0 = 0,01 см; m = 0,1 Н·с/см2; Pmax = 0,32 МПа. На рис. 7.12 обозначено: 1 – U1 = U2 = 40 см/с; 2 – U1 – U2 = 30 см/c;
3 – U1 – U2 = 20 см/с; 4 – U1 = 20 см /с, U2 = 40 см/с.
При анализе неизотермического каландрования уравнение сохранения энергии составляют, предполагая, что теплофизические характеристики полимерного материала имеют постоянное значение. Поэтому в рамках смазочной аппроксимации искомое дифференциальное уравнение принимает вид
ρC |
|
v |
∂T |
= K |
∂2T |
+τ |
∂vx . |
(7.34) |
|
p |
|
x ∂x |
|
∂x2 |
|
yx ∂y |
|
Интегрирование этого уравнения осуществляется одновременно с интегрированием уравнений (7.32) и (7.33). Граничное условие – постоянство температуры полимерного материала на входе, которая принимается равной температуре поверхности валков. Решение уравнения (7.34) было получено методом конечных разностей, причем значения vx и dvx/dy определялись методом конечных элементов. Зависимости перепада (∆Т) максимальной температуры полимерного расплава от продольной координаты ρ при различных значениях n приведены на рис. 7.13. Расчет проводился для каландра: R = 15 см;
Н0 = 0,025 см; U = 30 см/с; λ = 0,48; ρ = 1 г/см3; Cp = 2,11 Дж/(г·К); k = 1,7·10–3 Дж/(см·с·К).
103

Представляет интерес наличие двух температурных максимумов на приведенных кривых. Появление этих экстремальных температур – следствие взаимного наложения диссипативного разогрева (определяемого распределением скоростей сдвига) и теплопередачи к поверхности валков.
Примечательно, что температура выхода практически не отражает высокой температуры, до которой разогревается
проходящий через зазор полимерный материал. Эта температура очень зависит от реологического параметра n.
Влачопулос предположил, что величиной и распределением температурных максимумов можно объяснить возможное появление пузырей в каландрованных листах. Такие воздушные пузыри иногда появляются на небольшом расстоянии от поверхности каландрованных листов, например, из полимерного материала – поливинилхлорида.
7.6. Литье термопластов под давлением
Литье термопластов под давлением разделяется на два процесса. Первый включает в себя плавление, перемешивание, сжатие и течение расплава полимерного материала, осуществляемые в пластификаторе литьевой машины, в второй – собственно изготовление изделия в полости формы или пресс-формы. Большинство литьевых машин снабжено червячными пластификаторами с осевым перемещением витков шнека (червяка) и имеет горизонтальную компоновку. На рис. 7.14, a представлена литьевая машина с плунжерным пластификатором (1 – форма; 2 – цилиндр; 3 – бункер; 4 – плунжер; 5 – торпеда); на рис. 7.14, б – литьевая машина с червячным пластификатором осевого перемещения; на рис. 7.14, в – конструкция типичного шнек-винтового (червячного) пластификатора.
104
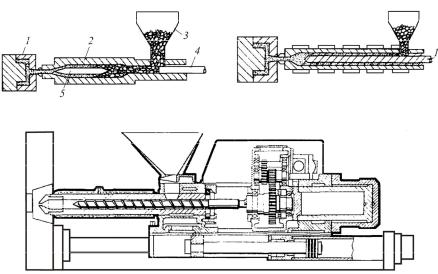
а |
б |
в
Рис. 7.14
Рассмотрим математическое моделирование заполнения формы для изделия в виде декоративного диска для автомобильного колеса с впуском, расположенным в центре по отношению к изделию. На рис. 7.15 показано поперечное сечение дисковидной литьевой пресс-формы с впуском в центре диска (схематически изображены застывший пристенный слой, образующийся в процессе заполнения формы, и клиновидный профиль скоростей течения): 1 – вход в форму с температурой расплава Т1; 2 – «непрерывное» изотермическое течение в подводящей трубе; 3 – фронт потока полимера; 4 – внутренняя стенка формы с температурой Т0; 5 – область смешения; 6 – застывший пристенный слой полимерного материала.
В процессе изготовления изделия в форме иногда может образовываться пристенный (пограничный) слой застывшего материала (застеклованного термопласта), что вызовет уменьшение сечения канала и соответствующее увеличение сопротивления в потоке полимерной композиции.
105
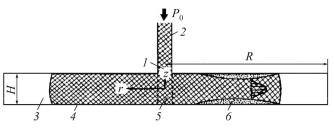
Рис. 7.15
Предположим, что теплофизические свойства полимерного расплава постоянны, состояние его потока – квазистационарное – dvr / dt = 0. При этом составляющие тензора касательных напряже-
ний (в сферических координатах) τrr и τθθ в уравнении сохранения r-момента от приложенного касательного напряжения пренебрежимо малы, как и осевая теплопередача в уравнении сохранения энергии. Тогда выражения для механического равновесия при течении полимерного композиционного материала и его энергетического баланса имеют вид:
|
|
|
dτzr |
= − dP |
; |
|
|
(7.35) |
|||
|
|
|
dz |
|
|
dr |
|
|
|
|
|
∂T |
+vr |
∂T |
= k |
∂2T |
|
v |
∂v |
(7.36) |
|||
ρCp |
∂t |
|
∂z |
2 −τθθ |
r −τzr |
r . |
|||||
|
|
∂r |
|
|
|
|
r |
∂z |
|
||
Выражение τθθ (vr / r ) значимо только при малых величинах r.
Используя в качестве реологического уравнения степенной закон Освальда де Виля, получим
τzp = −m |
|
dv |
|
n−1 dv |
(7.37) |
|
|
||||
|
r |
|
r , |
||
|
|
dz |
|
dz |
|
где m = mo exp[∆E / RT ]; n − константа течения конкретного материала.
106
Радиальный перепад давления определяется по формуле Бергера
и Гогоса:
|
|
|
|
|
|
|
|
dP |
|
|
|
Qt |
|
|
|
= |
|
|
|
, |
(7.38) |
||
dz |
|
|
|
||||
|
|
H / 2 |
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
4πr |
|
(z1+s / ms )dz. |
|
|
|
|
|
|
0 |
|
|
|
|
где s =1/ n; H − толщина диска; Q – объемный расход полимерного материала; t – время заполнения пресс-формы.
Интегрируя дифференциальное уравнение (7.15) и используя выражение (7.38), можно получить уравнение для определения скорости потока:
|
dP |
|
s |
x |
z s |
|
||
|
|
|
||||||
vr (r, z, t) = − |
|
|
|
∫ |
|
|
dz. |
(7.39) |
dr |
|
|
m |
|||||
|
|
|
|
H /2 |
|
|
|
|
При численных методах определения перепада давления и профиля скоростей течения полимерного потока в пресс-форме необходимо использовать метод итерации, повторяя расчет давления в каждом радиальном положении до тех пор, пока объемный расход полимерного расплава в полости пресс-формы не станет таким же, как
иво впуске.
Вуравнениях (7.38) и (7.39) коэффициент консистенции (m) применительно к необогреваемой технологической оснастке не остается постоянным в направлении z, поскольку в этом же направлении (по глубине формы) уменьшается температура. Поэтому скорость полимерного потока постоянна лишь на ранней стадии заполнения формы, а затем она снижается.
На рис. 7.16 представлены соответствующие зависимости времени заполнения формы от температуры полимерного расплава на входе в оснастку и от давления впрыска для поливинилхлорида. Раз-
меры полости пресс-формы: R = 9 см, H = 0,635 см. Реологические характеристики ПВХ: n = 0,5; m = 4·104 Па·с; А = 6,45·10–8; ∆Е =
= 116,2 кДж/(г·моль); ρ = 1,3·103 кг/м3; Ср = 1,88 кДж/(кг·К); k =
107

= 9,6·10–2 Дж/(м·с·К). Значения Т1, °С: 1 – 202, 2 – 205, 3 – 210; значе-
ния Р0, МПа: 4 – 42, 5 – 52,5, 6 – 70 (см. рис. 7.16).
Угловой коэффициент касательной к кривой «время заполнения – температура расплава полимера» зависит от энергии активации вязкого течения, т.е. от температурной чувствительности коэффициента консистенции m.
Угловой коэффициент касательной к кривой «время заполнения – давление впрыска» зависит от индекса течения (n), увеличиваясь с уменьшением последнего.
На рис. 7.17 показано распределение температуры при заполнении той же пресс-формы расплавом поливинилхлорида, имеющим на входе температуру 202 °С. Давление впрыска составляло 105 МПа.
Z = 2r / H; H = 0,635 см; t = 1,45 c; R = 9 см; T1 = 202 °C; T0 = 30 °С. Числа у кривых – значения Z .
Видно, что на расстоянии, равном |
|
|
половине пути до стенки, течение носит |
|
|
изотермический характер. Это объясня- |
|
|
ется тем, что профиль скоростей в этом |
|
|
слое потока почти плоский и теплопере- |
|
|
дача ничтожна. Только вблизи стенки |
|
|
полости формы происходит быстрое и |
|
|
значительное охлаждение расплава за |
|
|
счет теплопередачи материалу оснастки. |
|
|
При температуре 150 °С, когда ПВХ |
Рис. 7.17 |
|
имеет практически бесконечный дина- |
||
|
||
108 |
|
мический коэффициент вязкости, на расстоянии r > 2,5 см уже образуется тонкий пограничный слой затвердевшего полимера. При меньших значениях давления впрыска образуется, естественно, более толстый слой застеклованного полимера.
Наоборот, увеличение давления впрыска, температуры расплава и температуры пресс-формы (технологической оснастки), а также глубины полости формы приводит к уменьшению толщины пристенного слоя изделия из полимерного материала. Профиль застывшего или застеклованного слоя, в зависимости от термомеханической кривой полимерного материала, характеризуется наличием максимума («горба») (см. рис. 7.17). Вблизи зоны впуска за счет свежих порций горячего расплава толщина этого слоя сохраняется минимальной. На участке развития фронта расплав, находящийся вблизи стенок оснастки, еще достаточно горяч, поскольку поток здесь формируется из центральных слоев. На участке «горба» течение останавливается, что и является причиной недолива при малых давлениях впрыска. Кроме того, наличие пристенного слоя затвердевшей полимерной композиции приводит к продольному растяжению расплава и появлению z-составляющей скорости, что особенно заметно в области входа в пресс-форму. Поэтому в полостях, имеющих форму диска, наличие продольного течения опровергает принятое выше допущение о возможности пренебрежения компонентой dvz / dr.
Итак, теоретические исследования технологии литья под давлением показывают, что общая картина течения и профиль фронта (скоростей слоев) потока полимерного материала слабо зависят от реологических свойств расплава: ньютоновские и псевдопластичные жидковязкие системы обнаруживают почти одинаковый характер развития фронта потока. Этот вывод подтвержден экспериментально при помощи скоростной фотосъемки процесса литья под давлением различных полимеров в прозрачную форму.
109
7.7. Переработка реакционно-активных полимерных композиций
Литье под давлением реакционно-активных олигомеров. Этот вид технологического процесса позволяет изготавливать изделия на основе линейных высокомолекулярных, разветвленных и пространственно сшитых полимеров (реактопластов). Два или более низкомолекулярных полимера (олигомера), имеющие концевые антиподные реакционно-активные группы предварительно смешивают и впрыскивают в пресс-форму необходимой конфигурации. В процессе заполнения формы и соответствующем нагреве происходит реакция полимеризации, которая может завершаться и после формования изделия. Подобная технология используется и при изготовлении различных по массе и геометрии зарядов ракетных двигателей на основе высоконаполненных полимерных связующих – смесевых твердых ракетных топлив. При этом их отверждение может длиться несколько суток.
Заполнение формы реакционно-активной полимерной компо-
зицией. Рассмотрим, например, очень длинную и очень широкую форму с малой глубиной, заполняемую при постоянной температуре смесью олигомерных молекул состава АА и ВВ. Оба типа молекул бифункциональны и их молекулярная масса равна Мо. Реакция полимеризации обратима, протекает по типу «голова к хвосту» в соответствии с идеализированной ступенчатой полимеризацией (поликонденсацией) без образования малых молекул:
k f , kr |
(7.40) |
AA + BB ← →AA − BB[−∆H ], |
здесь kf и kr – константы скоростей прямой и обратной реакций. Приняв молекулярную массу полимера (AA − BB)x равной Mx,
можно записать уравнение обратимой реакции |
поликонденсации |
в общем виде: |
|
k f , kr |
(7.41) |
M x + M y ← →M x+ y[−∆H ]. |
|
110 |
|
