неупругих деформациях поликристаллов // Вестник Тамбов.
ун-та. – 2016. – № 3. – С. 1338–1341.
5. Швейкин А.И., Ашихмин В.Н., Трусов П.В. О моделях ротации решетки при деформировании металлов // Вестник Пермского национального исследовательского политехнического универ-
ситета. Механика. – 2010. – №1. – С. 111–127.
ИССЛЕДОВАНИЕ БАЗАЛЬТОВЫХ ВОЛОКОН НА СТАДИИ ЗАКРИТИЧЕСКОГО ДЕФОРМИРОВАНИЯ В УСЛОВИЯХ КВАЗИСТАТИЧЕСКОГО НАГРУЖЕНИЯ
М.С. Темерова, В.Э. Вильдеман
Пермский национальный исследовательский политехнический университет,
Пермь, Россия, temerova@gmail.com,wildemann@pstu.ru
Рассматриваются экспериментальные исследования пучков базальтовых волокон на закритической стадии деформирования. Экспериментально исследовались пучки с количеством нитей n = 1, 2, 3 и 5. В работе получены диаграммы деформирования с четко выраженными участками вступления волокон в работу. Получены прочностные характеристики, которые характеризуются большимстатистическимразбросом.
Ключевые слова: закритическая стадия деформирования, испытание нарастяжение, экспериментальнаямеханика, базальтовоеволокно.
Закритическая стадия деформирования является одной из характерных особенностей нелинейного поведения материалов, связанного с накоплением структурных повреждений. Закономерности закритического деформирования необходимо знать при использовании деформационных резервов материала для повышения живучести и несущей способности конструкции. Каждая точка на ниспадающей ветви может соответствовать моменту потери несущей способности [1].
Работа посвящена исследованию пучков базальтовых волокон на закритической стадии деформирования. Экспериментально исследовались пучки с количеством нитей n = 1, 2, 3 и 5.
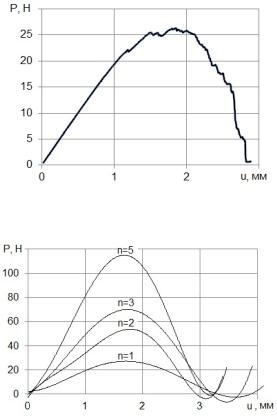
Из рис. 1, 2 видно, что волокна вступают в работу не одновременно, чтосвязаноспостепеннымразрушениемволокон.
Рис. 1. Типовая диаграмма деформирования пучка
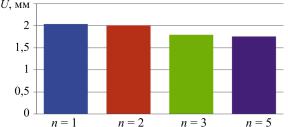
Рис. 2. Аппроксимации пучков, где n = 1, 2, 3 и 5 нитей
Волокна, имеющие самое низкое разрывное удлинение разрушаются в упругой зоне. Предел прочности достигается в интервале 45–60 % от удлинения волокна, происходит разрушение основной части волокон. Ниспадающая ветвь соответствует постепенному разрушению оставшихся волокон и вытягиванию уже разрушенных (рис. 3).
Рис. 3. Зависимость удлинения при максимальной нагрузке от числа нитей в пучке
Полученные прочностные характеристики волокон характеризуются большим статистическим разбросом, который необходимо учитывать при моделировании и изготовлении конструкционных и функциональных материалов из них.
Исследование выполнено за счет средств гранта Российского научного фонда (проект № 16-19-00069) в Пермском национальном исследовательском политехническом университете.
Список литературы
1.Вильдеман В.Э., Соколкин Ю.В., Ташкинов А.А. Механика неупругого деформирования и разрушения композиционных материалов / под ред. Ю.В. Соколкина. – М.: Наука: Физматлит, 1997. – 288 с.
2.Temerova M.S., Lobanov D.S. Features of quasistatic tests
of threads and fabrics // PNRPU Mechanics Bulletin. – 2013. –
№2. – С. 96–109.
3.Темерова М.С. Экспериментальное исследование армирующих элементов композиционных материалов // Математическое моделирование в естественных науках. 7–10 октября, 2015. –
С. 441–442.
4.Вильдеман В.Э., Соколкин Ю.В., Ташкинов А.А. Механика неупругого деформирования и разрушения композиционных материалов / под ред. Ю.В. Соколкина. – М.: Наука: Физ-
матлит, 1997. – 288 с.
383
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДЫХАТЕЛЬНОЙ СИСТЕМЫ ЧЕЛОВЕКА С УЧЕТОМ ЭВОЛЮЦИИ ФУНКЦИОНАЛЬНЫХ НАРУШЕНИЙ
П.В. Трусов1,2, М.Ю. Цинкер1,2
1Пермский национальный исследовательский политехнический университет,
Пермь, Россия, tpv@matmod.pstu.ac.ru,
2Федеральный научный центр медико-профилактических технологий управления рисками здоровью населения, Пермь, Россия, cinker@fcrisk.ru
Статья посвящена разработке математической модели «мезоуровня» дыхательной системы в рамках многоуровневой модели эволюции функциональных нарушений человека. Применение модели поможет в улучшении понимания механики процесса дыхания, механизмов накопления функциональных нарушений при ингаляционном поступлении химических веществ.
Ключевые слова: математическое моделирование, дыхательная система человека, эволюция функциональных нарушений, факторы среды обитания.
Коллективом авторов [1] разрабатывается многоуровневая математическая модель эволюции функциональных нарушений человеческого организма. В данной математической модели человеческий организм представлен набором органов и систем, взаимосвязанных между собой. Для описания функциональных нарушений органов было введено понятие «поврежденность» (D). Поврежденность каждого органа принимает значение в пределах интервала [0; 1], где0 соответствуетотсутствиюнарушений, а 1 – невозможности выполнять органом свои функции. Величина, равная 1− D, соответствует функциональности. Поврежденность и связанная с ней функциональность с течением времени изменяют свое значение. Механизмы функциональных нарушений связаны с естественными процессами (старение, восстановление организма) и действием факторовсредыобитанияиобразажизни[2].
В многоуровневой модели рассматриваются различные масштабные и структурные уровни. На макроуровне рассматриваются осредненные пространственно-временные характеристики
органов и систем (потоки веществ между органами) и используются интегральные параметры поврежденности, на мезоуровне подробно рассматриваются процессы, происходящие в отдельных органах и системах [3], в том числе в дыхательной системе [4]. На основе многоуровневой модели разработаны подходы к оценке риска здоровью населения [5].
Дыхание человека – совокупность процессов деформации легких, газовой динамики в системе каналов сложной формы и диффузии через биологическую мембрану. Полная математическая модель, описывающая процесс дыхания, является нелинейной, что обусловливает необходимость применения итерационной процедуры для описания этапов: «изменение формы легких – изменение давления в легких – изменение давления в бронхах – движение воздуха – газообмен (изменение уровня газов в крови) – изменение формы – …».
Движение воздуха по крупным воздухоносным путям, входящим в соответствующие участки легких, описывается уравнениями газовой динамики [6, 7]. Основные результаты моделирования течения воздуха в крупных воздухоносных путях приведены в [8].
Исследование движения воздуха в более мелких воздухоносных путях средствами газовой динамики затруднено ввиду сложной геометрии и большого числа параметров. В математической модели дыхательной системы легкие человека, заполненные более мелкими дыхательными путями и воздухом, содержащимся в них, представлены упругодеформируемой насыщенной газом пористой средой [9]. Насыщенная газом пористая среда представлена двухфазной сплошной средой, одна из фаз которой – деформируемый скелет среды, описываемый моделью деформируемого твердого тела [10]; вторая фаза – многокомпонентная смесь газов, заполняющая поровое пространство. В качестве определяющих соотношений для задачи движения воздуха через деформируемую пористую среду используется закон Гука в скоростной форме. В качестве граничных условий для задачи упругости используются граничные условия кинематического типа.
Применение разрабатываемой модели позволит оценивать поступление веществ из окружающей среды в кровеносную систему, имитировать негативное действие факторов среды обитания на организм человека и строить прогнозы функционального состояния дыхательной системы человека. Результаты проекта будут иметь как научное значение – улучшение понимания механики процесса дыхания, механизмов накопления функциональных нарушений при ингаляционном поступлении химических веществ с вдыхаемым воздухом, так и прикладное значение – оценка и прогноз индивидуального и популяционного риска для здоровья.
Список литературы
1. Математическая модель эволюции функциональных нарушений в организме человека с учетом внешнесредовых факторов / П.В. Трусов, Н.В. Зайцева, Д.А. Кирьянов, М.Р. Камалтдинов, М.Ю. Цинкер, В.М. Чигвинцев, Д.В. Ланин // Математическая биология и биоинформатика. – 2012. – Т. 7, № 2. –
С. 589–610. DOI: 10.17537/2012.7.589.
2. Камалтдинов М.Р., Цинкер М.Ю., Чигвинцев В.М. Моделирование рисков функциональных нарушений пищеварительной системы, обусловленное воздействием факторов образа жизни //
Санитарный врач. – 2013. – № 9. – С. 67–69.
3 Камалтдинов М.Р. Трехмерное моделирование моторики антродуоденальной области пищеварительного тракта для задач оценки риска здоровью при пероральной экспозиции химических веществ // Анализ риска здоровью. – 2014. – № 2. – С. 68–77.
4.Трусов П.В., Зайцева Н.В., Цинкер М.Ю. Моделирование процесса дыхания человека: концептуальная и математическая постановки // Математическая биология и биоинформати-
ка. – 2016. – Т. 11, № 1. – С. 64–80. DOI: 10.17537/2016.11.64
5.Методические подходы к расчету вероятности негативных ответов для оценки индивидуальных рисков здоровью человека / Н.В. Зайцева, П.З. Шур, Д.А. Кирьянов, В.М. Чигвин-
цев, О.В. Долгих, К.П. Лужецкий // Профилактическая и клини-
ческая медицина. – 2015. – № 3 (56). – С. 5–11.
6.Нигматулин Р.И. Основы механики гетерогенных сред. –
М., 1978. – 336 с.
7.Фрик П.Г. Турбулентность: подходы и модели. – 2-е изд., испр. и доп. / НИЦ «Регулярная и хаотическая динамика». – М.;
Ижевск, 2010. – 332 с.
8.Цинкер М.Ю. Трехмерное моделирование дыхательной системы человека для задач оценки рисков здоровью при ингаляционной экспозиции химических веществ // Гигиена и санита-
рия. – 2016. – Т. 95, № 1. – С. 90–93.
9.Баренблатт Г.И., Ентов В.М., Рыжик В.М. Теория нестационарнойфильтрациижидкостиигаза. – М.: Недра, 1972. – 288 с.
10.ЛурьеА.И. Теорияупругости. – М.: Наука, 1970. – 940 c.
ОРИЕНТАЦИОННЫЕ ЭФФЕКТЫ В СЛОЕ ФЕРРОНЕМАТИКА ПРИ СУПЕРТВИСТОВЫХ ИСКАЖЕНИЯХ ПОЛЯ ДИРЕКТОРА
М.А. Уткин, Д.В. Макаров
Пермский государственный национальный исследовательский университет,
Пермь, Россия, utkinmaksim@gmail.com, dmakarov@psu.ru
В рамках континуальной теории изучена индуцированная магнитным полем супертвистовая ориентационная структура ферронематического жидкого кристалла. В предельном случае абсолютно жесткого планарного сцепления между директором и намагниченностью в предположении однородного распределения магнитной примеси получены угловые зависимости, определяющие поле директора в ферронематике при различных значениях управляющих параметров системы.
Ключевые слова: ферронематик, жидкий кристалл, супертвистовая деформация.
Под термином «ферронематик» (ФН) понимают суспензию анизометричных магнитных частиц, в которых роль несущей среды играет нематический жидкий кристалл (НЖК) [1–2]. В подоб-
ных мягких средах за счет сцепления молекул нематика на поверхности магнитных частиц имеется возможность создать сильную ориентационную связь между феррочастицами и ЖК-матрицей. Вследствие этого начальная магнитная восприимчивость суспензии повышается по сравнению с чистым нематиком, и в ряде случаев ФН может быть ориентирован относительно слабым внешним полем [3].
Целью настоящей работы является теоретическое описание индуцированных магнитным полем супертвистовых деформаций ориентационной структуры слоя ферронематика и нематика в рамках континуального подхода, сформулированного в основополагающей работе Брошара и де Жена [2].
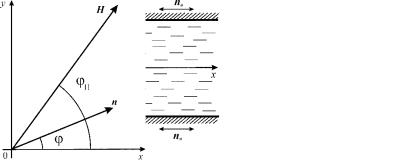
Рассмотрим слой ФН толщиной D , к которому приложим внешнее магнитное поле Н под произвольным углом φH в плоско-
сти слоя(рис. 1).
Рис. 1. Слой ферронематика в магнитном поле Н
Будем считать, что на границах слоя созданы условия жесткого планарного сцепления директора n (направление преимущественной ориентации молекул жидкого кристалла и магнитных частиц) с ограничивающими пластинами. Таким образом, вектор напряженности магнитного поля Н и директор n примут следующий вид:
F ferro
H = H cos φ |
H |
,sin φ |
H |
,0 |
, n = cosφ(z),sin φ(z),0 . |
(1) |
|
|
|
|
|
|
Равновесная ориентационная структура слоя ФН определяется из условия минимума полной свободной энергии [2, 3]:
|
F = FVdV , |
FV = F d + F dia + F ferro + F entr , |
|
(2) |
F d = |
1 |
K11(div n)2 |
+ K 22(n rot n)2 + K 33(n × rot n)2 |
, |
|
2 |
|
|
|
|
|
|
F dia = − |
1 |
χa(n H )2 , |
F ferro = −M s f n H , F entr |
= |
k BT |
f ln f . |
2 |
|
|
|
|
|
v |
|
|
Здесь |
|
F d – потенциал Озеена–Франка; |
K ii – |
константы |
Франка; F dia – диамагнитный вклад, где χa > 0 |
– анизотропия |
диамагнитной восприимчивости нематика, в этом случае директор n стремится ориентироваться вдоль приложенного магнитного поля Н; – дипольный вклад, где M s – намагниченность
насыщения материала феррочастиц, f – локальная объемная доля магнитных частиц в суспензии; F entr – энтропийный вклад, k B
– постоянная Больцмана, T – температура, v – объем феррочастицы. Минимизация функционала свободной энергии ФН (2) приводит к системе дифференциальных уравнений равновесия ФН. В результате интегрирования этих уравнений в бессегрегационном пределе и с учетом симметричности граничных условий получаем:
φ(ζ) |
dφ |
|
= 1 |
φ0 |
dφ |
= 1 |
|
|
|
|
|
− ζ, |
, |
(3) |
|
|
A(φ) |
A(φ) |
0 |
|
|
2 |
0 |
2 |
|
|
A(φ) = |
h2 |
|
(φ0 |
|
|
|
|
+ |
2 |
cos2 |
− φH ) − cos2(φ0 − φH ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
+2bh cos(φ0 − φH ) − cos(φ− φH ) |
|
где φ0 = φ(0) – угол ориентации директора в центре слоя. Здесь ζ – безразмерная координата, h – безразмерная напряженность магнитного поля, параметр b характеризует механизм влияния магнитного поля на ФН (для расчета выбрано значение b = 5 , что соответствует дипольному механизму).
Как видно из рис. 2, в отсутствие внешнего поля угол отклонения директора равен нулю, что соответствует исходной невозмущенной структуре поля директора. При увеличении h угол поворота директора φ0 в центре слоя возрастает и ассим-
птотически приближается к значению угла φH . С ростом φH
на зависимости сначала появляется точка перегиба, а затем и узкая гистерезисная область. В отличие от ФН чистый НЖК (рис. 3) имеет на зависимости точку перегиба и при малых φH ,
а при значении угла ориентации поля φH = π / 2 имеет место
пороговое поле перехода Фредерикса. При фиксированном значении величины h (рис. 4), с ростом угла φH сначала на-
блюдается монотонное увеличение φ0 . Чем больше h , тем
выше на рисунке располагается соответствующая кривая. При последующем увеличении φH , зафиксировав h , наблюдается
уменьшение искажений ориентационной структуры. При больших углах поворота поля на угловой зависимости директора появляются области неоднозначности, которые свидетельствуют о существовании ориентационных переходов 1-го рода в этой области управляющих параметров. При одном и том же значении поля h кривая для ФН располагается выше кривой для НЖК, что соответствует более сильным деформациям поля директора.
Из рис. 5 видно, что при фиксированном значении h с увеличением только лишь φH растёт и отклонение директора от исходной ориентациивовсемслоеФН смаксимумомвцентре слоя.