Физические теории пластичности

скольжение краевых дислокаций осуществляется в плоскостях системы {111} по направлениям <110> [42], γ0 , n – константы материала: харак-

терная скорость сдвигов при равенстве касательных напряжений на СС критическим и константа скоростной чувствительности материала [68],

τ( k ) – действующее в k-й системе скольжения касательное напряжение,

τ(k ) = b(k )n(k ) : σ, H ( ) – функция Хэвисайда, K – число систем сколь-

жения для рассматриваемого типа решетки. Отметим, что число систем скольжения в данном случае равно удвоенному числу кристаллографических систем (в каждой плоскости противоположным направлениям вектора Бюргерса соответствуют разные системы скольжения), т.е., например, для ГЦК-кристалла рассматривается 24 системы скольжения, о – тензор текущей ориентации кристаллографической системы координат кристаллита относительно фиксированной лабораторной системы координат. Скорости сдвигов, накопленные сдвиги, критические напряжения систем скольжения, ориентационный тензор КСК кристаллита являются неявными внутренними переменными мезоуровня.

В качестве определяющего соотношения (уравнения состояния) на мезоуровне выступает закон Гука в скоростной форме (8.30)1, при этом учитывается геометрическая нелинейность: квазитвердое движение [31] связывается с поворотом решетки (кристаллографической системы координат); в коротационной производной тензора напряжений Коши σr фигурирует тензор спина ω, характеризующий скорость вращения кристаллической решетки. Таким образом, напряжения характеризуют именно упругие связи в зерне, связанные с изменением расстояний между соседними атомами. Различные модели поворота решетки подробно рассмотрены в п. 3.4 (см. также [57]).

Уравнение (8.30)2 – кинематическое соотношение, согласно которому неупругое деформирование кристаллита осуществляется за счет сдвигов по системам скольжения.

Для определения скорости неупругого деформирования din в моделях поликристаллических металлов может быть использована [52, 53] либо упругопластическая модель на базе модели Линя [21, 38, 42], либо применяемая в настоящей работе упруговязкопластическая модель (8.30)3, в которых din (как и ω) связывается со скрытыми внутренними переменными мезоуровня, характеризующими дислокационное сколь-

жение – скоростями сдвигов γ(k ) по системам скольжения, k = 1,..., K

201

(K – число систем скольжения для рассматриваемого типа решетки), критическими напряжениями τ(ck ) , тензором о текущей ориентации кри-

сталлографической системы координат зерна относительно фиксированной лабораторной системы координат. Уравнение (8.30)4, описывает эволюцию критических напряжений сдвига по системам скольжения.

Для передачи воздействия, производимого на макроуровне, на низшие масштабные уровни в модели применяется гипотеза Фойгта, согласно которой тензоры деформации скорости для каждого кристаллита совпадают с тензором деформации скорости макроуровня d = D .

В конститутивной модели мезоуровня соотношения (8.30)1 – уравнение состояния, (8.30)3–(8.30)4 – эволюционные уравнения, в качестве замыкающих выступают уравнения (8.30)2, (8.30)5. Классификация внутренних переменных макро- и мезоуровня сведена в табл. 8.1.

8.4. МОДЕЛЬ ПОВОРОТОВ КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ, УЧИТЫВАЮЩАЯ ВЗАИМОДЕЙСТВИЕ ЭЛЕМЕНТОВ МЕЗОУРОВНЯ

Как уже отмечалось выше (см. п. 3.4), наиболее распространенными среди исследователей моделями повоторов кристаллической решетки зерен (далее используется термин «ротации») являются две: модель «полностью стесненного» поворота по Тейлору (3.18) и модель так называемого «материального поворота» (3.22). В качестве серьезного недостатка этих моделей следует отметить отсутствие в них учета микровзаимодействий соседних зерен в поликристалле; по существу, взаимодействие кристаллитов осуществляется на макроуровне за счет используемой гипо-

202

тезы связи уровней (Фойгта, Рейсса и др.). При рассмотрении поликристаллических материалов, для которых можно пренебречь взаимодействием дислокаций в соседних зернах, например, при наличии «толстых» границ аморфного строения в полимерных полукристаллических материалах, применение данных моделей достаточно обоснованно. Однако для металлов экспериментально подтверждено (например, в работах В.Е. Панина [54], В.В. Рыбина [34]), что существенную роль в поворотах решеткииграетнесовместностьскольжениядислокацийвсоседнихзернах.

Вообще говоря, в литературе можно найти достаточно много работ по физическим теориям (в иностранной литературе – crystal plasticity),

вкоторых так или иначе вводятся вращательные степени свободы для кристаллической решетки и строятся кинетические уравнения для поворотов. К принципиальным сложностям таких моделей следует отнести как физическую непрозрачность описания поворотов и причин, приводящих к ним, так и неучет влияния на разворот данного зерна несовместности движения дислокаций в рассматриваемом и в соседних зернах. К одной из немногих работ по физическим теориям пластичности, в которых рассматривается вопрос описания разворотов в поликристалле при помощи явного введения моментных напряжений, относится работа [111], кратко изложенная в п. 3.3. Анализируя рассмотренную работу, остановимся на тех моментах, которые не позволяют использовать ее

вданном исследовании:

♦в работе не приводится физическое обоснование соотношения (3.16) для моментных напряжений, неявно предполагается независимость моментных напряжений от несовместности пластических деформаций в соседних зернах, не указывается физический объем, к которому приложены моментные напряжения;

♦рассматривается поворот, связанный с мгновенной скоростью вращения материальных отрезков, в данный момент образующих ортогональную тройку, совпадающую с главными осями меры скорости деформации, пренебрегается упругими искажениями решетки;

♦не учитывается пороговость необратимых разворотов, что приводит к появлению поворотов элементов уже при малых деформациях.

Введем дополнительные термины, необходимые для описания эволюционирующей структуры поликристалла, которые будут использоваться в дальнейшем. Под «элементом ротации» (ЭР) будем понимать любую структурную составляющую микроструктуры (зерно, субзерно, фрагмент) или их совокупность, способную к разворотам как целое, с со-

203

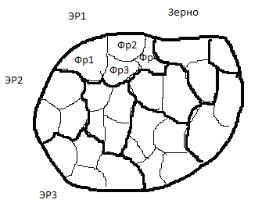
хранением (с приемлемой точностью) правильного кристаллического строения решетки составляющих, их взаиморасположения и взаимоориентации (рис. 8.3). Здесь следует отметить, что, вообще говоря, размер ЭР, претерпевающего разворот, заранее не известен. Более того, эксперименты показывают, что с увеличением интенсивности деформаций характерные размеры разворачивающихся элементов структуры изменяются [10, 28, 34]. Для определения ЭР в каждый момент деформирования в работе вводится еще один тип структурных элементов, которые в каждый момент деформирования могут образовывать ЭР (по определенному алгоритму, о котором будет изложено ниже). Под «зерном» будем понимать наименьший объем материала, который (по крайней мере, на начальный момент деформирования) с приемлемой точностью можно считать монокристаллическим телом. Под «фрагментами зерна» будем понимать микрообласти материала, разориентированные относительно друг друга на углы порядка нескольких минут или градусов [34]. Надо отметить, что введение понятия «элемент ротации» не подменяет понятий «зерно» и «фрагмент зерна», так как, вообще говоря, в произвольный момент деформирования в качестве ЭР могут выступать и фрагмент, и группа фрагментов, и зерно (и даже совокупность зерен).

Рис. 8.3. К выделению структурных элементов

В работах [40, 41] одной из причин разворотов решетки зерен (кроме так называемого «материального» поворота) считается несовместность сдвигов по системам скольжения в соседних зернах (моделирующих, в свою очередь, движение дислокаций). Тогда скорость изменения вектора поверхностного момента, действующего на часть границы анализируемого зерна (фрагмента зерна) в результате сопротивления

204

где ( )r – соответствующая коротационная производная (вопрос о ее вы-

боре обсуждается ниже), (mr )m – составляющая скорости вектора момен-

та, обусловленная несовместностью сдвига в данном фрагменте со сдвигами в соседнем m-м фрагменте, М – число соседних фрагментов.

Эволюция вектора-момента mm определяется следующим соотношением:

где λ – экспериментально определяемый (в Па м) параметр, N – внешняя для анализируемого фрагмента единичная нормаль к границе

1)В соотношении (8.34) явно учитываются несовместность сдвигов и ориентация границы.

2)Рассмотрим случай отсутствия сдвигов в соседнем зерне (что согласно модели эквивалентно нахождению зерна в жесткой оболочке).

205

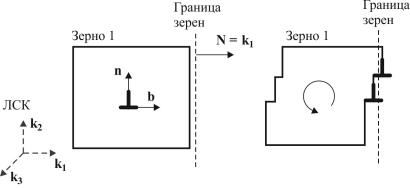
Для простоты будем рассматривать случай, когда активна одна СС (индекс отбросим). Тогда m = µ γ N × nb N .

Рис. 8.4. Схема для пояснения N = k1 , b = k1 , n = k2

Например, для случая, изображенного на рис. 8.4,

m = k × γk k k = µ γk . При γ > 0 в верхней части границы вследст-

1 2 1 1 3

вие прохождения дислокаций по СС возникает избыток атомов, в нижней части – недостаток, поэтому скорость момента направлена против часовой стрелки.

3)Векторную часть (8.34), порождаемую операцией векторного умножения « N », можно трактовать как вектор линии дислокации ориентационного несоответствия [34], залегающей в границе. Логично, что скорость момента, действующего на зерно, направлена вдоль этойлинии.

4)Скалярные произведения « N » характеризуют, каким образом сдвиг по СС ориентирован по отношению к границе. Например, в случае, когда направление сдвига по СС перпендикулярно нормали к границе, соответствующая составляющая будет нулевой, что согласуется

сфизическим анализом.

Соотношение (8.34) перекликается с приведенным в работе [34]:

206

разность пластических составляющих деформаций в зернах n и n’. Однако имеется ряд отличий между предлагаемым соотношением (8.34) и содержащимсявцитируемойработе(8.35):

–в соотношении (8.35) используется симметричный тензор деформации, что представляется не совсем корректным с точки зрения описания движения дислокаций (вторая часть ориентационного тензора не соответствует реальной СС),

–соотношение (8.35) не предполагает пороговости: изменение вектора начинается, как только начинается пластическое деформирование в соседних зернах, что также не соответствует физике процесса. Для обеспечения пороговости «решеточного» поворота вводится силовой фактор – моментные напряжения, чтобы затем явно задать критерий реализуемости решеточного поворота в замыкающем уравнении для связи спина решетки с моментными напряжениями.

При этом стоит отметить, что в работе [34] делается попытка обоснования соотношения (8.35) на основе физических и математических посылок: вводятся дислокации ориентационного несоответствия,

тензор их плотности ∆ B(nn' ) , выводится уравнение для изменения B(nn' )

в зависимости от деформации, затем автор приходит к соотношению (8.35). Соответствующие выкладки были проведены как для соотношения (8.35), так и для соотношения (8.34). Несмотря на ряд возникших при этом вопросов, такой путь – построение феноменологических моделей путем анализа физики процесса на меньших масштабных уровнях – представляется продуктивным.

Определим вид коротационной производной, которую необходимо применить в соотношениях (8.31)–(8.32) для соблюдения принципа материальной индифферентности. Пусть на элемент ротации, а также на все фрагменты, которые его окружают, накладывается поворот как жесткого целого. В этом случае очевидно, что и вектор (тензор) моментных напряжений испытает такой же поворот. Также отметим, что при расчетах для отдельного фрагмента все величины (деформации скорости, напряжения, тензор упругих свойств, сдвиги по системам скольжения, моменты) определяются с точки зрения наблюдателя, находящегося в кристаллографической системе координат; к этой же системе координат жестко «привязан» материал фрагмента. Поскольку вращение КСК осуществляется по отношению к лабора-

207

торной системе координат (ЛСК) как жесткого целого (вместе с материалом), то для удовлетворения принципа материальной индифферентности необходимо выбрать тип коротационной производной, «привязанной» к угловой скорости вращения кристаллической решетки, следовательно,

где Ω – тензор спина кристаллической решетки фрагмента, определяемый в каждый момент деформирования как тензор, ассоциированный с вектором угловой скорости вращения решетки ω, Ω = − Є ω, Є – тензор Леви–Чивита.

Тогда окончательно для поверхностных моментов имеем:

m=1

где по индексу m нумеруются составляющие момента на отдельных фасетках данного элемента ротации (кристаллита).

Скорость поворота (спин) решетки ω представляется суммой двух составляющих. Первая составляющая ω1 описывает поворот решетки

вместе с материалом зерна при наложенном кинематическом воздействии, назовем эту составляющую «материальным поворотом». Связывая материальный поворот с ортогональным тензором, сопровождающим упругую деформацию, данную составляющую предлагается определять как ω1 = wre . Вторая составляющая скорости поворота ω2 («решеточ-

ный поворот») характеризует ротацию собственно решетки кристаллита, обусловленную взаимодействием с окружением.

Составляющая спина решетки ω2 определяется соотношением:

208

Разностный аналог метода Адамса–Моултона второго порядка для

Поскольку для рассматриваемой системы уравнений аналитическое решение системы типа (8.40), как правило, не существует, то предлагается находить с помощью итерационного процесса вида:

станта в условии Липшица для правой части исходного дифференциального уравнения.

В качестве начального приближения выбирается yk(0)+1 = yk . Тогда на первой итерации получаем решение

соответствующее использованию явной схемы Эйлера, имеющей первый порядок аппроксимации. Далее,

что для рассматриваемого одномерного случая соответствует схеме Рунге–Кутта второго порядка

210