
Физические теории пластичности
..pdf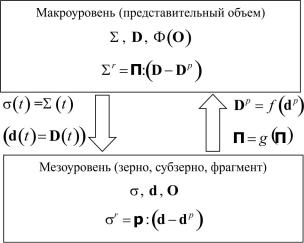
Рис. 8.2. Схема двухуровневой модели
Как любая методика, двухуровневый подход имеет свои достоинства и недостатки. К достоинствам подхода можно отнести:
♦возможность моделирования мезоструктуры поликристалла (распределение ориентаций КСК зерен, их размер и форму);
♦моделирование макросвойств, существенно зависящих от мезоструктуры, в частности, анизотропию упругих, пластических и прочностных свойств;
♦относительно простой вид определяющих соотношений макроуровня (например, анизотропный закон Гука в релаксационной скоростной форме);
♦возможность распараллеливания вычислений;
♦применимость к решению существенно нелинейных задач. Среди недостатков данного подхода можно отметить:
♦невозможность получения аналитического решения задачи;
♦большое количество неявных внутренних переменных для описания мезоуровня;
♦большие запросы по ресурсам памяти и времени ЭВМ;
♦высокую трудоемкость разработки программ для ЭВМ.
Многие из отмеченных недостатков носят непринципиальный характер, особенно в свете развития вычислительных технологий. Например, затраты машинного времени можно значительно снизить, используя распараллеливание алгоритма. При этом процедура распараллеливания может быть осуществлена как по отдельным элементам мезоуровня (зернам, фрагментам и т.д.), так и по ПО макроуровня. Для распаралле-
191
ливания цикла по совокупностям ПКА удобно использовать технологию MPI. Более трудоемким является распараллеливание внутренних по отношению к макроуровню циклов и методов решения СЛАУ макрозадачи. Возможно, что в этом случае больший выигрыш можно получить от использования технологии OpenMP, ориентированной на многоядерность микропроцессоров.
8.2. СОГЛАСОВАНИЕ ОПРЕДЕЛЯЮЩИХ СООТНОШЕНИЙ МАСШТАБНЫХ УРОВНЕЙ И КОНКРЕТИЗАЦИЯ НЕЗАВИСЯЩЕЙ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЕТА ПРОИЗВОДНОЙ
Одним из часто возникающих вопросов при построении двухуровневых (и в общем случае многоуровневых) моделей, использующих гипотезу Фойгта, является следующий: почему возникает излишняя информация о напряжениях на макроуровне? Действительно, с одной стороны, на макроуровне напряжения определяются из закона Гука в скоростной релаксационной форме, в который входят осредненные скорости неупругих деформаций, определяемые в модели мезоуровня. С другой стороны, напряжения макроуровня можно определить осреднением напряжений мезоуровня. При этом нет оснований утверждать, что вычисленные этими двумя способами напряженные состояния окажутся идентичными или хотя бы близкими.
Однако следует помнить, что на макроуровне остается нерешенной проблема выбора квазитвердого движения и соответствующей коротационной производной в законе Гука. Ниже приведен алгоритм выбора коротационной производной и выражения для скорости неупругой деформации, обеспечивающие согласование определяющих соотношений различных масштабных уровней. Отметим, что с методической точки зрения достаточно провести согласование двух соседних масштабных уровней, для остальных все выкладки аналогичны.
Рассмотрим два соседних масштабных уровня некоторой многоуровневой модели, величины на верхнем масштабном уровне будем обозначать большими буквами, на нижнем масштабном уровне – малыми. Для определенности примем, что определяющее соотношение верхнего уровня записывается в форме
Σ+ AT Σ+ Σ A = Π: (D − Din ) , |
(8.2) |
192
нижнего уровня (для каждого элемента из выборки, соответствующей представительному объему верхнего уровня) – в виде
σ+ aT σ+ σ a = π: (d − din ) . |
(8.3) |
В соотношениях (8.2) и (8.3) не конкретизируется вид тензоров А, а, характеризующих движение подвижных систем координат на верхнем и нижнем (для каждого элемента) масштабном уровне, относительно которой определяется квазитвердное движение, в частности, не накладывается условие антисимметричности; необходимым условием является только индифферентность ассоциированных с этими тензорами производных от индифферентных тензоров – для обеспечения выполнения независимости определяющих уравнений (8.2), (8.3) от выбора системы отсчета.
Представим величины, входящие в описание напряженно-дефор- мированного состояния элемента нижнего уровня, в виде суммы средних по представительному объему верхнего уровня величин и отклонений от этих средних:
π=< π> +π′, σ =< σ > +σ′, d =< d > +d′,
(8.4)
din =< din > +din′, a =< a > +a′,
где < > – оператор осреднения, обладающий свойством:
< π′ >= 0, < σ′ >= 0, < d′ >= 0, < din′ >= 0, < a′ >= 0 . |
(8.5) |
Вид используемого оператора осреднения не обсуждается, например, может использоваться осреднение по объему или осреднение в пространстве ориентаций решеток кристаллитов, важно лишь выполнение свойства (8.5) для используемого оператора осреднения.
Подставляя представление (8.4) в определяющее уравнение нижнего уровня (8.3), получаем соотношение:
< σ > +σ′ + (< aT > +aT′) (< σ > +σ′) + (< σ > +σ′) (< a > +a′) =
(8.6)
= (< π> +π′) : (< d > +d′− < din > −din′).
193
Осредняя (8.6), имеем
< σ > + < aT > < σ > + < aT′ σ′ > + < σ > < a > + < σ′ a′ >=
(8.7)
= < π> : (< d > − < din >) + < π′ : (d′ − din′) > .
Примем, что согласование напряженно-деформированного состояния на различных уровнях заключается в равенствах:
Π=< π> , Σ =< σ > , D =< d > . |
(8.8) |
Соотношение (8.8) устанавливает, что эффективные свойства и характеристики напряженно-деформированного на верхнем масштабном уровне должны быть в точности равны осредненным характеристикам нижнего масштабного уровня.
При условии (8.8) соотношение (8.7) представляется в виде
Σ + < aT > Σ+ Σ < a > + < aT′ σ′ > + < σ′ a′ >=
(8.9)
= Π: (D − < din >) + < π′ : (d′ − din′) > .
Сравнивая (8.9) с формой определяющего уравнения на верхнем уровне (8.2), можно получить уравнения, связывающие параметры верхнего уровня A, Din с параметрами нижнего уровня, обеспечивающие выполнение условий согласования (8.8). При этом возникают, по крайней мере, два возможных варианта определения A, Din .
В первом случае напрямую сопоставляются левые и правые части соотношений (8.9) и (8.2), откуда следует связи параметров уровней:
A =< a > +Σ−1 < σ′ a′ >, AT =< aT > + < aT′ σ′ > Σ−1 , |
(8.10) |
|||||||||
D |
in |
=< d |
in |
−1 |
′ |
′ |
− d |
in′ |
) > . |
(8.11) |
|
|
> − Π |
: < π |
: (d |
|
|||||
Тензор A , определенный согласно (8.10), в общем случае не является антисимметричным, −A ≠ AT . В этом случае левую часть определяющего соотношения верхнего уровня (8.2) следует трактовать как конвективную производную тензора напряжений Коши. Для рассматриваемых многоуровневых моделей можно показать, что полученная кон-
194
вективная производная является индифферентной по отношению к наложенному жесткому движению.
Необходимым и достаточным условием антисимметричности А (при условии антисимметричности тензора а и симметрии тензоров напряжений макро- и мезоуровня) является следующее:
Σ−1 < σ′ a′ >=< aT′ σ′ > Σ−1 . |
(8.12) |
При выполнении условия (8.12) на макроуровне конвективная производная выродится в коротационную производную. Для получения A =< a > необходимым и достаточным условием будет являться:
< aT′ σ′ > + < σ′ a′ >= 0 .
Отметим, что трактовка движения подвижной системы координат, определяемой (8.10), достаточно сложна: во-первых, в данной системе координат меняются длины базисных векторов и углы между ними, вовторых, характеризующий движение тензор А явно зависит от Σ.
Всоотношении (8.11) к собственно неупругим деформациям добавляется член, характеризующий коррелированные (с флуктуациями компонент тензора упругих характеристик) напряжения.
Вслучае использования в статистических моделях для передачи на
нижний уровень условий нагружения гипотезы Фойгта ( d = D , d′ = 0 ) связи (8.10)–(8.11) принимают вид:
A =< a > +Σ−1 < σ′ a′ >, AT =< aT > + < aT′ σ′ > Σ−1 , |
(8.13) |
Din =< din > + Π−1: < π′ : din′ > . |
(8.14) |
При использовании гипотезы Рейсса σ = Σ, σ' = 0 соотношения
(8.10)–(8.11) принимают вид:
|
|
|
|
A =< a > , |
|
|
|
|
(8.15) |
|
D |
in |
=< d |
in |
−1 |
′ |
′ |
− d |
in′ |
) > . |
(8.16) |
|
|
> − Π |
: < π : (d |
|
|
|||||
При антисимметричных тензорах a , т.е. при коротационных производных на нижнем масштабном уровне в законе (8.3), помимо вышеизложенного подхода для определения зависимостей A, Din от парамет-
195
ров нижнего уровня предлагается альтернативный вариант. При антисимметричном a соотношение (8.9) принимает вид:
Σ− < a > Σ+ Σ < a > − < a′ σ′ > + < σ′ a′ >=
(8.17)
= Π: (D − < din >) + < π′ : (d′ − din′) > .
Анализируя левую часть соотношения (8.17), можно структуре
Σ− < a > Σ+ Σ < a > дать трактовку коротационной производной Σ (спин подвижной системы координат верхнего уровня определяется как < a > ). Последний симметричный член в правой части
( − < a′ σ′ > + < σ′ a′ > ) можно трактовать как дополнительный вклад, характеризующий скорость изменения напряжений за счет коррелированных разворотов элементов нижележащего уровня со своими отклонениями напряжений от среднего уровня. Перенося этот член
вправую часть, имеем:
Σ− < a > Σ+ Σ < a >=
(8.18)
= Π: (D − < din >) + < π′ : (d′ − din′) > +(< a′ σ′ > − < σ′ a′ >).
Сопоставляя соотношения (8.18) и (8.2), можно определить связи параметров уровней следующим образом:
A =< a >, |
(8.19) |
Din =< din > − Π−1: < π′ : (d′ − din′) > − Π−1: ( < a′ σ′ > − < σ′ a′ > ) . |
(8.20) |
При таком подходе на верхнем уровне получается коротационная производная. Жесткую подвижную систему координат можно трактовать как некоторый трехгранник, вращающийся с угловой скоростью, определяемой осредненным спином A =< a > .
В случае использования в статистических моделях для передачи на нижний уровень условий нагружения гипотезы Фойгта ( d = D , d′ = 0 ) связи (8.19)–(8.20) принимают вид:
A =< a > , |
(8.21) |
Din =< din > + Π−1: < π′ : din′ > − Π−1: ( < a′ σ′ > − < σ′ a′ > ) . (8.22)
196
При использовании гипотезы Рейсса |
σ = Σ, σ' = 0 |
соотношения |
||||||||
(8.190)–(8.20) принимают вид: |
|
|
|
|
|
|
||||
|
|
|
|
A =< a > , |
|
|
|
(8.23) |
||
D |
in |
=< d |
in |
−1 |
′ |
′ |
− d |
in′ |
) > . |
(8.24) |
|
|
> − Π |
: < π |
: (d |
|
|||||
Отметим, что несмотря на различные связи параметров (и различие в используемых физических трактовках), соотношения (8.13)–(8.14) и соотношения (8.19)–(8.20) приводят к одному и тому же определяю-
щему уравнению для напряжения Σ на верхнем уровне и выполнению условий согласования (8.8).
Таким образом, условие согласования определяющих уравнений различных масштабных уровней приводит к конкретизации вида определяющего соотношения на макроуровне (и, в частности, – вида независящей от выбора системы отсчета производной). По существу, соотношения низшего уровня «транспортируются» на верхний, разрешая вопрос корректной их формулировки для геометрически и физически нелинейной задачи. Действительно, параметры определяющего соотношения верхнего уровня определены с целью выполнения (8.8), и при реализации модели отсутствует необходимость интегрирования определяющего уравнения верхнего уровня – достаточно напрямую воспользоваться связью Π=< π> , Σ =< σ > , D =< d > . В то же время следует отметить, что определяющие соотношения верхнего масштабного уровня необходимы для постановки и решения соответствующей краевой задачи исследования деформирования макроскопического тела (детали, конструкции).
При подобном подходе (как и при применении многоуровневого подхода в целом), конечно, возникает вопрос о степени корректности модели низшего уровня, восходящий к известной проблеме замыкания эволюционных и определяющих уравнений (наиболее известным примером может служить проблема замыкания в теории турбулентности). Суть проблемы состоит в том, что при формулировке физических уравнений для представительного объема некоторого уровня возникает необходимость введения параметров меньшего масштабного уровня и эволюционных уравнений для них и так далее – вниз по «лестнице масштабов». Можно отметить два наиболее употребительных подхода к ее решению. В первом – феноменологическом – параметры, характе-
197
ризующие структуру на более низких масштабных уровнях, определяются функциональными уравнениями через параметры рассматриваемого уровня (например, как в модели турбулентности Рейнольдса) с последующей экспериментальной проверкой этих уравнений. Второй подход основан на построении иерархической совокупности моделей нескольких масштабных уровней – многоуровневое моделирование. Следует отметить, что в этом случае полностью избежать феноменологических соотношений, конечно, не удается, однако они записываются для самого низкого масштабного уровня в принятой иерархической совокупности, для которого возможны конкретизация физических механизмов деформирования и детальное их описание с использованием известных положений физики твердого тела (это представляется существенно более простой задачей по сравнению с задачей установления макрофеноменологических соотношений, одновременно учитывающих состояние многомасштабной внутренней структуры и описывающих многообразие всех механизмов неупругого деформирования).
Отметим, что предложенную методику легко применить и при другой форме определяющих соотношений на мезо- и макроуровнях для широкого класса конститутивных моделей с использованием внутренних переменных (когда определяющие соотношения являются дифференциальными, например, для соотношений максвелловского типа).
Для двухуровневой модели поликристаллических металлов используются следующие связи (конкретизация замыкающих соотношений макроуровня):
Ω =< ω > +Σ−1 < σ′ ω′ > , |
(8.25) |
Din =< din > + Π−1: < π′ : din′ > |
(8.26) |
либо (согласно второму подходу) |
|
Ω =< ω > , |
(8.27) |
Din =< din > + Π−1: < π′ : din′ > − Π−1: ( < ω′ σ′ > − < σ′ ω′ > ). |
(8.28) |
198
8.3. КЛАССИФИКАЦИЯ ВНУТРЕННИХ ПЕРЕМЕННЫХ И УРАВНЕНИЙ КОНСТИТУТИВНОЙ МОДЕЛИ НА ПРИМЕРЕ ДВУХУРОВНЕВОЙ УПРУГОВЯЗКОПЛАСТИЧЕСКОЙ МОДЕЛИ
На макроуровне рассматривается представительный объем поликристаллического металла, состоящий из совокупности кристаллитов – элементов мезоуровня.
Конститутивная модель материала на макроуровне принимается в виде:
|
Σ |
|
≡ |
Σ+ Ω |
|
Σ+ Σ Ω= Π: D |
|
= Π: (D − D |
|
), |
||
|
|
r |
|
|
|
T |
|
e |
|
in |
|
|
Ω = Ω(ω(i ) , π(i ) ), i = 1,..., N , |
|
|
|
(8.29) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Π= Π(π(i ) , |
o(i ) ), i = 1,..., N , |
|
|
|
|
|||||||
|
|
in |
|
= D |
in |
|
in |
, π(i ) ), i = 1,..., N , |
|
|
|
|
D |
|
|
|
(d(i ) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
где Σ – тензор напряжений Коши, Π– тензор модулей упругости, D, De , Din – тензор деформации скорости, его упругая и неупругая состав-
ляющая соответственно, индекс r означает независящую от выбора системы отсчета производную, Ω – тензор, описывающий движение подвижной системы координат, относительно которой определяется собственно деформационное движение [31] на макроуровне. Стоит акцентировать внимание на том, что вопрос однозначного введения независящей от выбора системы отсчета производной, т.е. корректного разложения движения на квазитвердое и собственно деформационное – один из наиболее трудных в нелинейной механике деформируемого твердого тела [31] и, по мнению авторов, не решен до сих пор. Для определения Ω предлагается использовать условие согласования определяющих соотношений на различных масштабных уровнях.
Таким образом, неупругая составляющая деформации скорости Din , эффективные анизотропные упругие свойства Π и описывающий движение подвижной системы координат тензор Ω являются явными внутренними переменными модели макроуровня, в каждый момент зависят от структуры на низших масштабных уровнях (а через нее – от истории нагружения) и определяются с помощью модели мезоуровня (N – число элементов мезоуровня, необходимых для статистического описания представительного объема макроуровня, далее индекс элемента мезо-
199
уровня опускается). Параметры din(i ) , π(i ) , ω(i ) представляют собой неяв-
ные внутренние переменные макроуровня.
Согласно вышеприведенной общей структуре конститутивной модели (8.29) 1 является уравнением состояния, а (8.29)2–(8.29)4 – замыкающими уравнениями, конкретизация которых является одной из основных целей работы (предлагаемый авторами подход описан в п 8.2); в качестве эволюционных уравнений выступают соотношения модели мезоуровня.
На мезоуровне (уровне кристаллита) в двухуровневых моделях неупругого деформирования поликристаллических металлов используется следующая система соотношений:
σr ≡ σ− ω σ+ σ ω= π: de = π: (d− din ), |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
in |
K |
γ |
(k ) |
|
(k ) |
, |
|
|
|
|
|
|
||||
d |
|
= ∑ |
|
|
m(S) |
|
|
|
|
|
|
||||||
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
(k ) |
|
1/n |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
(k ) |
|
|
|
|
|
|
|
|
|
(k ) |
|
(k ) |
|
|
|
|
γ |
|
= γ0 |
|
|
|
|
|
|
|
|
H (τ |
|
− τc |
|
), k = 1,..., K , |
|
(8.30) |
|
|
τc(k ) |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
= f (γ(j ) , γ(j ) ), k, |
j = 1,..., K , |
|
|
||||||||||||
τc(k ) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
= ω, |
соотношения для определения спина решетки ω, o o |
|
||||||||||||||||
d = D, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где σ – тензор напряжений Коши, π – тензор четвертого ранга упругих свойств кристаллита, d, de , din , ω – тензор деформации скорости, его упругая и неупругая составляющие на мезоуровне и тензор спина КСК, параметры π, din , ωявляются явными внутренними переменными мезоуровня, γk , τCk – накопленный сдвиг и критическое напряжение сдвига по k-й системе скольжения, m((S)k ) – симметричная часть ориентационного тензора k-й системы скольжения, m((S)k ) = 1/ 2(b(k )n(k ) + n(k )b(k ) ) , b(k ) , n(k ) – единичные векторы в направлении вектора Бюргерса и нор-
мали к плоскости скольжения; плоскости залегания и ориентация векторов Бюргерса, вдоль которых осуществляется трансляционное движение (скольжение) краевых дислокаций, известны, ими являются наиболее плотно упакованные плоскости и направления; так, в ГЦК-металлах
200
