Введение в математическое программирование

УДК 519.85(075.8) Т66

Рецензенты:

канд. физ.-мат. наук, доцент кафедры прикладной математики

М.А. Севодин

(Пермский государственный технический университет); зав. кафедрой охраны окружающей среды

д-р физ.-мат. наук, профессор кафедры высшей математики

В.Ф. Панов

(Пермский государственный университет)

Третьякова, Н.Г.

Т66 Введение в математическое программирование: учеб. пособие / Н.Г. Третьякова. – Пермь: Изд-во Перм. гос. техн.

ун-та, 2007. – 103 с.

ISBN 978-5-88151-707-6

Содержит основные теоретические сведения по линейному программированию, его применению к решению оптимизационных экономических задач.

Приведены геометрический способ решения задач линейного программирования, симплекс-метод, метод искусственного базиса, метод потенциалов для решения задач транспортного типа, основные положения и теоремы теории двойственности.

Рассмотренынекоторыевопросынелинейногопрограммирования. Даны подробные решения типовых экономических задач оп-

тимизации.

Предназначено для студентов экономических специальностей дневной и заочной форм обучения, а также для широкого круга читателей, интересующихся применением математических методов в экономике.

УДК 519.85(075.8)

©ГОУ ВПО «Пермский государственный

ISBN 978-5-88151-707-6 технический университет», 2007

2

3

ВВЕДЕНИЕ

Учебное пособие посвящено задачам, в которых моделируются различные процессы, исследуемые в экономике.

Первая глава пособия посвящена предмету математического программирования.

Во второй главе дана классификация математических моделей по критериям оптимальности, структуре ограничений, учету неизвестных факторов, виду неопределенности.

Третья глава – основная. Она посвящена вопросам линейной оптимизации. В этой главе даны основные теоретические сведения по линейному программированию, приведено большое количество примеров, рассмотрены специальные задачи линейного программирования.

Вчетвертой главе рассмотрены вопросы нелинейной оптимизации.

Взаключении приведены варианты заданий для контрольных работ (30 вариантов). Примеры носят учебный характер

ирассчитаны на вычисления «вручную».

ГЛАВА I

Предмет математического программирования

При рассмотрении многих планово-экономических и производственных вопросов часто возникает задача выбора наиболее рационального или, как принято говорить, оптимального решения, когда из всех решений, возможных в данных условиях, требуется найти такое, которое в известном смысле является наилучшим. Задачи такого типа возникают при планировании перевозок, составлении производственных планов предприятия, составлении различных смесей и т.д.

В большинстве таких задач требуется найти экстремум (максимум или минимум) целевой функции при различных ограничениях, накладываемых на переменные.

Особый класс составляют задачи линейного программирования, когда целевая функция линейна, а ограничения задаются линейными уравнениями или неравенствами.

Для решения такого рода задач и разработаны специальные методы, основанные на выборе оптимального варианта в процессе математического исследования. Эти методы объединены под общим названием – математическое программирование.

4

Итак, математическое программирование (МП) – раздел математики, разрабатывающий теорию и численные методы решения задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных.

Решение экономической задачи начинается с составления ее математической модели. Математическая модель отражает проблему в абстрактной форме и позволяет учесть большое число разнообразных характеристик, от которых зависит эта проблема.

Математическая модель задачи МП включает в себя:

1.Совокупность неизвестных величин x1, x2 , ..., xn . Эту совокупность неизвестных величин называют планом задачи или решением и обозначают X = (x1, x2 , ..., xn ) .

2.Систему ограничений (условий), налагаемую на неизвестные величины. Эти условия следуют из ограниченности ресурсов, которыми располагает общество в любой момент времени, из условий производственных и технологических процессов

ит.д. Математически ограничения выражаются в виде уравнений

инеравенств. Множество планов, удовлетворяющих системе ог-

раничений, образует область допустимых решений Ω. В соответствии с условиями задачи на все переменные или на некоторые из них накладываются условия неотрицательности.

3. Целевую функцию Z = Z(X ) . Функция Z называется це-

левой, т.к. представляет формальное описание некоторой цели, которая фигурирует в содержательной задаче оптимизации. Целевая функция позволяет выбрать наилучший вариант среди множества допустимых решений.

Таким образом, в общем виде задача математического программирования ставится следующим образом:

где ϕi и Z – заданные функции; bi – некоторые действительные числа.

5

Требуется среди решений системы (1.1)–(1.2) найти такое решение, при котором целевая функция (1.3) примет экстремальное (максимальное или минимальное) значение.

Система ограничений (1.1) называется системой специальных ограничений, а система (1.2) – системой общих ограничений задачи МП. Общие ограничения (если они есть) одинаковы для любых задач МП, специальные – отражают особенности конкретной задачи МП.

План X , удовлетворяющий системе ограничений задачи

(1.1)–(1.2), называется допустимым (X Ω).

Допустимый план, при котором целевая функция (1.3) принимает экстремальное значение, называется оптимальным. Оп-

тимальный план будем обозначать X , экстремальное значение целевой функции Z = Z(X ) .

ГЛАВА II Классификация математических моделей

В математическом программировании рассматривается широкий круг экономических задач, математические модели которых очень разнообразны.

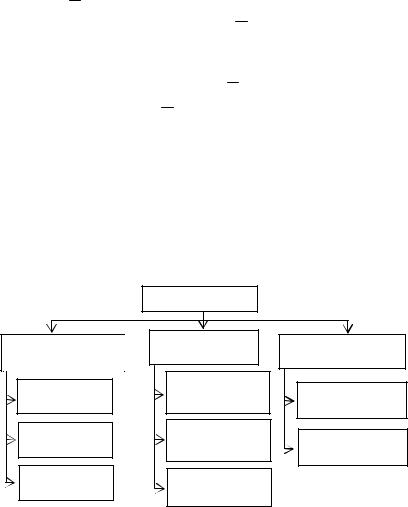
Автором предлагается классификация математических моделей, взятая из работы [7]:

Данное учебное пособие посвящено изучению детерминированных моделей.

Многие экономические задачи могут быть изучены и решены с использованием детерминированных моделей. По виду целевой функции и функций, входящих в ограничения задачи, детерминированные модели делятся на линейные, нелинейные

идинамические.

Влинейных моделях целевая функция и функции, входящие в систему ограничений задачи, являются линейными относительно входящих в задачу неизвестных. Изучением линейных моделей занимается линейное программирование.

Линейное программирование является наиболее разработанным разделом математического программирования, поэтому к линейным моделям стараются свести самые разнообразные экономические задачи либо на этапе постановки, либо в процессе решения.

Методы и модели линейного программирования применяются во всех отраслях народного хозяйства: при разработке производственной программы предприятия, при определении наилучшего ассортимента выпускаемой продукции, в задачах перспективного и текущего планирования и управления, при планировании грузопотоков, определении плана товарооборота

иего распределении и т.д.

Внелинейных моделях либо целевая функция, либо хотя бы одна из функций, входящих в систему ограничений, нелинейна относительно управляющих переменных задачи.

Если параметры целевой функции и (или) системы ограничений изменяются во времени или целевая функция имеет аддитивный или мультипликативный вид, или сам процесс выработки решений имеет многошаговый характер, то такие задачи решаются методами динамического программирования.

Встохастических моделях параметры, входящие в функцию цели и ограничения задачи, являются случайными величинами.

Для моделирования ситуаций, зависящих от факторов, для которых невозможно собрать статистические данные и значения которых не определены, используются модели с элементами неопределенности.

7

ГЛАВА III Линейное программирование

Начало линейному программированию было положено в 1939 г. советским математиком-экономистом Л.В. Канторовичем в работе «Математические методы организации и планирования производства». Термин «программирование» соответствует не очень удачному переводу английского «programmation». Под линейным программированием понимается линейное планирование, т.е. получение оптимального плана – решения в задачах с линейной структурой.

Линейное программирование (ЛП) – раздел МП, предназначенный для отыскания экстремума линейной функции нескольких переменных при линейных ограничениях, налагаемых на эти переменные.

По типу решаемых задач методы ЛП разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи ЛП. Специальные методы разработаны для решения определенного класса экономических задач.

3.1. Примеры построения математических моделей экономических задач

Приведем примеры некоторых типовых экономических задач, оптимальное решение которых может быть найдено с помощью построения и расчета соответствующих линейных математических моделей.

1. Задача об оптимальном использовании ресурсов (задача планирования производства)

Предприятие может производить n видов продукции – Ï 1, Ï 2 , ..., Ï n . Производство каждого вида требует затрат дефицитных материалов, производственных мощностей и трудовых ресурсов. Всего используется m видов ресурсов – S1, S2 , ... , Sm ,

причем i-м ресурсом предприятие располагает в количестве bi единиц.

8

Известна экономическая выгода производства продукции каждого вида: c j − доход предприятия от реализации единицы

j-го продукта; aij −затраты i-го ресурса при производстве еди-

ницы j-го продукта.

Требуется составить такой план производства продукции, который обеспечил бы предприятию максимальную прибыль от реализации продукции.

Составим математическую модель задачи:

Обозначим через xj количество изделий вида Пj, планируемое к производству. Тогда X = (x1, ..., xn ) – план производства.

Подсчитаем общую прибыль предприятия от реализации всей производимой продукции. Обозначим ее через Z

(Z (X ), Z(x1, x2 , ..., xn )).

n

Z = ∑c j x j .

j =1

Это целевая функция, которую нужно максимизировать. Подсчитаем расход i-го ресурса на изготовление всех видов продукции. Он не должен превосходить запаса bi соответствующего ресурса:

ai1x1 + ai2 x2 +... + ain xn ≤bi (i =1, m) .

Получаем систему ограничений нашей задачи. Кроме того, по смыслу задачи необходимо наложить условие неотрицательности на все переменные задачи:

x j ≥ 0 ( j =1, n) .

Таким образом, модель задачи об оптимальном использовании ресурсов примет следующий вид:

найти максимум функции

n

Z = ∑c j x j (3.1.1)

j=1

9

при ограничениях

Так как функция Z(X ) и неравенства, входящие в систему ограничений, линейны относительно переменных x j , а параметры aij , bi , c j являются постоянными величинами в плани-

руемый период, то (3.1.1)–(3.1.3) – задача линейного программирования (ЗЛП).

2. Транспортная задача

Рассмотрим простой вариант транспортной задачи, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям; при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по удовлетворению спроса. Причем потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. Так возникает задача о наиболее рациональном прикреплении, правильном направлении перевозок грузов, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, а затраты на транспортировку минимальны.

Задача формулируется так: имеется m пунктов производства, в каждом из которых сосредоточено ai (i =1, m)единиц однородного продукта. Этот продукт нужно доставить n потребителям, потребность j-го потребителя составляет bj (j =1, n)единиц.

Известны величины cij – затраты на перевозку единицы продукта из i-го пункта производства в j-й пункт потребления.

Требуется составить такой план перевозки продукции от поставщиков к потребителям, при котором суммарные транспортные издержки будут минимальны.

10