Введение в математическое программирование

Решим задачу графически. Построим область допустимых решений. Построим граничные прямые, соответствующие данным ограничениям-неравенствам:

Затем определим полуплоскости, соответствующие каждому неравенству нашей системы. Для этого достаточно взять произвольную точку, не лежащую на граничной прямой, и подставить ее координаты в соответствующее неравенство. Для всех четырех неравенств в качестве пробной точки можно взять, например, начало координат О (0, 0). Получим истинные утвер-

Z=0 (2)

Рис. 3.3.7

Построим вектор c = (7, 5) . Перпендикулярно к нему прово-

дим линию уровня Z = 0 . Параллельным перемещением прямой Z = 0 в направлении вектора c находим точку С, в которой це-

23

левая функция достигает максимума (в точке С линия уровня находится в разрешающем положении). Решая совместно уравнения граничных прямых (1) и(2), находимкоординаты точкиС:

Таким образом, оптимальный план задачи X = (5,3) .

При этом Z max = Z(X ) = 7 5 +5 3 =50 .

Итак, по оптимальному плану следует выпускать 5 единиц продукции Ï 1 и 3 единицы продукции Ï 2 , что принесет при-

быль в 50 у.е.

Нетрудно заметить, что в задачах линейного программирования с двумя переменными экстремум достигается в вершине (крайней, угловой, точке) области допустимых решений. Это не случайный факт, и в n-мерном пространстве экстремум целевой функции в задачах линейного программирования достигается в крайней точке области допустимых решений (многогранника решений). Крайней (угловой) точкой выпуклого множества называют точку, которая не может быть представлена выпуклой линейной комбинацией двух других точек этого множества.

3.4. Свойства решений задач линейного программирования

Пусть задача линейного программирования имеет вид

n

Z = ∑c j x j (max); (3.4.1)

j=1

Пусть ранг r системы (3.4.2) меньше числа неизвестных n, т.е. r < n. Тогда, как известно, r переменных являются базисными, не ограничивая общности будем считать, что базисными переменными являются x1, ..., xr , а остальные n – r переменных –

свободными (xr +1, ..., xn ) . Если свободные переменные прирав-

24

нять к нулю, а базисные переменные при этом примут неотрицательные значения, то полученное частное решение системы (3.4.2) называется опорным решением. Если при этом хотя бы одна из базисных переменных равна нулю, то опорный план называется вырожденным опорным планом.

Теорема 3.4.1

Если ранг системы (3.4.2) равен r, то допустимый план X = (x1, x2 , ..., xr , 0, 0, ..., 0) является крайней точкой многогран-

ника планов.

Теорема 3.4.2 (основная теорема линейного программирования)

Если задача линейного программирования имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает того же значения в любой точке, являющейся их выпуклой линейной комбинацией.

3.5. Симплекс-метод решения задач линейного программирования

Симплекс-метод (С-метод) – это метод последовательного улучшения плана. В соответствии с основной теоремой линейного программирования целевая функция достигает своего экстремального значения в одной из крайних точек многогранника решений, поэтому, если найти какую-нибудь крайнюю точку многогранника решений, то можно перейти от нее к другой крайней точке, в которой значение целевой функции лучше (в смысле критерия оптимальности), чем в предыдущей. Продолжив целенаправленный перебор крайних точек, мы, в конце концов, найдем точку, в которой целевая функция примет экстремальное значение. Для этого нужно иметь признак того, что лучших крайних точек, чем полученная точка, нет. Согласно свойствам решений ЗЛП каждой крайней точке многогранника решений соответствует опорный план. Поэтому идея С-метода – в переходе от одного опорного плана к нехудшему (в смысле критерия оптимальности) опорному плану. Поскольку общее

25

число опорных планов не превышает Cnr , то через конечное

число шагов либо будет найден оптимальный опорный план, либо установлена неразрешимость задачи.

Решение ЗЛП С-методом складывается из двух этапов:

1)нахождение исходного опорного плана;

2)переход от исходного опорного плана к другому, более близкому к оптимальному, опорному плану, затем к следующему и так до тех пор, пока задача не будет решена.

С геометрической точки зрения перебор опорных планов можно толковать как переход по ребрам от одной вершины многогранника планов в другую по направлению к вершине, в которой целевая функция достигает экстремального значения.

На практике для решения задач С-методом используют С-таблицы (каждой таблице соответствует свое опорное решение). Рассмотрим задачу линейного программирования в канонической форме:

n

Z = ∑c j x j +c0 (min); (3.5.1)

j =1

Замечание: если ЗЛП задана в симметричной форме или в общем виде, ее следует преобразовать в каноническую форму, целевая функция должна быть на минимум.

Пусть ранг системы (3.5.2) равен r ( r ≤ m ) и x1, x2 , ..., xr − базисные переменные, остальные xr +1, ..., xn −свободные. Для того

чтобы решить задачу (3.5.1)–(3.5.3) с помощью С-таблиц, необходимо представить эту задачу в следующем виде:

Этот вид характеризуется следующими особенностями:

1)все ограничения системы (3.5.4) – уравнения, в уравнениях выделены базисные переменные (базисные переменные выражены через свободные неизвестные);

2)свободные члены системы (3.5.4) должны быть неотрицательны;

3)все переменные задачи x1, ... , xn – неотрицательны;

4)линейная форма Z, которую требуется минимизировать, должна быть выражена через свободные переменные и записана вместе с ними в левой части равенства.

Приведение задачи (3.5.1)–(3.5.3) к виду (3.5.4)–(3.5.7) рав-

носильно построению исходного опорного плана задачи. Действительно, придав свободным переменным нулевые значения, по-

лучим исходный опорный план X1 = (b1′,b2′, ..., br′, 0, ..., 0), при этом целевая функция Z примет значение, равное c0′ :

Z ( X1) = c0′ .

Вопрос о приведении задачи (3.5.1)–(3.5.3) к виду (3.5.4)– –(3.5.7) рассмотрим позднее.

Алгоритм С-метода

1.Систему ограничений и линейную форму задачи линейного программирования привести к виду (3.5.4)–(3.5.7).

2.Составить первую С-таблицу (табл. 3.5.1).

27

Таблица 3.5.1

Этой таблице соответствует исходный опорный план задачи линейного программирования:

X1 = (b1′,b2′, ..., br′, 0, ..., 0) , при этом Z1 = c0′ .

3. Просмотреть элементы последней строки табл. 3.5.1, соответствующей Z (элемент c0′ в рассмотрение не принимается).

Если среди них нет положительных, то опорное решение, соответствующее табл. 3.5.1, является оптимальным и минимумом

Z= c0′ .

4.Если в последней строке найдется хотя бы один положи-

тельный элемент, например c′j > 0 , то, отметив j-й столбец

стрелкой в верхней части табл. 3.5.1, перейти к п. 5.

5. Просмотреть элементы выделенного столбца над элементом c′j . Если среди них нет положительных, то минимум

Z→ −∞.

6.Если существует хотя бы один положительный элемент, то для положительных элементов отмеченного столбца вычис-

7. Выбрать наименьшее из этих отношений. Пусть оно достигается при k = i. Отметить i-ю строку стрелкой в левой части табл. 3.5.1. Объявить элемент aij′ , стоящий на пересечении вы-

деленных строки и столбца, разрешающим (ведущим). Его выделить квадратной скобкой.

8. Составить табл. 3.5.2. В базис на место xi поставить неизвестную x j . Разделить элементы отмеченной строки табл. 3.5.1 на разрешающий элемент aij′ и записать полученные

элементы в ту же строку табл. 3.5.2. Умножая отмеченную строку табл. 3.5.1 на соответствующие числа, прибавить ее к остальным строкам табл. 3.5.1 (метод Гаусса) с тем, чтобы получить выше и ниже разрешающего элемента aij′ нули. Все

вновь вычисленные элементы строк занести в табл. 3.5.2. Выписать новое опорное решение и соответствующее значение целевой функции.

9. С табл. 3.5.2 обратиться к п. 3.

Таблица 3.5.2

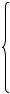
Пример 2

Решим задачу из примера 1 симплекс-методом (С-методом). Математическая модель задачи имеет вид

В соответствии с алгоритмом С-метода необходимо привести задачу к специальному виду. Сначала запишем систему ограничений задачи в каноническом виде, для этого введем четыре дополнительных неотрицательных переменных x3, x4 , x5, x6. То-

гда система (3.5.8) примет вид

Система (3.5.8) приобрела специальный вид (базисные переменные x3, x4 , x5 , x6 выражены через свободные переменные

x1 и x2 ). О том, как в общем случае привести систему ограни-

чений задачи к специальному виду, написано в п. 3.6. Преобразуем целевую функцию (3.5.10). Задачу об отыска-

нии максимума формы Z сведем к задаче об отыскании минимума формы Z1 = −Z : (−Z) = −7x1 −5x2 . Запишем полученное равенство в следующем виде:

−Z +7x1 +5x2 = 0 .

30