
Введение в математическое программирование
..pdf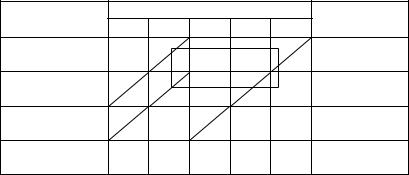
|
|
|
|
|
|
|
|
Таблица 3.8.10 |
|
Хранилище |
|
Потребители |
|
|
Запас |
||||
В1 |
В2 |
В3 |
В4 |
В5 |
топлива, т |
||||
|
|||||||||
А1 |
5 |
2 + |
60 |
3 |
6 |
0– |
10 |
70 |
|
|
4 |
3 – |
|
7 |
|
|
|||
А2 |
|
5 |
+ |
|
90 |
||||
40 |
|
10 |
40 |
0 |
|||||
|
|
|
|
|
|
||||
А3 |
2 |
4 |
|
1 |
5 |
0 |
|
50 |
|
10 |
|
40 |
|
||||||
Потребность |
|
|
|
|
|
|
|||
50 |
70 |
40 |
40 |
10 |
210 |
||||
в топливе, т |
|
|
|
|
|
|
|
|
|
В результате распределения топлива по потребителям получили невырожденный план: условие для занятых клеток m +n −1 =3 +5 −1 = 7 выполняется.
Определяем потенциалы:
u1 = 0; v2 = 2; v5 = 0; u2 =1; v4 = 6; v1 =3; u3 = −1; v3 = 2.
Вычислим оценки свободных клеток:
S11 =5 −(0 +3) = 2,
S13 =3 −(0 + 2) =1,
S14 = 6 −(0 +6) = 0,
S23 =5 −(1+2) = 2, S25 = 0 −(0 +1) = −1(!), S32 = 4 −(2 −1) =3, S34 =5 −(6 −1) = 0, S35 = 0 −(0 −1) =1.
Среди оценок есть одна отрицательная (S25 = −1) , следова-
тельно, план перевозки можно улучшить, загрузив соответствующую свободную клетку. Построим для нее цикл пересчета, покажем его в табл. 3.8.10 штриховой линией.
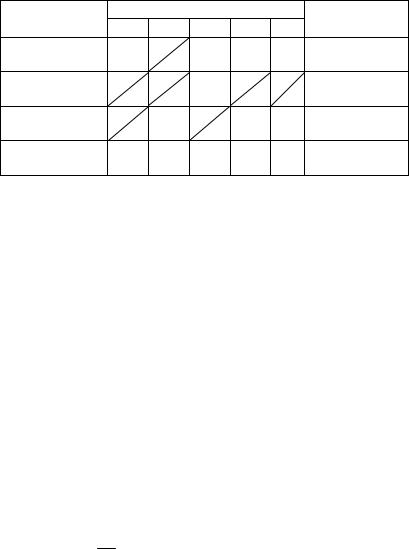
Наименьшее количество топлива в отрицательных вершинах цикла равно 10 т. После смещения по циклу 10 т топлива получаем новый план перевозок (табл. 3.8.11).
71
|
|
|
|
|
|
Таблица 3.8.11 |
|
Хранилище |
|
Потребители |
|
Запас |
|||
В1 |
В2 |
В3 |
В4 |
В5 |
топлива, т |
||
|
|||||||
А1 |
5 |
2 |
3 |
6 |
0 |
70 |
|
70 |
|||||||
|
|
|
|
|
|
||
А2 |
4 |
3 |
5 |
7 |
0 |
90 |
|
40 |
0 |
40 |
10 |
||||
|
|
|
|||||
А3 |
2 |
4 |
1 |
5 |
0 |
50 |
|
10 |
40 |
||||||
Потребность |
|
|
|
|
|||
50 |
70 |
40 |
40 |
10 |
210 |
||
в топливе, т |
|
|
|
|
|
|
|
Полученный план является вырожденным. Поставим чис- |
|||||||
ло 0 в одну из свободных клеток и будем считать ее занятой. |
|||||||
Положим õ22 = 0 . |
|
|
|
|
|
||
Вычислим потенциалы: |
|
|
|
|
|||
u1 = −1; u2 = 0; u3 = −2; v1 = 4; v2 = 3; v3 = 3; v4 = 7; v5 = 0 .
Найдем оценки свободных клеток:
S11 = 2, S13 =1, S14 = 0, S15 =1, S23 = 2, S32 =3, S34 = 0, S35 = 2.
Все оценки Sij ≥ 0, следовательно, получен оптимальный
план задачи. Поскольку среди оценок есть нулевые, то оптимальный план не является единственным (случай бесчисленного множества оптимальных планов).
Итак, выписываем оптимальный план задачи
|
0 |
70 |
0 |
0 |
|
|
|
Х* = |
|
40 |
0 |
0 |
40 |
|
, |
|
|
||||||
|
|
10 |
0 |
40 |
0 |
|
|
|
|
|
|
||||
вычисляем экстремальное значение целевой функции
Z*min = Z( X * ) = 2 70 +4 40 +7 40 + 2 10 +1 40 = 640.
Десять тонн топлива, находящегося в хранилище А2, осталось нераспределенным.
72
Транспортная задача в сетевой постановке
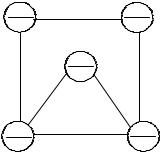
Пусть условия ТЗ заданы в виде картосхемы, т.е. пункты отправления и назначения грузов изображены в виде кружков, соединенных дугами (рис. 3.8.1). Эти дуги указывают дороги, которые связывают поставщиков
и потребителей. |
На картосхеме |
III |
2 |
I |
|
приводятся и другие показатели, |
–20 |
|
30 |
||
|
|
|
|||
относящиеся к общей постановке |
|
|
|
||
задачи (величины запасов груза |
4 |
II |
6 |
||
и потребностей в нем, величины |
70 |
||||
|
|
||||
|
|
|
|||
ñij , являющиеся |
показателями |
|
3 |
5 |
|
принятого в задаче критерия оп- |
|
||||
|
|
|
|||
тимальности (тарифы, расстояние |
IV |
1 |
V |
||
и т.п.)). Такую постановку ТЗ |
–40 |
|
–40 |
||
|
|
|
|||
будем называть сетевой. |
|
Рис. 3.8.1 |
|||
Кружки, изображенные на |
|
|
|
||
рис. 3.8.1, будем называть вершинами, отрезки прямых, изображающие участки дорог между пунктами – ребрами (звеньями, дугами) сети.
Пункты отправления и назначения обозначаем римскими цифрами. Запас каждого пункта отправления обозначаем положительной величиной, а потребность – отрицательной. На рис. 3.8.1 имеем два пункта отправления (I, II), в которых сосредоточено 30 и 70 единиц груза соответственно, и три пункта назначения (III, IV, V), спрос которых равен 20, 40, 40 единиц груза соответственно.
Таким образом, имеем закрытую модель ТЗ в сетевой постановке.
Картосхему можно представить и без учета масштаба, при этом на картосхему выносят и такие вершины, которые не являютсяпересечениямидуг, атакжепоставщикамиипотребителями.
Наличие таких вершин не повлияет на способ решения, если считать, что запасы (потребности) груза в них равны нулю. Такие вершины называют нулевыми.
Различия между ТЗ в матричной и сетевой формах незначительны, так как методы их решения основаны на одних и тех же идеях. Далее будем использовать уже известный метод потенциалов. Решение задачи на сети начинается с построения начального опорного плана.
73
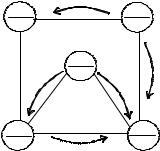
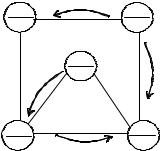
Последовательность решения задачи рассмотрим на конкретном примере (см. рис. 3.8.1). Поставки груза из вершины в вершину будем обозначать стрелками с указанием величины поставок.
Опорныйпландолженудовлетворятьследующимтребованиям:
1)все запасы должны быть распределены, а потребности удовлетворены;
2)к каждой вершине должна подходить или выходить из нее хотя бы одна стрелка;
3)общее количество стрелок должно быть на единицу
|
|
|
|
меньше числа вершин; |
|
|
[2] |
20 |
|
[0] |
4) стрелки не должны обра- |
||
III |
|
|
I |
зовывать замкнутый контур. |
||
–20 |
|
|
30 |
|||
2 |
|
План |
распределения груза |
|||
|
|
|
||||
|
[1] |
|
|
(рис. 3.8.2) отвечает этим тре- |
||
4 |
II |
6 |
10 |
бованиям. |
|
|
|
70 |
|
|
Далее |
следует |
проверить |
40 |
|
30 |
|
|||
|
|
план на оптимальность. |
||||
3 |
5 |
|
|
|||
|
|
Для этого вычислим потен- |
||||
|
|
|
|
|||
IV |
1 |
|
V |
циалы. Однойизвершин(например |
||
–40 |
|
|
–40 |
вершине I) присвоим |
некоторое |
|
[4] |
|
|
[6] |
|||
|
Рис. 3.8.2 |
|
|
значение |
потенциала |
(например |
|
|
|
равное нулю). Для наглядности |
|||
|
|
|
|
|||
потенциалы будем заключать в рамки. После этого, двигаясь по стрелкам, определим потенциалы остальных вершин, руководствуясь правилом: если стрелка выходит из вершины, то к по-
тенциалу этой вершины прибавим показатель ñij критерия оптимальности, если же направление стрелки противоположно, то ñij
вычтем.
В нашем примере потенциал вершины III: 0 + 2 = 2 (стрелка выходит из вершины I); потенциал вершины V: 0 + 6 = 6; потенциал вершины II: 6 – 5 = 1 (стрелка входит в вершину V); потенциал вершины IV: 1 + 3 = 4.
После вычисления потенциалов находят характеристики ребер без стрелок по правилу: из большего потенциала вычитается
меньший, а разность вычитается из показателя ñij , отвечающего
данному ребру. Если все ребра без стрелок имеют неотрицательные характеристики, то составленный план является оптимальным.
74
Вычислим характеристики ребер без стрелок в нашем приме-
ре: S34 = 4 −(4 −2) = 2 ; S45 =1−(6 −4) = −1 . Итак, ребро IV–V об-
ладаетотрицательнойхарактеристикой. Значит, планнеоптимален. Для улучшения плана надо «загрузить» то ребро без стрелки, которому соответствует отрицательная характеристика. Если таких ребер несколько, то выбирается ребро с наибольшей по абсолютной величине отрицательной характеристикой и к нему подрисовывается новая стрелка. При этом образуется замкнутый контур из стрелок. Новая стрелка направляется от вершины
сменьшим потенциалом к вершине с большим потенциалом.
Внашем примере новая стрелка направлена от вершины IV
квершине V (на рис. 3.8.2 она показана штриховой линией). Для определения величины поставки для «загружаемого» ребра рассматриваются все стрелки образовавшегося контура (если на сети – опорный план, то такой контур всегда существует и причем только один), имеющие направление, противоположное направлению новой стрелки, и среди них находится стрелка с наименьшей по-
ставкой λ.
Выбранная таким образом величина прибавляется по всем поставкам в стрелках, имеющих то же направление, что и новая стрелка, и вычитается из поставок в стрелках, имеющих проти-
воположное направление. По- |
[7] |
|
20 |
|
[5] |
||
ставки в стрелках, не входящих |
III |
I |
|||||
в контур, сохраняются неиз- |
|
–20 |
2 |
30 |
|
||
|
|
|
|
||||
менными. Стрелка, по которой |
|
|
[7] |
|
|
||
выбрано число λ, ликвидирует- |
|
4 |
II |
6 |
10 |
||
ся, и общее число стрелок оста- |
|
|
70 |
|
|
||
|
70 |
|
|
|
|||
ется прежним. |
|
|
|
|
|
||
|
|
3 |
5 |
|
|
||
Преобразованный описан- |
|
|
|
||||
|
|
|
|
|
|||
ным способом |
опорный план |
|
IV |
1 |
V |
|
|
приведен на рис. 3.8.3. |
[10] |
–40 |
30 |
–40 |
[11] |
||
Новый опорный план ис- |
|
|
Рис. 3.8.3 |
|
|
||
следуется |
на |
оптимальность |
|
|
|
|
|
подобно |
предыдущему. Практически удобней вести |
расчеты |
|||||
с положительными числами, поэтому значение первого (выбираемого произвольно) потенциала лучше брать равным не нулю, а какому-либо положительному числу. Пусть потенциал верши-
75

ны IV равен, например, 10, тогда после вычисления остальных потенциалов для ребер без стрелок получим следующие характеристики: S34 = 4 −(10 −7)=1 ; S25 = 5 −(11−7)=1 . Они положительны, значит, опорный план на рис. 3.8.3 оптимален.
Определим значение целевой функции:
Zmin = 20 2 +10 6 +30 1+70 3 =340 .
Замечание:
Вырождение плана ТЗ в сетевой постановке внешне проявляется в том, что при полном использовании запасов и полном удовлетворении потребностей количество стрелок оказывается меньше, чем n −1 , гдеn – общее числовершин(включая инулевые).
Способ преодоления вырождения весьма прост: дополнительно вводится нужное количество стрелок с нулевыми поставками. Направления стрелок выбираются произвольно, однако они не должны образовывать замкнутый контур. В случае открытой модели ТЗ вводят фиктивного потребителя (поставщика) со спросом, равным небалансу. Фиктивный потребитель (поставщик) соединяется ребрами непосредственно со всеми поставщиками (потребителями). При этом показатели ñij ребер,
соединяющих фиктивного потребителя (поставщика) с поставщиками (потребителями), следует брать одинаковыми и сравнительно большими.
Делается так для того, чтобы исключить возможность использования фиктивной вершины в качестве промежуточного пункта.
3.9.Задача о назначении
Вобщем виде задача о назначении формулируется следующим образом:
Имеется n работ и n кандидатов для их выполнения. Затра-
ты i-го кандидата на выполнение j-й работы равны ñij
(i =1, n; j =1, n) . Каждый кандидат может быть назначен только
на одну работу, и каждая работа может быть выполнена только одним кандидатом. Требуется найти назначение кандидатов на работы, при котором суммарные затраты на выполнение работ минимальны.
76

Составим математическую модель задачи.
Пусть xij – переменная, значение которой равно 1, если i-й
кандидат выполняет j-ю работу, и 0 – в противном случае (такие переменные называют булевыми). Тогда условие о том, что каждый кандидат выполняет только одну работу, запишется в виде
n
∑xij =1 ( j =1, n) .
i=1
Условие о том, что каждая работа может выполняться одним кандидатом, запишется в виде
n
∑xij =1 (i =1, n) .
j=1
Целевая функция задачи имеет вид
n n
Z= ∑ ∑cij xij .
i=1 j=1
Вфункцию входят только те значения cij , для которых xij
отличны от 0, т.е. входят затраты, соответствующие назначенным работам.
Итак, математическая модель выглядит следующимобразом:
n n |
(min); |
|
Z = ∑ ∑cij xij |
(3.9.1) |
|
i=1 j=1 |
|
|
|
n |
|
|
|
|
|
|
||
|
|
||||||||
|
∑xij =1 (i =1, n), |
||||||||
j =1 |
|||||||||
n |
|
|
|
|
|
|
|
||
|
|
|
|||||||
∑xij =1 ( j =1, n), |
|||||||||
i=1 |
|||||||||
x {0,1} (i = |
|
; j = |
|
). |
|||||
1, n |
1, n |
||||||||
|
ij |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решить задачу о назначении – значит найти
(3.9.2)
(3.9.3)
(3.9.4)
õij , удовлетво-
ряющие условиям (3.9.2)–(3.9.4) и доставляющие минимум функции (3.9.1). Задача (3.9.1)–(3.9.4) является задачей линейно-
77
го программирования (целевая функция линейна, ограничения линейны) и может быть решена С-методом. Также задача (3.9.1)–(3.9.4) – это транспортная задача, в которой правые части ограничений равны 1, а переменные могут принимать только два значения. Однако с учетом специфики задачи для ее решения разработаны специальные методы, один из которых – венгерский.
Венгерский метод решения задачи о назначении
Для решения задачи о назначении составляют табл. 3.9.1. В первом столбце записаны номера кандидатов, в первой
строке – номера работ. На пересечении i-й строки и j-го столбца стоят затраты ñij на выполнение i-м кандидатом j-й работы
(в качестве ñij можно рассматривать полезность, связанную с выполнением i-м исполнителем j-й работы).
Таблица 3.9.1
Номер кандидата |
|
|
Номер работы |
|
|||
1 |
2 |
|
… |
j |
… |
n |
|
1 |
ñ |
ñ |
|
… |
ñ1 j |
… |
ñ |
|
11 |
12 |
|
|
|
|
1n |
2 |
ñ21 |
ñ22 |
|
… |
ñ2 j |
… |
ñ2n |
… |
… |
… |
|
… |
… |
… |
… |
i |
ñi1 |
ñi2 |
|
… |
ñij |
… |
ñin |
… |
… |
… |
|
… |
… |
… |
… |
n |
ñn1 |
ñn2 |
|
… |
ñnj |
… |
ñnn |
В венгерском методе используется следующий принцип: оптимальность решения задачи о назначении не нарушается при уменьшении (увеличении) элементов строки (столбца) на одну и ту же величину.
Решение считается оптимальным, если все измененные таким образом затраты ñij′ ≥ 0 и можно отыскать такой набор xij ,
что
n n
∑∑cij′ xij = 0 .
i=1 j=1
78
Алгоритм венгерского метода решения задачи о назначении
1.Получаем нули в каждой строке. Для этого в каждой строке определяем наименьший элемент и его значение отнимаем от всех элементов этой строки.
2.Получаем нули в каждом столбце. В преобразованной таблице в каждом столбце определяем минимальный элемент
иего значение вычитаем из всех элементов этого столбца.
3.Поиск оптимального решения. Просматриваем строку, содержащую наименьшее число нулей. Отмечаем один из нулей
этой строки и зачеркиваем все остальные нули этой строки и того столбца, в котором находится отмеченный нуль. Аналогичные операции последовательно проводим для всех строк. Если назначение, которое получено при всех отмеченных нулях, является полным (т.е. число отмеченных нулей равно n), то решение является оптимальным. В противном случае следует перейти к п. 4.
4. Поиск минимального набора строк и столбцов, содержащих все нули. Для этого необходимо отметить:
1)все строки, в которых не имеется ни одного отмеченного нуля;
2)все столбцы, содержащие перечеркнутый нуль хотя бы
водной из отмеченных строк;
3)все строки, содержащие отмеченные нули хотя бы в одном из отмеченных столбцов.
Действия 2 и 3 повторяются поочередно до тех пор, пока есть что отмечать. После этого необходимо зачеркнуть каждую непомеченную строку и каждый помеченный столбец.
Цель этого этапа – провести минимальное число горизонтальных и вертикальных прямых, пересекающих по крайней мере один раз все нули.
5.Перестановка некоторых нулей. Взять наименьшее число из тех клеток, через которые не проведены прямые. Вычесть его из каждого числа, стоящего в невычеркнутых столбцах, и прибавить к каждому числу, стоящему в вычеркнутых строках. Эта операция не изменит оптимального решения, после чего весь цикл расчета повторить, начиная с п. 3.
79
Пример 11
Институт получил гранты на выполнение четырех исследовательских проектов. Выходные результаты первого проекта являются входными данными для второго проекта, выходные результаты второго проекта – это входные данные для третьего проекта, результаты третьего проекта используются для работы над четвертым проектом. В качестве научных руководителей проектов рассматриваются кандидатуры четырех ученых, обладающих различным опытом и способностями. Каждый ученый оценил время, необходимое ему для реализации проекта.
Задана матрица времен:
3 |
7 |
5 |
8 |
|
|
|
2 |
4 |
4 |
|
|
|
5 |
||||
Ò = |
4 |
7 |
2 |
8 |
. |
|
|
||||
|
9 |
7 |
3 |
8 |
|
|
|
||||
В i-й строке и j-м столбце матрицы Т стоит время на выполнение i-м ученым j-го проекта. Продолжительность времени задана в месяцах.
Требуется выбрать научного руководителя для выполнения каждого проекта так, чтобы суммарное время выполнения всех проектов было минимальным.
Решение
Данная задача, очевидно, является задачей о назначении. В качестве работ рассматриваются исследовательские проекты, в качестве кандидатов – ученые, претендующие на роль научных руководителей.
Введем переменные
1, если i-й ученый – научный руководитель j-го проекта, xij = 0, в противном случае.
Целевая функция задачи имеет вид
Z=3x11 +7x12 +5x13 +8x14 +2x21 + 4x22 +4x23 +5x24 +
+4x31 +7x32 + 2x33 +8x34 +9x41 +7x42 +3x43 +8x44 (min).
80
