Прочность и разрушение материалов

Рис. 2.10. R-кривая (ПНС)

Пусть трещина размера li нагружена напряжением 1. Если длина трещины увеличится до величины l1 li l1, то коли-

чество выделенной при этом энергии будет задано точкой А, при дальнейшем увеличении её длины при постоянном напряжении G будет увеличиваться по линии АС. Увеличение напряжения до

ном напряжении G будет изменяться от B к Н. Наконец, при напряжении c длина трещины становится равной lс, а величины G и R доходят до точки D. Рост трещины при постоянном напряжении c сопровождается увеличением G по линии DF. Эта

линия лежит выше кривой. Поскольку G остается большим, чем R, происходитокончательноеразрушение в точке D, в которой

Уравнение (2.11), очевидно, представляет собой энергетический критерий для разрушения при ПНС.

Рис. 2.11. Инвариантная R-кривая

Инвариантность R-кривой. Крафт и другие14 сделали предположение, что R-кривая инвариантна: она имеет одинаковый вид безотносительно к начальному размеру трещины. Это означает, что условие разрушения для трещин произвольных размеров следует из графического построения, которое выполнено на рис. 2.11, где касательные для различных длин трещин проведе- ныкединственнойR-кривой.

2.7. J-интеграл

До сих пор предполагалось, что зона пластичности при вершине трещины настолько мала, что применима теория упругости. Если это так, то пластические деформации при вершине трещины не оказывают влияния на интенсивность выделения энергии и величина G определяется упругим полем напряжений.

14 Krafft J.M., Sullivan A.M., Boyle R.W. Effect of dimensions on fast fracture instability of notched sheets // Proc. of the crack-propagation symposium, Cranfield. – 1961. – Vol. I. – P. 8–28.

62

Можно показать, что если зону пластичности при вершине трещины не считать пренебрежимо малой, то она будет оказывать влияние на интенсивность выделенияэнергии.

Рис. 2.12. Определение J-интеграла

Для того чтобы точно вычислить влияние пластических деформаций на величину G, нужно получить точное решение упругопластической задачи о поле напряжений при вершине трещины. Существует косвенный метод, в основе которого лежит J-интеграл, определяемый выражением

где Г – замкнутый контур, который нужно обойти против часовой стрелки, окружающий в напряжённом твёрдом теле некоторую область (рис. 2.12);

Т – вектор напряжений, перпендикулярный контуру Г и направленный во внешнюю сторону, Ti ijnj ;

и– перемещениевнаправленииосих; ds – элементконтураГ.

Крометого, энергиядеформацийединицыобъёма

W W x, y W ij d ij .

0

Можно показать15, что еслиГ– замкнутыйконтур, тоJ = 0.

15 Rice J.R. A path independent integral and the approximate analysis of strain concentrations by notches and cracks // J. Appl. Mech. – 1968. – Vol. 35. – P. 379–386.

63

Характерной особенностью J-интеграла является его независимость от формы и размеров контура Г (контур может быть как очень малым, так и совпадать с границей тела). Контур Г может оказаться внутри пластической зоны, пересекать её или быть вне её – во всех случаях значение J-интеграла остаётся неизменным.

Рассмотрим замкнутый контур ABCDEFA вокруг вершины трещины (рис. 2.13, а). Интеграл по этому контуру равен нулю. Поскольку на частях берегов трещины CD и AF значения T = 0 иdy = 0, их вклад в интеграл равен нулю. Поэтому интеграл по контуру ABC должен быть равен интегралу по контуру DEF (с обратным знаком). Это означает, что, независимо от того, берётся ли J-интеграл по контуру ABC или FED, результат будет один итот же: интеграл не зависит от пути интегрирования, т.е. JГ1 = JГ2 (рис. 2.13, б). Необходимо обратить внимание на то, что этот интеграл, не зависящий от пути интегрирования, берётся не по замкнутомуконтуру: пределыинтегрированиялежатнакраях трещины.

Рис. 2.13. Контур обхода вершины трещины

Для упругого случая J-интеграл можно вычислить, используя решение упругой задачи о поле напряжений. Отсюда следует, что

64

Вычисление интеграла (2.12) приводит к соотношению

Совершенно очевидно, что для упругого случая J-интеграл эквивалентен интенсивности выделения энергии. Райc также показал, что

где П – потенциальная энергия. В упругом случае уравнения

(2.13) и (2.14) эквивалентны.

Другими словами, J есть обобщённая функция выделения энергии за счёт распространения трещины; эта функция может быть также справедлива в том случае, когда вблизи вершины трещины имеются значительные пластические деформации. Поскольку J-интеграл не зависит от пути интегрирования, его можно определить менее сложным путём, выбирая путь интегрирования, вдоль которого интегрирование можно выполнить достаточно просто (т.е. вдоль краёв образца). Таким образом, интеграл дает возможность сравнительно просто определять интенсивность выделения энергии для случая, когда при вершине трещины имеется большая зона пластичности. Можно ожидать, что существует критическое значение JIс, при котором может начаться рост трещины. Это должно иметь силу и в упругом

Уравнение (2.15) утверждает, что процесс роста трещины, связанный с большими пластическими деформациями, можно определить из JIс, зная значение GIс, которое было определено для случая, когда пластическими деформациями можно пренебречь, инаоборот.

Согласно уравнению (2.14), J-интеграл можно найти из диаграммы «нагрузка – перемещение», точно так же как и в упругом случае, определяя податливость образца. Отличие заключа-

65

ется в том, что в результате пластичности на диаграмме «нагрузка – перемещение» может иметь место нелинейный участок. Этот факт схематически отображен на рис. 2.14. Площадь между двумя кривыми, связывающими нагрузку с перемещением для

трещин, имеющих размеры l и l + dl, равна Vl dl, т.е. эта пло-

щадь равна J.

Кривые, связывающие нагрузки и перемещения в образце, можно получить экспериментально, последовательно увеличивая размер трещины, а площадь между двумя кривыми для трещин с мало отличающимися размерами – определить графически. Полученные таким образом значения J можно построить как функцию перемещения v. Определяя значение v при разрушении для трещин различных размеров, из рисунка можно выяснить, происходит ли разрушение во всех случаях при одинаковом значении J.

Подобные эксперименты были выполнены Биглеем и Лэндисом16; некоторые из результатов экспериментов пред-

16 Begley J.A., Landes J.D. The J-integral as a fracture criterion // Proc. Natl. Symp. Fracture Mechanics, Part I. ASTM STP. – 1972. – Vol. 514. – P. 1–20; Landes J.D., Begley J.A. The effect of specimen geometry on JIc, fracture toughness // Proc. Natl. Symp. Fracture Mechanics, Part II; ASTM STP. – 1972. – Vol. 514. – P. 24–39.

66

ставлены на рис. 2.15. Они обнаружили, что разрушение действительно происходит при постоянном значении JIс, которое было равно GIс, определённой независимо.

При использовании J-интеграла требование ограниченности пластических деформаций можно опустить. Вообще говоря, это позволяет определять JIс (а также, следовательно, GIс) из испытаний образца малых размеров.

Метод представляется наиболее многообещающим в тех случаях, когда возникают большие пластические деформации (т.е. при плоской деформации). Однако в этих случаях перед разрушением идёт медленный рост трещины. В процессе медленного роста трещины за её вершиной происходит разгрузка материала. До сих пор независимость J-интеграла от пути интегрирования была доказана только при использовании теории пластических деформаций, которая не предусматривает разгрузку материала. Поэтому в настоящее время критерий разрушения, основанный на использовании J-интеграла, следует применять лишь к процессу зарождения трещин. Кроме того, до сих пор не существует методики использования J-интеграла для описания процесса стабильного роста трещины.

2.8. Скорость распространения трещины

Нестабильность, предшествующая разрушению, возникает тогда, когда при расширении трещины интенсивность выделения энергии упругих деформаций G постоянно превышает сопротивление росту трещины R. Разница между G и R определяет количество энергии, которое может перейти в кинетическую; следовательно, эта величина задает скорость, с которой эта трещина будет распространяться в среде. Следовательно, общее количество энергии, которое может перейти в кинетическую энергию, после того как размер трещины увеличится на l, определя-

67

ется интегралом от разности (G – R) на отрезке l. Этот интеграл представлен на рис. 2.16 заштрихованной областью. Изображённый на рис. 2.16 случай основан на трёх упрощающих предположениях:

1.процесс распространения трещины происходит при постоянном напряжении;

2.интенсивность выделения энергии упругих деформаций не зависит от скорости распространения трещины;

3.сопротивление росту трещины постоянно.

Рис. 2.16. Графическое представление кинетической энергии: 1 – R-кривая для материалов, свойства которых зависят от скорости деформирования

Материалы, свойства которых зависят от скорости деформирования, имеют убывающую R-кривую, показанную на рис. 2.16 штриховойлинией.

Теория Мотта17

Мотт рассмотрел задачу о распространении трещины в бесконечной пластинке, подвергающейся не зависящему от времени одноосному растяжению перпендикулярно к плоскости

17 Mott N.F. Fracture of metals: theoretical considerations // Engineering. – 1948. – Vol. 165. – P. 16–18.

68

Он предположил, что поля напряжений и смещений в динамическом случае те же самые, что и в упругом статическом случае, при той же самой длине трещины. Поэтому, если u и v – компоненты смещения, а l(t) – полудлина трещины и dl/dt мало, по сравнению со скоростью волны сдвига в материале, компоненты скорости в данной точке пластинки можно записать в виде:

du u l , dt l t

dv v l . dt l t

Кинетическая энергия для пластины единичной толщины

где – плотность на единицу толщины.

Мотт показал, что так как u и v пропорциональны l E , тоu l и v l будут пропорциональны E. В случае беско-

нечной пластины размер трещины l является единственным характерным размером, имеющим размерность длины. Подразумевая, что область интегрирования S занимает всю плоскость, приходим к выводу, что поверхностный интеграл в уравнении (2.16) будет пропорционален l2. Это означает, что результат интегрирования может быть пропорционален kl2, где k – константа, и может зависеть только от коэффициента Пуассона . Следовательно, уравнение (2.16) можно записать в виде

Кинетическая энергия пропорциональна квадратам размера трещины и напряжения. Совершенно очевидно, что она должна быть пропорциональна удельной массе и квадрату скорости

69

распространения трещины. Используя рис. 2.15, можно получить другое выражение для кинетической энергии:

Рассматривая случай, когда R – константа, а величина G при постоянном напряжении определяется решением статической задачи, получаем выражение для кинетическойэнергии

Константа R в начале нестабильного процесса равна GIс (величина которого задана соотношением GIc E2lc . Подстав-

ляя в соотношение (2.19) равенство R= GIс и проводя интегрирование, получаем (для двух вершин трещины)

Два выражения (2.17) и (2.20) для кинетической энергии можно приравнять друг к другу, получив

Выражение E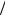 есть скорость продольных волн в среде, т.е. оно равно скорости звука vs . Таким образом, при l lc скорость трещины будет приближаться к предельной скорости

Теперь задача сводится к оценке постоянной k, для определения которого Робертс и Уэллс18 оценили численно интеграл, входящий в уравнение (2.16), и построили график зависимости

18 Roberts D.K., Wells A.A. The velocity of brittle fractures // Engineering. – 1954. – Vol. 178. – P. 820.

70