Анализ и синтез одноконтурных систем автоматического регулирования т

цией, позволяют устойчиво и без остаточной неравномерности регулировать работу большого числа промышленных объектов. По этой причине они получили широкое распространение на практике.

9. Определение оптимальных настроек регуляторов

Регулятор, включенный в АСР (см. рис. 1), может иметь несколько настроек (Kр, Ти и др.), каждая из которых может изменяться в достаточно широких пределах. При определенных значениях параметров настроек регулятора система будет управлять объектом в соответствии с технологическими требованиями, при других – может привести к неустойчивой работе системы регулирования. Поэтому возникает задача определения настроек регулятора, соответствующих устойчивой системе, и выбора из них оптимальных.

Оптимальными настройками регулятора называются настройки, которые соответствуют минимуму (или максимуму) какого-либо показателя качества. Требования к показателям качества устанавливаются непосредственно, исходя из технологических требований.

51

Для быстрой и приближенной оценки значений настроек регуляторов используется формульный метод. Если объект управления представляет собой инерционное звено первого порядка с запаздыванием, т.е. описывается передаточной функцией

где Kоб – коэффициент передачи объекта; Тоб – постоянная времени объекта; зап – запаздывание объекта, то настройки П-, ПИ- и ПИДрегуляторов могут быть определены по приведенным в табл. 1 формулам в зависимости от того, какой вид переходного процесса требуется получить. Во второй колонке табл. 1 приведены формулы

52

для апериодического процесса без перерегулирования, в третьей – с перерегулированием 20 %, в четвертой – для процесса с максимальным быстродействием (данный процесс может быть сильно колебательным).

10. Устойчивость

Под устойчивостью понимают способность САУ восстанавливать свое состояние равновесия после устранения возмущающего воздействия. Различают три типа систем:

а) устойчивые системы после устранения возмущающего воздействия возвращаются в исходное состояние равновесия; в результате ступенчатого возмущающего воздействия устойчивая система или апериодически, или совершая затухающие колебания, переходит в новое состояние равновесия (рис. 19, а);

б) неустойчивые системы после устранения возмущающего воздействия апериодически удаляются от состояния равновесия или начинают совершать расходящиеся колебания; переходные характеристики неустойчивых систем показаны на рис. 19, б;

в) нейтральные системы после устранения возмущающего воздействия или приходят в состояние равновесия, отличающееся от исходного, или совершают незатухающие колебания; одна из возможных переходных характеристик нейтральной системы показана на рис. 19, в.

Устойчивость является одним из главных требований, предъявляемых к САР, поскольку определяет ее работоспособность. Иначе говоря, неустойчивая система принципиально неработоспособна.

а б в

Рис. 19. Переходные процессы: а – система устойчива; б – система не устойчива; в – система на границе устойчивости

53

Также существуют такие понятия, как граница устойчивости и устойчивость в малом, которые можно рассмотреть на примере системы, состоящей из шара и различного вида поверхностей (рис. 20). САР может быть устойчива «в малом», но неустойчива «в большом». Примером такой системы может служить средний шар системы, изображенной на рис. 20, г). Систему, находящуюся на границе устойчивости иллюстрируют крайние шары на рис. 20, г.

аб

вг

Рис. 20. Устойчивость систем: а – система устойчива;

б– нейтральная система; в – система не устойчива;

г– система устойчива в малом

Для того чтобы определить устойчивость системы или какоголибо ее элемента, используются критерии устойчивости.

Все приведенные ниже критерии справедливы для определения устойчивости как САР, так и отдельных ее элементов.

10.1. Корневой критерий устойчивости

Данный критерий является необходимым и достаточным критерием устойчивости и формулируется следующим образом: линей-

ная САР устойчива, если все корни характеристического уравнения САР лежат в левой полуплоскости; если хотя бы один корень находится на мнимой оси, то говорят, что САР находится на границе устойчивости; если хотя бы один корень находится в правой полуплоскости, то САР является неустойчивой.

54

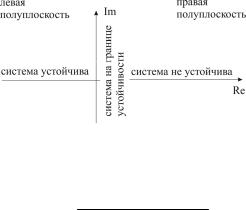
Иными словами, все действительные корни и действительные части комплексных корней характеристического уравнения САР должны быть отрицательны. В противном случае САР неустойчива

(рис. 21).

Рис. 21. Устойчивость систем

Пример 7. Передаточная функция системы имеет вид

W ( p) 3 23 p 4 . p 2 p 2,25 p 1,25

Определить устойчивость системы по корневому критерию.

Р е ш е н и е

Характеристическое уравнение системы имеет вид p3 2 p2 2,25 p 1,25 0 .

Данное характеристическое уравнение имеет три корня p1 = –1, p2 = –0,5 + j, p3= –0,5 – j.

Действительные части всех корней отрицательны (т.е. корни лежат в левой полуплоскости), следовательно, система устойчива.

10.2. Алгебраические критерии устойчивости

10.2.1. Критерий Стодолы

Данный критерий – следствие из предыдущего и является необходимым, но недостаточным. Критерий Стодолы формулируется следующим образом: линейная САР устойчива, если все коэффициенты ее характеристического уравнения положительны.

55

10.2.2. Критерий Гурвица

Критерий Гурвица формулируется следующим образом: для того чтобы линейная система была устойчива, необходимо и достаточно, чтобы все диагональные миноры матрицы Гурвица порядка n – 1 были положительны.

Пустьхарактеристическоеуравнениелинейнойсистемыимеетвид an pn an 1 pn 1 ... a2 p2 a1 p a0 0 ,

тогда матрица Гурвица будет иметь вид

В главной диагонали данной матрицы расположены по порядку коэффициенты от an–1 до a0. В строках относительно главной диагонали коэффициенты располагаются через один: слева увеличиваясь, справа – уменьшаясь.

Все диагональные миноры образуются из приведенного детерминанта последовательным вычеркиванием последних строки и столбца предыдущих миноров:

1 an 1 ,

…

56

Пример 8. Передаточная функция разомкнутой САР

Wpc ( p) 2 p3 4 9 p2 3 6 p2 1 .

2 p 3 p p

Определить устойчивость замкнутой системы по критерию Гурвица.

Р е ш е н и е

Определим характеристическое уравнение замкнутой системы (см. пример 6):

D(р) = A(р) + B(р) =

=(2р4 + 3р3 + р2) + (2р3 + 9р2 + 6р + 1) =

=2р4 + 5р3 + 10р2 + 6р + 1.

Поскольку степень характеристического уравнения замкнутой системы n = 4, то матрица Гурвица будет иметь размерность 4×4. Коэффициенты характеристического уравнения замкнутой: а4 = 2,

а3 = 5, а2 = 10, а1 = 6, а0 = 1.

Матрица Гурвица для замкнутой системы имеет вид

Определители (диагональные миноры матрицы) имеют вид:

1 = 5 > 0,

57

(0 10 0 5 5 1 2 6 6) 203 0,

Поскольку все определители матрицы Гурвица положительны, то САР устойчива.

10.2.3. Критерий Льенара – Шипара

Критерий Льенара – Шипара является упрощенным критерием Гурвица и формулируется следующим образом: если все коэффици-

енты характеристического уравнения САР положительны, то для устойчивости системы необходимо и достаточно, чтобы среди определителей Гурвица 1, 2, …, n были положительными или все определители с четными индексами, или все определители с нечетными индексами.

10.3. Частотные критерии устойчивости

Описанные выше алгебраические критерии устойчивости не работают, если передаточная функция системы имеет запаздывание, т.е. может быть записана в виде

Wpc ( p) BA(( pp)) e p ,

где – запаздывание.

В этом случае характеристическое выражение замкнутой системы полиномом не является и его корни определить невозможно.

58

Для определения устойчивости в данном случае используются частотные критерии Михайлова и Найквиста.

10.3.1. Критерий Михайлова

Пусть характеристическое уравнение замкнутой системы имеет

вид

D( p) an pn an 1 pn 1 ... a2 p2 a1 p a0 0.

Произведем в данном характеристическом уравнении замену оператора Лапласа р на произведение j :

D( j ) an ( j )n an 1 ( j )n 1 ... a2 ( j )2 a1 ( j ) a0 0.

Функцию D( j ) Re[D( j )] j Im[D( j )] можно изобразить

на комплексной плоскости радиус-вектором, который называется годографом Михайлова.

Критерий Михайлова формулируется следующим образом: для устойчивой САР необходимо и достаточно, чтобы годограф Михайлова, начинаясь при нулевой частоте ( = 0) на положительной вещественной полуоси, обходил последовательно в положительном направлении (против часовой стрелки) при возрастании от 0 доn квадрантов, где n – степень характеристического полинома; если годограф Михайлова проходит через начало координат, то говорят, что система находится на границе устойчивости.

Иллюстрация к критерию Михайлова представлена на рис. 22.

а б в

Рис. 22. Устойчивость систем по критерию Михайлова: а – система устойчива; б – система на границе устойчивости; в – система неустойчива

59

Пример 9. Характеристический уравнение замкнутой системы имеет вид

D(р) = 2р4 + 5p3 + 10p2 + 6p + 1.

Определть устойчивость системы по критерию Михайлова.

Р е ш е н и е

Произведем замену р = j , в результате чего получим выражение для годографа Михайлова:

D(j ) = 2(j )4 + 5(j )3 + 10(j )2 + 6 j + 1 = = 2 4 – 5j 3 – 10 2 + 6 j + 1,

где Re( ) = 2 4 – 10 2 + 1 – действительная часть выражения годографа, Im( ) = –5 3 + 6 – мнимая часть.

Далее, варьируя частоту от 0 до бесконечности, на комплексной плоскости строим годограф Михайлова (рис. 23).

Рис. 23. Годограф Михайлова

Годограф Михайлова начинается на положительной действительной полуоси и последовательно обходит четыре квадранта (степень характеристического полинома n = 4), следовательно, система устойчива.

60