Анализ и синтез одноконтурных систем автоматического регулирования т

Регулятор – это управляющее устройство, осуществляющее автоматическое управление посредством аппаратной реализации алгоритмов управления.

Исполнительное устройство (ИУ) – это элемент системы управления, преобразующий сигнал команды управления, имеющий дискретную или аналоговую форму, в управляющее физическое воздействие непосредственно на объект управления.

Исполнительный механизм (ИМ) – это техническое устройство, предназначенное для преобразования входного сигнала – команды системы управления в изменение положения регулирующего органа, т.е. ИМ служит приводом регулирующего органа.

Регулирующий орган (РО) – это устройство, предназначенное для изменения (регулирования) расхода среды, энергии или какойлибо другой величины на объекте управления с целью обеспечения заданного режима его работы пропорционально изменению входного управляющего сигнала на ИУ.

Система автоматического регулирования (САР) – это сово-

купность объекта управления и управляющего устройства, которые без участия человека обеспечивают процесс регулирования.

Система автоматического управления (САУ) – это совокуп-

ность объекта управления и управляющего устройства, взаимодействие которых между собой обеспечивают процесс управления без участия человека.

Автоматизированная система управления (АСУ) – это челове-

ко-машинная система, обеспечивающая автоматизированный сбор и обработку информации, необходимой для оптимального управления в различных сферах человеческой деятельности.

2. Понятие передаточной функции

Как правило, системы автоматического управления технологических процессов при условии малости отклонения их входных и выходных величин от состояния равновесия могут с достаточной степенью достоверности рассматриваться как линейные системы.

11

В реальных АСУ ТП все технологические параметры изменяются во времени. Поэтому связь входных и выходных величин таких систем может описываться линейным дифференциальным уравнением вида

где x(t) и y(t) – входная и выходная величина системы соответственно; a0,…, an и b0,…, bm – постоянные коэффициенты.

В реальных (физически реализуемых) системах должно выполняться условие: n m .

Решение дифференциального уравнения будет являться функцией, описывающей динамику системы.

В случае, когда система имеет несколько входов и выходов, ее поведение может быть описано не одним, а большим числом уравнений.

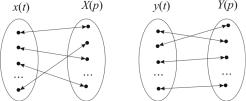
Для простоты решения линейных дифференциальных уравнений был разработан математический метод – преобразования Лапласа. В основе метода лежит идея, что каждому входному x(t) и выходному y(t) физическому сигналу (оригиналу) можно сопоставить некоторую другую функцию X(p) и Y(p) соответственно (изображение), получаемую по определенным правилам (рис. 3).

Рис. 3. Отображения физических сигналов

12

Последнее выражение является удобной формой записи дифференциального уравнения (1). Функция W(p) называется передаточной функцией.

Передаточная функция звена (линейной стационарной динамической системы) W(p) – это отношение изображения выходного сигнала L[y(t)] к изображению входного сигнала L[х(t)] при нулевых начальных условиях, т.е.

L y(t) W ( p) L x(t) .

Если уравнением (1) описывалась система, то полученная после вышеприведенных преобразований передаточная функция (2) будет являться передаточной функцией системы; если уравнение (1) описывало какой-то элемент системы (например, ОУ), то передаточная функция (2) будет являться передаточной функцией данного элемента (например, ОУ) системы.

Знаменатель передаточной функции называется характери-

стическим уравнением порядка n.

Пример 1, а. Объект управления описывается уравнением

7 p3Y ( p) 8 pY ( p) 3Y ( p) 4 p2 X ( p) 5X ( p) ,

или

Y ( p)[7 p3 8 p 3] X ( p)[4 p2 5] .

14

где b2 = 4, b1 = 0, b0 = 5, a3 = 7, a2 = 0, a1 = 8, a0 = 3.

Пример 1, б. Дано дифференциальное уравнение, характери-

Необходимо по заданному дифференциальным уравнениям определить операторные уравнения при нулевых начальных условиях, передаточные функции, структурные схемы звеньев, характеристические уравнения и их корни, показать распределение корней на комплексной плоскости иоценитьустойчивостькаждого иззвеньев.

Р е ш е н и е

Если обозначить Y(s), X(s) и U(s) как изображения сигналов y, x и u соответственно, то операторное уравнение (при нулевых начальных условиях) в данном случае примет вид

6,25s2Y(s) + 4sY(s) + Y(s) = 9X(s) – 1,2sX(s) – 5sU(s).

Данное уравнение можно преобразовать, вынеся Y(s) и X(s) за скобки:

Y(s)(6,25s2 + 4s + 1) = X(s)(9 – 1,2s) – 5sU(s).

Если обозначить передаточные функции объекта как

Wx (s) 9 21,2s 6,25s 4s 1

15

и

то получается уравнение Y(s) = Wx(s)X(s) + Wu(s)U(s). Ниже приведена структурная схема объекта.

Полученные передаточные функции имеют одинаковые знаменатели, называемые характеристическими выражениями

A(s) = 6,25s2 + 4s + 1.

Если приравнять данное выражение к нулю, то образуется характеристическое уравнение 6,25s2 + 4s + 1 = 0, корни которого

Распределение корней показывается на комплексной плоскости. По рисунку видно, что корни лежат в левой полуплоскости, следовательно, объект устойчив.

В случае, если необходимо получить из передаточной функции дифференциальное уравнение, все приведенные операции выполняются в обратном порядке.

Пример 2. Объект управления

имеет передаточную функцию

Получить дифференциальное уравнение, описывающее данный объект управления при нулевых начальных условиях.

16

Например, статическая характеристика регулятора (см. рис. 1) будет иметь вид

f ( ) ,

статическая характеристика объекта управления – y f ( ) .

3.2.Динамические (временные) характеристики

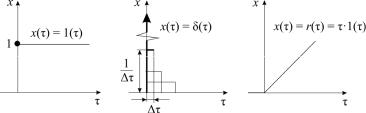
Одинамических свойствах системы судят по ее реакции на типовые входные воздействия (единичное ступенчатое, единичное импульсное, рамповое и т.д). Некоторые типовые входные воздействия представлены на рис. 4. Динамический (переходный) режим характеризуется переходом динамической системы из одного равновесного состояния в другое. Для переходного режима формулируются показатели качества управления, составляется математическое описание процессов, протекающих в объекте управления, ре-

шается задача синтеза структуры управляющего устройства с определением параметров настройки на основе заданных показателей качества управления, выполняется анализ и дается оценка работы системы в заданных условиях.

Рис. 4. Типовые входные воздействия: а – единичное ступенчатое воздействие; б – единичное импульсное воздействие; в – единичное рамповое воздействие

18

В прил. 2 приведены изображения типовых входных воздействий, а также некоторых других функций.

Таким образом, временной характеристикой звена называют закон изменения выходной величины звена во времени y(t) в ответ на изменение входного воздействия x(t) при условии, что до приложения входного воздействия звено находилось в покое.

Вместо термина «временная характеристика» часто применяют термин «кривая разгона», «переходная кривая» и др. Часто эту характеристику определяют не для единичного ступенчатого воздействия, а для ступенчатого воздействия произвольной величины. Временная характеристика имеет размерность, равную отношению размерностейвыходной ивходной величин системы иобозначается h(t).

Возможность описания свойств системы с помощью динамических характеристик (в частности, с помощью временных характеристик) базируется на применимости к таким системам принципа наложения, сущность которого может быть сформулирована следующим образом: реакция линейной системы на сумму входных воздействий равна сумме реакций на каждое из этих воздействий, взятых в отдельности.

Покажем, каким образом может быть определена реакция y(t) линейной системы на произвольное входное воздействие x(t), возникающее в момент времени t = 0, принятый за начало отсчета времени, если известна временная характеристика h(t) этой системы (предполагается, что до момента возникновения возмущения система находится в покое).

Любое физически реализуемое входное воздействие, возникающее в момент времени t = 0, может быть приближенно заменено «лестничной» функцией (рис. 5), которая, в свою очередь, может быть представлена суммой ступенчатых функций величиной х0 , х1, х2 ,.. , сдвинутых друг от друга на время t . Очевидно, вы-

брав величину t достаточно малой, можно достичь как угодно близкого совпадения «лестничной» и действительной функций.

19

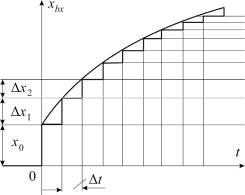
Рис. 5. Приближенная замена входного воздействиясуммойступенчатыхвоздействий

Каждое из полученных таким образом элементарных ступенчатых воздействии хk вызовет изменение выходной величины системы, которое будет отличаться от временной характеристики системы только постоянным множителем хk и, кроме того, будет сдвинуто относительно начала координат на время k t:

yk хk h(t k t) .

Приближенное значение выходной величины системы y в некоторый произвольный момент времени t n t будет равно сумме значений всех временных характеристик в этот момент:

n

y( ) х0h( ) xk h( k t) .

k 1

Поскольку результат, полученный с помощью этой формулы, будет тем точнее, чем меньшей выбрана величина t, то, переписав

ее в виде

20