
Численный расчет стержневых систем
..pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермский национальный исследовательский политехнический университет»
А.А. Суходоева
ЧИСЛЕННЫЙ РАСЧЕТ СТЕРЖНЕВЫХ СИСТЕМ
Утверждено Редакционно-издательским советом университета
в качестве учебного пособия
Издательство Пермского национального исследовательского
политехнического университета
2013
УДК 519.6 С91
Рецензенты:
канд. физ.-мат. наук, доцент Р.Г. Куликов (Пермский национальный исследовательский политехнический университет);
канд. физ.-мат. наук, научный сотрудник Е.А. Николаева (Институт механики сплошных сред УрО РАН, г. Пермь)
Суходоева, А.А.
С91 Численный расчет стержневых систем : учеб. пособие / А.А. Суходоева. – Пермь : Изд-во Перм. нац. исслед. поли-
техн. ун-та, 2013. – 70 с.
ISBN 978-5-398-01054-1
Изложен метод конечных элементов в перемещениях применительно к расчету стержневых систем. Подробно рассмотрены основные процедуры метода: построение матрицы жесткости и вектора сил отдельного элемента (ферменного, балочного), формирование глобальных матриц всей стержневой системы, определение узловых неизвестных и распределение внутренних усилий в стержнях.
Предназначено для студентов, обучающихся по направлению «Прикладная механика», при изучении численных методов в курсе «Строительная механика».
УДК 519.6
ISBN 978-5-398-01054-1 |
© ПНИПУ, 2013 |
2
|
ОГЛАВЛЕНИЕ |
|
Введение............................................................................................. |
4 |
|
1. |
Построение матрицы жесткости элемента................................... |
5 |
|
1.1. Понятие о матрице жесткости............................................... |
5 |
|
1.2. Преобразование координат.................................................... |
11 |
|
1.3. Ферменный элемент............................................................... |
16 |
|
1.4. Балочный элемент................................................................... |
20 |
2. |
Учет внеузловой нагрузки............................................................. |
37 |
3. |
Стержневая система....................................................................... |
41 |
|
3.1. Формирование матрицы жесткости и матрицы внешних |
|
|
сил стержневой системы............................................................... |
41 |
|
3.2. Определение узловых перемещений..................................... |
48 |
4. |
Примеры расчета............................................................................ |
53 |
|
4.1. Расчет плоской фермы ........................................................... |
53 |
|
4.2. Расчет многоопорной балки................................................... |
57 |
|
4.3. Расчет плоской рамы.............................................................. |
62 |
Список рекомендуемой литературы................................................. |
69 |
|
3
ВВЕДЕНИЕ
Стержневые системы широко применяются в различных областях промышленности: в строительстве, в авиа-, судо-, автомобиле- и приборостроении. В строительстве стержневые системы используются в многопролетных балках, ступенчатых валах, ферменных конструкциях, плоских и пространственных рамах, т.е. в элементах, испытывающих различные виды деформаций. Огромное количество однотипных стержней, входящих в стержневую систему, делает необходимым автоматизацию процесса их вычислений на прочность, жесткость и устойчивость. Эффективным средством расчета по-прежнему является метод конечных элементов.
В данном учебном пособии рассмотрен метод конечных элементов в перемещениях, где одному элементу соответствует один стержень, а узлу – места соединений стержней. Жесткостные характеристики стержней вычисляются здесь на основе соотношений технической теории бруса, известных из сопротивления материалов, и в рамках этой теории решение получается точным.
Материал изложен таким образом, что данный метод расчета может быть применен как для простого вида нагружения (одноосное растяжение-сжатие), так и для сложного пространственного напряженного состояния.
4
1. ПОСТРОЕНИЕ МАТРИЦЫ ЖЕСТКОСТИ ЭЛЕМЕНТА
1.1. Понятие о матрице жесткости
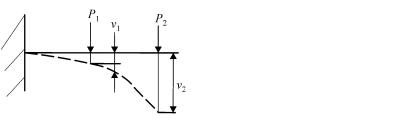
Рассмотрим консольную балку длиной l, нагруженную сосредоточенной силой на свободном конце (рис. 1.1). Как известно, вертикальное перемещение точки приложения силы
v = Pl3 /(3EJ ),
где E – модуль упругости; J – момент инерции поперечного сечения балки.
Если перемещение v задано, то из этой формулы можно найти силу, необходимую для создания такого перемещения: P =3EJv / l3 или P = kv, где k =3EJ / l3.
Величина k называется коэффициентом жесткости консольной балки. Если положить v =1, то сила P будет равна k. Отсюда вытекает физический смысл коэффициента жесткости: k есть сила, которую необходимо приложить на конце балки, чтобы его прогиб равнялся единице.
Рис. 1.1 |
Рис. 1.2 |
Пусть к балке приложены две силы, как показано на рис. 1.2. Используя известные методы сопротивления материалов, можно найти перемещения v1 и v2 в направлении действия этих сил:
v1 = δ11P1 ; v2 = δ21P2 ,
5
где δij (i, j = 1,2) – перемещение в направлении vi под действием единичной силы Pj . Величины δij , называемые коэффициентами
влияния, зависят от геометрических параметров балки и от модуля упругости материала.
Запишем связь между перемещениями и силами в матричной
форме: |
|
|
|
|
v = ∆P. |
|
(1.1) |
||
Здесь введены матрицы-столбцы сил и перемещений: |
||||
P |
|
v |
|
|
P = 1 |
|
; v = 1 |
|
, |
P2 |
v2 |
|
|
|
атакже матрица податливости
∆= δδ11 δδ12 .
21 22
Если принять, что перемещения v известны, то из (1.1) можно
найти силы Р, вызывающие эти перемещения: |
P = ∆−1ν. Полагая |
k = ∆−1 , придадим последнему равенству вид |
P = kν. Введенная |
здесь матрица k имеет размер 2×2 и называется матрицей жесткости рассматриваемой системы. Согласно теореме Максвелла о взаимности перемещений, справедливо равенство δ12 = δ21, т.е. матрица податливости ∆ является симметричной.
Теперь рассмотрим общий случай, когда на произвольное упругое тело действует система m сил (рис. 1.3), которую представим матрицей
P ={P1 P2 …Pm}т .
Пусть перемещения точек приложения сил Pi (в дальнейшем эти точки будем называть узлами) в направлении этих сил образуют матрицу
v ={v1 v2 …vm}т .
6
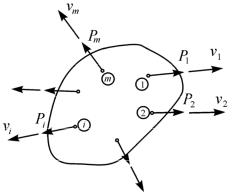
Здесь принято, что все перемещения vi отличны от нуля. Если
в некоторых из рассмотренных точек тело закреплено, то соответствующие элементы матрицы v будут равны нулю.
Рис. 1.3
Предположим, что перемещения заданы; тогда силы, необходимые для создания этих перемещений, определятся для линейноупругого тела соотношением
P = kv. |
(1.2) |
Матрица k, связывающая силы P |
с соответствующими им |
перемещениями v, называется матрицей жесткости рассматриваемого тела.
Представим соотношение (1.2) в развернутом виде:
P1
P2...
=Pi
...Pm
k11
k21
...
ki1
...
km1
k12 |
... |
k1 j |
k22 |
... |
k2 j |
... ... ... |
||
ki2 |
... |
kij |
... ... ... |
||
km2 |
... |
kmj |
7
... |
k1m v1 |
|
|
|||
... |
k |
|
v |
|
|
|
|
|
2m |
2 |
|
|
|
... |
... |
|
... |
(1.3) |
||
... |
|
|
|
|
|
|
kim vj |
|
|
||||
... |
... |
|
... |
|
||
... |
|
|
|
|
|
|
kmm vm |
|
|||||
|
|
|
|
|
|
|
Выпишем i-ю строку этого матричного равенства:
Pi = ki1v1 +ki2v2 +…+kijvj +…+kimvm .
Физический смысл коэффициента kij можно выяснить, полагая перемещение vj равным 1, а все остальные перемещения равными нулю; тогда Pi = kij . Отсюда следует, что коэффициент жесткости kij представляет собой силу, возникающую в узле i, когда перемещение vj равно единице, а все остальные перемещения равны нулю. Иначе говоря, если закрепить тело во всех узлах, кроме узла j, и приложить такую силу Pj , чтобы перемещение vj равнялось единице, то реакция на тело в узле i будет равна kij (при этом величина самой силы Pj определит значение коэффициента k jj ).
Применяя теорему Бетти о взаимности работ, можно показать, что матрица жесткости всегда симметрична.
Если силы Pi имеют произвольные направления, то удобно разложить эти силы по координатным осям x, y, z и ввести для ка-
ждого узла i матрицу сил Pi ={Pix Piy Piz }т . Тогда vi будет также матрицей-столбцом, элементы которой суть перемещения узла i по координатным осям: vi ={vix viy viz }т . Связь между силами и пере-
мещениями можно по-прежнему определить соотношением вида (1.3), только элементами kij матрицы k, представляющей уже
блочную матрицу, будут квадратные подматрицы размером 3×3. Для практических вычислений удобнее иногда пользоваться
сквозной нумерацией компонент узловых сил и перемещений. В этом случае силы P1x , P1y , P1z , действующие в узле l, обозначают-
ся соответственно P1, P2 , P3; силы P2 x , P2 y , P2z , действующие в уз-
8
ле 2, – P4 , P5 , P6 и т.д. При такой индексации элементы матрицы сил для узла i будут иметь номера 3i −2, 3i −1, 3i, т.е.
|
|
Pix |
|
|
P3i−2 |
|
||
P |
= |
P |
|
= |
P |
−1 |
. |
|
i |
|
iy |
|
|
|
3i |
|
|
|
|
|
|
|
P |
|
|
|
|
|
Piz |
|
|
|
3i |
|
|
Аналогично для перемещений имеем:
|
|
|
vix |
|
|
v3i−2 |
|
||
v |
i |
= |
v |
|
= |
v |
−1 |
. |
|
|
|
iy |
|
|
|
3i |
|
||
|
|
|
|
|
|
v |
|
|
|
|
|
|
viz |
|
|
|
3i |
|
|
Наконец, в самом общем случае в каждом узле могут помимо сил действовать моменты относительно координатных осей. Тогда подматрицы Pi и vi будут состоять из шести компонент, которые мы условимся перечислять в следующем порядке:
Pi ={Pix Piy Piz Mix Miy Miz }т ;
vi ={vix viy viz θix θiy θiz }т ,
(1.4)
где Mig и θig – момент и угол поворота относительно оси g
(g = x, y, z).
Если использовать сквозную нумерацию сил и перемещений, то вместо (1.4) следует писать:
Pi ={P6i−5 P6i−4 P6i−3 P6i−2 P6i−1 P6i}т ; vi ={v6i−5 v6i−4 v6i−3 v6i−2 v6i−1 v6i}т .
Положительные направления сил и моментов показаны на рис. 1.4, а, линейных и угловых перемещений – на рис. 1.4, б; моменты и угловые перемещения представляются векторами в соответствии с правилом правого винта.
9

а |
б |
|
Рис. 1.4 |
Подматрица ki j |
будет иметь размер 6×6. Смысл отдельных |
элементов этой подматрицы можно выяснить, полагая, как и ранее, все перемещения (линейные и угловые) равными нулю, за исключением одного, которое берется равным единице. Так, коэффициент
k6i−2, 6i−3 |
равен обобщенной силе P6i−2 (т.е. Mix ), которая возникает |
в узле i, |
если v6i−2 (т.е. vjz ) равно 1, а остальные пять перемещений |
узла j и все перемещения остальных узлов равны нулю.
Вычисление матриц жесткости отдельных конструктивных элементов, из которых состоит стрежневая система, составляет важный этап ее расчета матричным методом перемещений. Узлами для элементов служат точки соединения их друг с другом. Для расчета матриц жесткости элементов могут применяться различные способы. Мы остановимся на трех из них как наиболее простых
иупотребительных.
Впростейших случаях можно исходить непосредственно из физического смысла коэффициентов жесткости; этот подход иллюстрируется ниже (см. подразд. 1.3) на примере прямолинейного стержня, работающего на растяжение-сжатие (ферменного элемента).
10
