
Численный расчет стержневых систем
..pdf3.СТЕРЖНЕВАЯ СИСТЕМА
3.1.Формирование матрицы жесткости
иматрицы внешних сил стержневой системы
Рассмотрим стержневую систему, отнесенную к некоторой системе координат x, y, z. Пусть vi – матрица перемещений типово-
го узла i. Число элементов этой матрицы (число степеней свободы узла) зависит от типа конструкции. Так, для пространственной фермы матрица vi будет содержать три перемещения узла в направлении координатных осей:
vi ={vix viy viz }т ,
а для плоской фермы – два перемещения:
vi ={vix viy }т .
В случае пространственной рамы матрица vi =
={vix viy vizθix θiy θiz }т состоит из трех линейных смещений и трех углов поворота. Если же плоская рама нагружена силами в своей плоскости, то матрица vi ={vixviyθi}т включает в себя два линейных
смещения и угол поворота.
Матрицу внешних сил, действующих в узле i в направлении
перемещений |
vi , обозначим Pi . Число элементов этой матрицы |
|
совпадает |
с |
числом степеней свободы узла; перечислять силы |
в матрице |
Pi |
всегда будем в том же порядке, в каком перемещения |
располагаются в матрице vi. Например, для пространственной рамы
Pi ={Pix Piy Piz Mix Miy Miz }т .
41
Матрицы узловых сил и перемещений для всей конструкции обозначим буквами P и v и составим их следующим образом:
|
P1 |
|
|
|
v1 |
|
|
||
|
P |
|
|
|
v |
|
|
||
P = |
|
2 |
|
; |
v = |
|
2 |
|
, |
|
|
|
|
|
|
||||
|
... |
|
|
|
... |
|
|
||
|
|
|
|
|
|
|
|
||
|
P |
|
|
|
v |
|
|
||
|
|
m |
|
|
|
m |
|
||
где m – число узлов стержневой системы.
При отсутствии внеузловой нагрузки связь между матрицами Р и v может быть представлена в виде P = kv, где k – матрица жест-
кости системы.
Если же помимо узловых сил действуют внеузловые нагрузки, то можно рассуждать так же, как и в случае отдельного стержня. Предположим, что все узлы защемлены; тогда в результате действия внеузловой нагрузки со стороны наложенных связей возникнут силы реакции. Перечисляя реакции, действующие в узле i, в том
же порядке, что и для матрицы Pi , образуем матрицу P0i ; число
элементов этой матрицы совпадает, конечно, с числом степеней свободы узла. Для всей конструкции можно составить матрицу
|
P01 |
|
|
P |
|
P = 02 |
. |
|
0 |
... |
|
|
|
|
|
|
|
|
P |
|
|
0m |
|
Если, далее, узлы имеют некоторые смещения v, то для их создания необходимо дополнительно приложить силы, величина которых зависит от жесткостных характеристик системы; матрица этих сил может быть вычислена как произведение kv. Таким образом, связь между узловыми силами и узловыми перемещениями можно в общем случае записать так:
P = kv + P0. |
(3.1) |
42
Покажем теперь, как можно найти матрицы k и P0 , зная матрицы k(e) и P0(e) для отдельных конструктивных элементов, обра-
зующих систему. Запишем прежде всего уравнение (3.1) в блочной форме:
P |
|
|
k11 ...k1 j ...k1m |
|
v |
|
|
|
P |
|
|
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
01 |
|
|
|
... |
|
|
........................ |
... |
|
|
... |
|
|
||||||||||
P |
|
= k |
|
...k |
|
...k |
|
|
|
v |
|
|
+ |
P |
. |
|
|||
i |
|
|
|
|
i1 |
|
|
ij |
|
im |
|
|
|
j |
|
|
0i |
|
|
... |
|
|
........................ |
... |
|
|
... |
|
|
||||||||||
|
|
|
|
k |
|
|
...k |
...k |
|
|
|
|
|
|
|
|
|
||
Pm |
|
|
|
|
|
|
v |
|
|
|
P0m |
|
|||||||
|
|
|
|
m1 |
|
|
|
|
|
|
m |
|
|
|
|
||||
|
|
|
|
|
|
mj mm |
|
|
|
|
|||||||||
Выпишем его i-ю строку: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Pi |
= ki1v1 + ... + kijv j |
+ ... kimvm |
+ P0i . |
(3.2) |
|||||||||||||||
Для вычисления |
подматриц |
|
ki1 , ..., kim , |
а |
также |
подматри- |
|||||||||||||
цы P0i рассмотрим равновесие узла i. В качестве примера на рис. 3.1
показан узел плоской рамы со всеми сходящимися в нем стержнями. Выделим один из конструктивных элементов, соединяющихся в узле i (например, стержень 1). Рассматриваемый элемент соединяет узел i с некоторым другим узлом g. Пусть матрица жесткости
этого типового элемента в общей системе координат равна k(e). Силы P(e) = {Pi(e) Pg(e)}, действующие в узлах данного стержня, свя-
заны с перемещениями |
v(e) = {vi |
vg } его узлов соотношением |
P(e) = k(e)v(e) + P0(e) , где |
P0(e) = {P0(ie) |
P0(ge)} – матрица реакций, воз- |
никающих в узлах элемента от внеузловой нагрузки при v(e) = 0. Перепишем это соотношение в блочной форме:
P(e) |
k(e) |
k(e) |
|
v |
i |
|
P(e) |
||||||
|
i |
|
= |
i i |
i g |
|
|
+ |
0i |
. |
|||
|
|
|
|
vg |
|
|
|||||||
P(e) |
k(e) |
k(e) |
|
|
P(e) |
||||||||
|
g |
|
|
g i |
gg |
|
|
|
|
0 g |
|
||
|
|
|
|
|
43 |
|
|
|
|
|
|
|
|
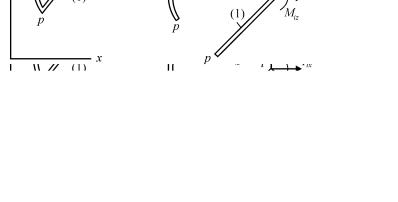
Рис. 3.1
Отсюда получим выражение для матрицы сил, действующих в узле i на рассматриваемый элемент:
P |
(e) = k(e)v |
i |
+ k(e)v |
g |
+ P(e). |
(3.3) |
i |
ii |
ig |
0i |
|
Соединим теперь все стержни; тогда из условия равновесия уз-
ла имеем Pi = ∑ Pi(e) , где суммирование ведется по всем стержням,
сходящимся в узле i. Подставляя сюда выражение (3.3), получаем:
P |
= ∑ k(e) v |
+ ∑ k(e) v |
g |
+ ∑ P(e). |
(3.4) |
i |
ii i |
ig |
0i |
|
Для представленного на рис. 3.1 примера равенство (3.4) примет вид (верхний индекс в скобках означает номер стержня)
Pi = (kii(1) + kii(2) + kii(3) + kii(4) )vi + (kip(1) + kip(2) )vp +
+ k(3)v |
g |
+ k(4)v + P(1) + P(2) + P(3) + P(4). |
(3.5) |
||||
ig |
is s |
0i |
0i |
0i |
0i |
|
|
Сопоставим полученный результат с равенством (3.2). Прежде всего замечаем, что в формуле (3.5) (или для общего случая в (3.4)) отсутствуют члены, содержащие перемещения тех узлов j, которые
44
не связаны стержнем непосредственно с узлом i. Это означает, что соответствующие подматрицы ki j являются нулевыми. Если узел j
связан с узлом i одним стержнем (в рассматриваемом примере таковыми являются узлы g и s), то множителем при vj оказывается
подматрица ki(ej ) этого элемента, поэтому для таких узлов kij = kij(e). Если же узел j связан с узлом i несколькими элементами (узел p на рис. 3.1), то множителем при vj будет сумма подматриц kij(e) эле-
ментов, соединяющих узлы i и j, т.е. в этом случае ki j = ∑ k ie j . Наконец, множитель при vi , являющийся диагональной подматрицей матрицы k, kii = ∑ kii(e) , где суммирование выполняется по всем эле-
ментам, сходящимся в узле i.
Из сказанного следует, что матрицу жесткости стержневой системы можно образовать из матриц жесткости разрозненных конструктивных элементов по следующему правилу: ki j = 0, если узлы
i и j не связаны непосредственно никаким элементом; ki j = ∑ kij(e) , если узлы i и j связаны несколькими элементами (суммирование
выполняется по этим элементам), сходящимися в узле i. Все эти случаи можно объединить общей формулой
kij = ∑ kije (i, j = 1, 2, ..., m) , |
(3.6) |
где суммирование выполняется по всем конструктивным элементам, входящим в стержневую систему. При этом следует принимать
для элемента kij(e) = 0, если этот элемент не соединяет узлы i, j.
Таким образом, для получения матрицы жесткости стержневой системы можно все элементы матрицы жесткости каждого стержня
k(e) |
k(e) |
k(e) = i i |
i j |
k(e) |
k(e) |
j i |
j j |
45
поместить в соответствующие ячейки общей матрицы жесткости (положение ячеек определяется нижними индексами) и произвести затем суммирование всех накладывающихся элементов.
Аналогичное правило суммирования применяется и для вычисления матрицы P0. Сравнивая последние слагаемые в (3.2) и (3.4), заключаем, что подматрицу P0i можно найти по формуле
P |
= ∑ P(e) , |
(3.7) |
0i |
0i |
|
где суммирование ведется по всем конструктивным элементам, сходящимся в узле i.
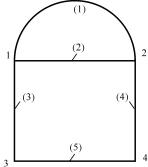
Поясним схему формирования общей матрицы жесткости на примере плоской рамы (рис. 3.2).
Эта рама имеет четыре узла и включает в себя пять стержней. Матрицы жесткости стержней в общей системе координат представим в блочной форме:
k(1) |
k(1) |
|
k(2) |
k(2) |
|
k(1) = 11 |
12 |
; |
k(2) = 11 |
12 |
; |
k(1) |
k(1) |
|
k(2) |
k(2) |
|
21 |
22 |
|
21 |
22 |
|
k(3) |
k(3) |
; |
k(4) |
k(4) |
; |
||
k(3) = |
11 |
13 |
k(4) = |
2 2 |
24 |
||
|
(3) |
(3) |
|
|
(4) |
(4) |
|
k31 |
k33 |
|
k42 |
k44 |
|
||
k(5) |
k(5) |
|
|
|
|
|
|
k(5) = |
33 |
34 . |
|
|
|
|
|
k(5) |
k(5) |
|
|
|
|
|
|
|
43 |
44 |
|
|
|
|
|
Напомним, что нижние индексы i, j означают номера узлов данного стержня, а верхний индекс – номер стержня.
В соответствии с числом узлов рамы матрица жесткости системы k будет иметь 4×4 блока. Подматрицы ki j (i, j =1, 2, 3, 4) об-
разуются путем суммирования всех подматриц жесткости отдельных элементов с одинаковыми нижними индексами. Так, подматри-
ца k12 = k12(1) + k12(2). В итоге получим:
46
k |
(1) |
+ k |
(2) |
+ k(3) |
| k |
(1) |
+ k |
(2) |
|
|
| k(3) |
|
|
| 0 |
|
|
1 |
||
|
11 |
11 |
11 |
12 |
12 |
|
(4) |
13 |
|
|
|
(4) |
|
|
|
||||
|
k |
(1) |
+ k |
(2) |
|
| k |
(1) |
+ k |
(2) |
+ k |
| 0 |
|
|
| k |
|
|
2 |
||
|
21 |
21 |
|
22 |
22 |
22 |
|
|
24 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
k |
(3) |
|
|
|
| 0 |
|
|
|
|
| k(3) |
+ k |
(5) |
| k |
(5) |
|
|
3 |
||
|
|
31 |
|
|
|
|
|
|
|
|
|
33 |
33 |
|
34 |
|
|
|
|
|
|
|
|
|
|
|
(4) |
|
|
|
|
(5) |
|
|
|
(4) |
(5) |
4 |
|
k = 0 |
|
|
|
| k42 |
|
|
|
|
| k43 |
|
|
| k44 |
+ k44 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
4 |
|
|
Некоторые подматрицы (например, k14 ) оказались нулевыми,
так как соответствующие узлы непосредственно не связаны между собой стержнем.
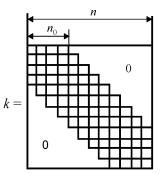
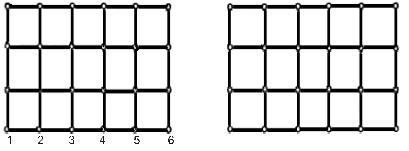
Расположение нулевых подматриц в матрице жесткости k определяется порядком нумерации узлов. Нумеруя узлы определенным образом, можно иногда добиться того, чтобы все ненулевые подматрицы были сгруппированы вблизи главной диагонали, т.е. добиться ленточной структуры матрицы жесткости (рис. 3.3). Примеры такой нумерации узлов показаны на рис. 3.4 для случая плоской рамы. Рассмотрим, например, узел 10 в схеме 3.4, а. Максимальный номер узла, с которым он связан непосредственно стержнем, 16, минимальный – 4. Поэтому в десятой стро-
ке матрицы жесткости k (записанной в блочной форме) первая ненулевая подматрица появится в четвертом, а последняя – в шестнадцатом столбце. Выпол-
няя подобные рассуждения для других Рис. 3.3 узлов, можно убедиться, что все ненуле-
вые подматрицы образуют ленту коэффициентов, ширина которой
вданном примере постоянна и равна 13 подматрицам. Учитывая симметрию матрицы жесткости, можно говорить о полуленте, ширина которой (включая диагональную подматрицу) равна 7. Поскольку
вслучае плоской рамы каждая подматрица имеет размер 3×3, фактическая ширина полуленты будет равна 21.
47
19 |
20 |
21 |
22 |
23 |
24 |
4 |
8 |
12 |
16 |
|
20 |
24 |
13 |
14 |
15 |
16 |
17 |
18 |
3 |
7 |
11 |
15 |
|
19 |
23 |
7 |
8 |
9 |
10 |
11 |
12 |
2 |
6 |
10 |
14 |
|
18 |
22 |
|
|
|
|
|
|
1 |
5 |
9 |
|
13 |
17 |
21 |
|
|
а |
|
|
|
|
|
|
б |
|
|
|
Рис. 3.4
Ленточная структура матрицы жесткости обладает большими вычислительными достоинствами по сравнению со случаем полного заполнения. Во-первых, в памяти ЭВМ нет надобности хранить всю подматрицу: достаточно иметь лишь те коэффициенты, которые заключены внутри полуленты. Поскольку ее ширина n0 часто значи-
тельно меньше размера матрицы n, то это позволяет достичь существенной экономии памяти, что весьма важно в задачах с большим числом степеней свободы. Во-вторых, все операции, в которых участвует матрица жесткости, можно выполнять только с теми элементами, которые ограничены шириной ленты; это значительно экономит время вычислений. Чем меньше ширина ленты, тем эффективнее будет решение задач. Поэтому всегда следует тщательно продумывать порядок нумерации узлов. Так, в рассмотренном выше примере более удачной является схема нумерации узлов, показанная на рис. 3,4, б. Она приводит к ленточной матрице с шириной полуленты, равной 15.
3.2. Определение узловых перемещений
До сих пор мы полагали, что зависимость (3.1) служит для определения сил P, необходимых для создания известных перемещений v. Если же, наоборот, известны силы, действующие в узлах
48
конструкции, то (3.1) можно рассматривать как систему алгебраических уравнений относительно перемещений v.
Если конструкция закреплена, то перемещения соответствующих узлов в направлении опорных связей равны нулю, остальные же перемещения подлежат отысканию. Все компоненты перемещений можно расположить таким образом, чтобы в матрице v сначала перечислялись все неизвестные, а затем – известные (нулевые) перемещения. Тогда матрица v будет представлена в блочной форме
v= vvα ,
β
где подматрица vα содержит только неизвестные перемещения, а подматрица vβ нулевая. Порядок перечисления сил в матрицах Р
и Р0 всегда должен строго соответствовать порядку следования перемещений в матрице v:
P |
|
|
P |
α |
|
||
P = |
α |
|
; |
P0 = |
0 |
. |
|
|
P |
|
|
|
P |
β |
|
|
|
0 |
|||||
β |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
В подматрицу Pα входят известные силы, действующие в направлении перемещений vα. Подматрица Pβ содержит силы, дейст-
вующие по направлению наложенных связей и представляющие собой реакции опор.
Строки и столбцы матрицы жесткости k мы должны расположить в том же порядке, в котором силы и перемещения перечисляются в матрицах P и v, т.е. матрица жесткости будет иметь следующую блочную структуру:
kαα |
kαβ |
|
k = |
kββ |
. |
kβα |
|
|
|
|
|
49
Представляя уравнение (3.1) в развернутом виде и учитывая, что vβ = 0, получим:
kαα |
kαβ |
vα |
Pα |
|
P0α |
||||
k |
k |
|
0 |
|
= P |
|
− P |
. |
|
βα |
|
ββ |
|
|
|
|
|
0 |
β |
|
|
|
|
|
β |
|
|
||
|
|
|
|
|
|
|
|
|
|
Отсюда следует два матричных равенства |
|
||||||||
|
kααvα = Pα − P0α; |
|
(3.8) |
||||||
|
|
kβαvα = Pβ − P0β. |
(3.9) |
||||||
Решая уравнение (3.8), находим неизвестные перемещения vα, а уравнение (3.9) позволяет найти реакции опор:
Pβ = kβαvα + P0β.
Заметим, что практически нет необходимости производить перестановку элементов матриц P, P0 , k. Матрицы Pα и P0α можно
получить, вычеркнув в исходных матрицах P и P0 элементы, соответствующие опорным связям; при этом вычеркнутые члены составят матрицы Pβ и P0β. Матрица kαα получится также вычеркива-
нием соответствующих строк и столбцов из полной матрицы k. Матрица kββ будет образована элементами, находящимися на пере-
сечении вычеркнутых строк и столбцов, а матрица kβα – элемента-
ми на пересечении вычеркнутых строк и оставшихся столбцов. Пользуясь аналогичными рассуждениями, можно рассмотреть
и более общий случай, когда заданные перемещенияvβ не равны нулю. Тогда вместо (3.8) и (3.9) имеем:
kααvα = Pα − P0α −kαβvβ;
Pβ = kβαvα + kββvβ + P0β.
50
