
Математика. Функции одной переменной. Пределы. Дифференцирование (110
.pdfCopyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
11
1.4. Сравнение бесконечно малых величин |
|
|
|||||||||||
1º. Бесконечно малые. |
|
|
|
|
|
||||||||
Если |
lim (x) 0, т.е. если |
|
|
|
|||||||||
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
(x) |
|
|
при |
0 |
|
x a |
|
( ) , то |
функция |
(x) |
называется |
|
|
|
|
|
||||||||||
бесконечно малой при x a . |
|
|
|
||||||||||
Пусть |
(x) |
и |
(x) |
|
бесконечно малые |
при |
x a . Если |
||||||
lim (x) |
1, |
|
|
|
|
|
|
|
( 12 ) |
||||
x a (x) |
|
|
|
|
|
|
|
|
|
|
|||
то бесконечно |
малые |
называются |
эквивалентными. Пишут: |
||||||||||
(x) ~ (x).
Теорема 1.3. Если отношение двух бесконечно малых имеет предел, то этот предел не изменится при замене каждой из бесконечно малых
эквивалентной ей бесконечно малой, то есть если lim m, ~ |
, ~ |
1 |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
1 |
lim |
m . |
|
|
|
|
|
( 13 ) |
|
|
|
||||||
x a |
|
|
1 |
x a |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полезно использовать эквивалентность следующих бесконечно малых: |
||||||||||||||||||
если 0 , то |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
sin ~ , |
tg ~ , |
arcsin ~ , arctg ~ ; |
|
|
|
|
||||||||||||
ln 1 ~ , |
|
|
|
|
1 m 1 ~ m ; |
( 14 ) |
|
|
|
|||||||||
a 1 ~ ln a, |
|
|
|
|
||||||||||||||
а также значения некоторых пределов: |
|
|
|
|
||||||||||||||
lim |
ln(1 ) |
1 , |
|
|
|
|
|
( 15 ) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
a 1 |
ln a , |
|
|
|
|
|
( 16 ) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
lim 1 m 1 m . |
|
|
|
|
|
( 17 ) |
|
|
|
|||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Здесь (x) - бесконечно малая функция. |
|
|
|
|
||||||||||||||
Пример 15. |
Найти |
lim |
|
sin x 3 |
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
x 3 x2 4x 3 |
|
|
|
|
||||
Решение. |
|
При x 3, |
x 3 0 , следовательно, |
sin(x 3) ~ x 3 |
||||||||||||||
(см. (14)) . Используя (13) и теорему об эквивалентности бесконечно малых, имеем
lim |
sin x 3 |
|
lim |
|
x 3 |
|
lim |
1 |
|
1 |
. |
|
x2 4x 3 |
x 3 x 1 |
|
|
|||||||||
x 3 |
x 3 |
x 3 |
x 1 2 |
|||||||||
Пример 16. Найти |
lim |
cos4x cos2x |
. |
|
|
|
||||||
|
|
|
|
|||||||||
|
|
|
|
x 0 |
arcsin2 3x |
|
|
|
|
|||

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
12
Решение. По формуле тригонометрии
cos4x cos2x 2sin |
4x 2x |
sin |
|
4x 2x |
2sin 3x sin x. |
|
|
|
||||||
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
2 |
|
|
|
arcsin3x 2 |
~ 3x 2 . |
|||
При x 0 sin 3x ~ 3x, |
sin x ~ x, arcsin3x ~ 3x , то есть |
|||||||||||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
cos4x cos2x |
lim |
2sin 3x sin x |
lim |
2 3x x |
|
2 |
. |
|
|||||
arcsin2 3x |
arcsin2 |
|
|
3x 2 |
3 |
|
||||||||
x 0 |
x 0 |
3x |
x 0 |
|
|
|
||||||||
Контрольные примеры
|
|
|
|
|
|
|
|
|
lim |
sin x sin a |
||||
1. |
lim |
n 1 |
n |
2. |
||||||||||
|
x a |
|||||||||||||
|
n |
|
|
|
|
|
|
x a |
||||||
4. |
lim |
|
sin x cos x |
|
5. |
lim |
1 cos5x |
|
||||||
|
|
4x |
|
|
|
1 cos3x |
||||||||
|
|
|
|
|
|
|
|
x 0 |
||||||
|
x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3. lim cosmx cosnx
x 0 x2
6. lim tg x
x 2 x 2
|
|
|
|
|
|
|
|
|
|
|
7. lim |
sin 2x |
8. lim |
|
x 1 |
9. lim |
|
x 1 |
|||
|
x 1 |
|
|
|
|
|||||
x 0 ln(1 x) |
x 1 |
x 1 |
3 |
x 1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x x2 2 |
|||||||||||
|
|
|
|
|
2x 3 |
|
|
|
|
x2 23 x 1 |
|
|
|
||||||||||||||||||||||||||||
10. |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
11. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12. |
lim |
|
|
|
|
|
|
|
|||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
x 1 2 |
|
|
x 1 |
||||||||||||||||||||||
|
x x |
|
|
x |
|
|
|
|
x 1 |
|
|
|
|
x 1 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 8 x |
||||||||||||
|
|
|
|
|
|
|
x2 2x 6 x2 2x 6 |
|
|
||||||||||||||||||||||||||||||||
13. |
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14. |
lim |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
x2 4x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x |
2 |
||||||||||||||
|
|
|
|
|
x |
|
|
|
x |
|
|
|
|
|
|
sin 3x sin 5x |
|
|
|
ln x |
|||||||||||||||||||||
15. |
lim |
|
|
|
|
|
|
|
|
|
|
|
16. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
17. lim |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
(x x3 )2 |
|
|
|
|
|
|
||||||||||||||||||||||||
|
x x |
1 |
|
|
|
|
x 0 |
|
|
|
x 1 |
1 |
x |
||||||||||||||||||||||||||||
|
|
|
arcsin |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
cos x cos2x |
|
|
|
ln(1 ax) |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
x2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
18. lim |
|
|
|
|
|
1 |
|
|
19. lim |
|
20. lim |
||||||||||||||||||||||||||||||
|
|
|
|
ln(1 x) |
|
|
|
|
|
1 cos x |
|
x |
|||||||||||||||||||||||||||||
|
x 0 |
|
|
|
|
|
x 0 |
|
|
|
|
x 0 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln(3x2 5x 21) |
||||||||||||||||||||||
|
5 |
1 x 1 |
|
|
|
|
|
3 |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
1 x |
|
|
|
||||||||||||||||||||||||||||||||
21. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22. lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
23. lim |
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x2 6x 8 |
|||||||||||||||||||
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
x 2 |
|
|||||||||||||||||||

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
2. Производная и дифференциал |
|
|
|
|
|
|||||||||||||
2.1. |
|
|
Определение производной |
|
|
|
|
|
||||||||||
Производной функции y f (x) |
в точке |
x |
называется конечный |
|||||||||||||||
предел |
при |
x 0 |
отношения приращения |
функции в этой точке к |
||||||||||||||
приращению аргумента (при условии, что этот предел существует). |
||||||||||||||||||
lim |
|
|
f x x f (x) |
lim |
f f / (x) . |
|
|
|
( 1 ) |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
x 0 |
|
|
x |
|
|
|
x 0 |
x |
|
|
|
|
|
|||||
Нахождение производной называется дифференцированием функции. |
||||||||||||||||||
Пример 1. |
Найти производную функции f (x) x2 . |
|
||||||||||||||||
Решение. |
|
Давая |
аргументу |
x |
приращение |
x . Найдем |
||||||||||||
соответствующее приращение функции |
|
|
|
|
|
|||||||||||||
f f (x x) f (x) (x x)2 x2 x2 2x x ( x)2 |
|
|||||||||||||||||
Составим отношение |
|
|
|
|
|
|
||||||||||||
f |
|
2x x ( x)2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
Найдем предел этого отношения при x 0 . |
|
|
||||||||||||||||
lim |
f |
lim |
2x x ( x)2 |
|
2x . |
|
|
|
|
|
||||||||
x |
|
|
x |
|
|
|
|
|
||||||||||
x 0 |
x 0 |
|
|
|
|
|
|
|
|
|||||||||
Следовательно, производная функции |
f (x) x2 |
равна 2x , что можно |
||||||||||||||||
записать так: (x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
) 2x. |
|
|
|
|
|
|
|
|
|
|||||||||
Геометрический смысл производной
Касательная в геометрии определяется как прямая, имеющая с окружностью одну общую точку. Такое определение касательной не может быть перенесено на все кривые. Если применить его к параболе 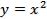 , то в начале координат обе координатные оси подошли бы под это определение.
, то в начале координат обе координатные оси подошли бы под это определение.
Для введения определения касательной к прямой рассмотрим функцию
и ее график. Путь точка |
— фиксированная |
|||
точка графика функции, соответствующая |
значению |
аргумента |
||
; точка |
— соответствует значению аргумента |
. |
||
Проведем через точки |
прямую и назовем ее секущей. |
|
|
|
Определение. Касательной к графику функции |
y f (x) |
в точке |
|
|
будем называть предельное положение секущей M0 M при стремлении точки |
||||
M графика функции к точке |
M0 или, что то же самое, при стремлении |
x к |
||
нулю (если оно существует). |
|
|
|
|
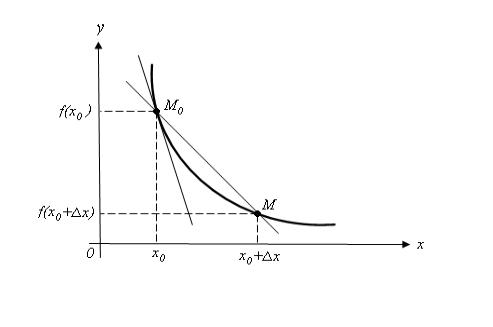
14
Уравнение секущей, проходящей через две точки, |
M и M0 имеет вид: |
|||||||||||||||||||||||||
y f (x ) |
f |
x0 x f (x0 ) |
(x x |
) |
. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
0 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Если |
функция |
y f (x) |
|
дифференцируема в |
|
точке |
(x x0 ) , |
то |
||||||||||||||||||
предельное положение секущей |
M0 M , |
|
при стремлении точки M к точке |
|||||||||||||||||||||||
M0 (при |
x 0 ) существует, |
и ее уравнение (уравнение касательной к |
||||||||||||||||||||||||
графику функции y f (x) в точке M0 |
следующее |
|
|
|
|
|
||||||||||||||||||||
y f (x0 )(x x0 ) f (x0 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
равна |
|
угловому коэффициенту касательной |
||||||||||||
Итак, производная f (x0 ) |
|
|
||||||||||||||||||||||||
к графику функции y f (x) в точке M0 |
, т.е. тангенсу ее угла наклона к оси |
|||||||||||||||||||||||||
Ox. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1º. Основные правила нахождения производной. |
|
|
|
|||||||||||||||||||||||
Пусть C const, u u(x), v v(x) |
- дифференцируемые функции. |
|
||||||||||||||||||||||||
Тогда: |
|
|
|
2) Cu / |
|
|
|
|
|
|
|
|
3) u v / |
|
|
|
||||||||||
1) C / 0; |
|
|
Cu / ; |
|
|
|
|
|
u / |
v/ ; |
|
|||||||||||||||
|
|
/ |
/ |
|
/ |
|
|
|
|
|
|
u |
/ |
|
|
u / v uv |
/ |
|
|
|
|
|||||
4) uv |
u |
v uv |
; |
|
|
|
5) |
|
|
|
|
|
|
|
|
|
; |
|
|
|
||||||
|
|
|
|
|
|
v2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|||
6) |
если |
|
y f (u), |
|
|
u u(x), |
имеют |
производные, |
то |
|||||||||||||||||
y / (x) y / (u) u / (x) |
(правило дифференцирования сложной функции). |
|||||||||||||||||||||||||
7) |
Пусть y f (x) |
и |
x ( y) - взаимно обратные функции, y f (x) |
|||||||||||||||||||||||
имеет |
производную |
( f |
|
|
|
|
тогда |
обратная |
функция имеет |
|||||||||||||||||
|
(x) 0), |
|
||||||||||||||||||||||||
производную xy |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
15
2º. Таблица производных основных функций
1. (xn ) nxn 1.
2. |
|
|
|
|
1 |
|
|
(x 0) . |
|
|
|
||||||
|
|
|
|
|
||||
( x ) |
2 x |
|
||||||
3.(sin x) cosx .
4.(cos) sin x .
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5. |
(tgx) |
cos2 x . |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
(ctgx) |
sin 2 x . |
|
|
|||||||||||||||
|
|
|
|||||||||||||||||
7. |
(arcsin x) |
|
|
|
|
1 |
|
|
(| x | 1) . |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
x2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
8. |
(arccosx) |
|
1 |
|
|
(| x | 1) . |
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||
1 x2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x2 . |
|
|
|||||||||||
9. |
(arctgx) 1 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
x2 . |
|
|
|||||||||
10. (arctgx) 1 |
|
|
|||||||||||||||||
11.(a x ) a x ln a .
12.(ex ) ex .
|
|
|
1 |
|
(x 0) . |
|
|||
|
|
|
|
|
|
||||
13. |
(ln x) |
x |
, |
|
|||||
|
|
||||||||
14. |
(log a x) |
1 |
, (x 0, |
a 0) . |
|||||
|
|||||||||
x ln a |
|||||||||
|
|
|
|
|
|
|
|
||
15.(shx) chx .
16.(chx) shx .
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. |
(thx) ch2 x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
18. |
(cthx) sh 2 x . |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19. |
( Arshx) |
|
x2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(| x | 1), |
|||||||
20. |
( Archx) |
|
x2 1 |
, |
||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
(| x | 1) . |
||||||||
|
|
1 x2 |
|
|
|
|
|
|
||||||||||||||
21. |
( Arthx) |
, |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
x2 |
|
1 |
|
|
|
|
(| x | 1). |
|||||||||||||
22. |
( Arcthx) |
|
|
, |
|
|||||||||||||||||

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
16 |
|
3º. Производная степенно-показательной функции. |
|
|
uv / |
v uv 1 u / uv ln u v/ , |
( 2 ) |
где u u(x),v v(x) - дифференцируемые функции.
4º. Логарифмическая производная
Логарифмической производной функции y f (x) называется производная от логарифма этой функции, т.е.
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
f (x) |
|
||
(ln y) |
y |
f (x) |
( 3 ) |
|||||
|
||||||||
2.2. Вычисление производных
Найти производные функций
Пример 1. y 16 x6 52 x5 53 x3 2x 7 .
Решение. Пользуясь правилами нахождения производной, получим y 16 (x6 ) 52 (x5 ) 53 (x3 ) 2x (7)
Пример 2. |
y x3 cos x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Решение. Применим формулу для производной произведения |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
y |
|
(x |
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3x |
2 |
cosx x |
3 |
sin x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
) cosx x |
|
|
(cosx) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Пример 3. |
y |
2x2 |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
(2x |
|
1) cos x (2x |
1)(cosx) |
|
|
|
2x cos x (2x |
1)sin x |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Решение. y |
|
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
cos2 x |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
y 3 |
|
|
|
|
|
|
2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример 4. |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
1 |
|
|
2 |
|
1 |
|
|
3 |
|
|
2 |
|
|
|
1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Решение. |
y 3 |
x |
|
|
|
|
2 |
|
|
|
|
|
|
x 3 |
|
2 x |
2 |
|
|
|
x 3 |
x |
2 |
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
33 x x x |
|
|
|||||||||||
Пример 5. |
y cos2 x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Решение. |
Это сложная функция, ее можно представить в виде: y u 2 |
|
, где |
|||||||||||||||||||||||||||||||||||||||||||||||||||
u cos x. Тогда по формуле дифференцирования сложной функции, получим y y (u)u (x) 2xcosxsin x sin 2x .
Пример 6. |
y earcsinx |
|
|
|
|
|
|
|
Решение. u arcsin x, |
y eu ; |
y eu u |
earcsinx |
|||||
|
|
|
||||||
|
||||||||
|
|
|
|
|
|
1 x2 |
||
Пример 7. |
y ctg 3 x4 |
5 . |
|
|
|
|
||

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение. |
|
y u3 , u ctgv; |
|
v |
|
w, w x4 |
5. |
|
|
|
|
|
Следовательно, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||
y |
ctg |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x |
|
. |
|||||||||
|
y (u)u (v)v (w)w (x) 3 |
|
|
|
5 |
2 |
|
x |
4 |
|
|
|
x |
4 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
5 |
2 |
|
5 |
|
|
|||||||
Пример 8. |
|
y x3 cos2 x5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Эта функция представляет произведение двух функций, одна из которых – сложная
y (x3 cos2 x5 ) (x3 ) cos2 x5 |
(cos2 x5 ) x3 3x2 cos2 x5 2cos x5 sin x5 5x4 x3 |
|||
3x2 cos2 |
x5 5x7 sin 2x5 x2 |
(3cos2 x5 5x5 sin 2x5 ). |
||
Пример 9. |
y |
sin 3 x |
. |
|
|
|
|||
|
|
ex |
|
|
Решение. Эта функция представляет частное двух функций, одна из которых
– сложная.
|
|
|
|
3 |
|
|
|
|
x |
|
(e |
x |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
3 |
x 3sin |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3cosx) |
|
||||||||||||||
y |
(sin |
|
x) e |
|
|
|
) sin |
|
x |
|
|
e |
|
(sin |
|
|
|
x cos x) |
|
sin |
|
x(sin x |
. |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
e2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ex |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 10. |
|
y arccosx ex2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Решение. y (arccosx) (ex |
2 |
) |
|
|
1 |
|
|
2x ex |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 11. |
|
y arctg |
|
x2 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2x |
|
|
|
|
|
|
|
|
|
|||||||||
Решение. |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
|
|
1) |
|
|
|
|
2x |
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
2 |
|
|
1 x2 |
1 |
2 x2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
x2 |
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Пример 12. |
|
y 1 e2x |
arccosx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2e2 x |
|
|
1 e2 x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
y 1 e2 x |
|
arccosx |
|
|
|
1 e2 x |
(arccosx) |
|
|
|
|
|
|
|
|
|
|
arccosx |
|
|
|
. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 e2 x |
|
|
|
1 x2 |
||||||||||||||||
Пример 13. |
|
y x x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Решение. Логарифмируем по основанию e . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
ln y x ln x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Дифференцируя, находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
y |
|
1 ln x x |
1 |
|
; |
|
|
|
|
|
|
|
|
y |
|
ln x |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
y |
x |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y x x (ln x 1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Пример 14. |
|
|
y xcos x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ln y cosxln x ; |
|
|
|
y |
|
sin x ln x cos x |
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
y |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
|
18 |
|
|
следовательно, |
|
|
|
y xcos x ln xsin x ecos x 1 cosx . |
|
|
|
Пример 15. |
Найти точку, в которой касательная к графику функции |
||
перпендикулярна прямой |
составить уравнение |
||
этой касательной. |
|
|
|
Решение. |
Прямые |
|
|
взаимно перпендикулярны тогда и только тогда, когда |
. |
||
Уравнение касательной к графику функции |
в точке |
имеет |
|
вид: |
|
|
|
Для того, чтобы эта прямая была перпендикулярна прямой |
|
||
необходимо и достаточно, чтобы выполнялось равенство |
Отсюда |
||
находим что касательная, проведенная к графику функции |
|||
перпендикулярна данной прямой только в точке |
.подставляя |
||
значение в уравнение, получим |
|
|
|
Контрольные примеры
1.y (ax b)10 .
3.y (2x2 3)10 .
|
y |
x 1 |
|
5 |
|||||
5. |
|
|
|
|
|
|
|||
|
|
|
|
||||||
|
|
||||||||
|
|
x |
x |
||||||
|
|
1 |
|
|
1 |
|
|||
7. |
y |
|
|
|
|
. |
|||
3cos3 x |
cos x |
||||||||
9. |
y sin 9 (7x 9) |
||||||||
11. |
y cos x5 . |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
||
13. |
y 3 sin 2 |
x |
|
|
|
. |
|||||||
|
|
|
|
|
|
||||||||
|
cos3 x |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
15. |
y 1 arcsin x . |
|
|
||||||||||
17. |
y ln 3 (5x 1) . |
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
1 |
|
|
|
|||
19. |
y ln 1 |
|
|
|
|
|
|
|
. |
|
|||
|
|
|
|
|
|
||||||||
|
|
|
|
x |
|
|
x |
|
|
||||
2. y (ax b) 3 . c
4. y 
 1 x2 .
1 x2 .
6. y 3 x
x 
 x 1
x 1
8. y cos5 (3x 1) .
10. |
y |
|
|
x |
|||||
|
|
|
|
|
|
|
|
||
sin 3x 9 |
|||||||||
|
|
|
|
|
|
|
|
|
|
12. |
y |
|
|
3sin x 2cos x |
. |
||||
5 |
|
||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
||||
14. |
y |
|
sin 2 x 5 |
||||||
16. |
y tg5 (2x2 1) . |
||||||||
|
|
|
|
|
|||||
18. |
y |
|
arctgx (arcsin x)3 . |
||||||
20. |
y ln( x2 1) . |
||||||||

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
19
21. y ln |
|
|
|
|
2 x |
|
. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|||||||||||||
23. |
y arctg |
3x x3 |
. |
|
||||||||||||||||||||||
1 3x2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x3 |
|
|
|
|
|||||||
25. |
y arccos |
|
|
|
|
|
|
|
. |
|
|
|||||||||||||||
|
x2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||
27. |
y arcsin(ln x) . |
|
|
|
|
|||||||||||||||||||||
29. |
y arctg |
|
|
|
3sin |
|
. |
|||||||||||||||||||
|
|
|
||||||||||||||||||||||||
1 x cos |
||||||||||||||||||||||||||
31. |
y ln(arcsin 5x) . |
|
|
|||||||||||||||||||||||
33. |
y |
|
|
arccosx |
|
. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 x2 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
35. |
y arccos |
1 2x . |
||||||||||||||||||||||||
37. y ecos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y 3ctg |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
39. |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
41. |
y xarcsinx . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
43. |
y x ln x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
||||||||||||
45. |
y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
47. |
y x |
|
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
49. |
y x xx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
22. y ln sin 
 xtg
xtg 
 x
x 
 x .
x .
24. y arcctg 1 x .
1 x
26. y 2x tg2x ln cos2x 2x2 .
28. y arcsin(1 x) 
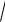 2x x2 .
2x x2 .
|
|
|
|
|
|
|
|
|
5tg |
x |
|
4 |
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
30. |
y |
|
arctg |
|
|
|
|
|
. |
|
|
|
|
|
|||||||||
3 |
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||
32. |
y |
|
|
arcctg |
tgx |
|
x . |
|
|
|
|
|
|||||||||||
|
2 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
34. |
y |
x |
|
|
arcsin |
|
x |
|
|
x x |
|
. |
|||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
36. y sin 2x e2cos2 x .
38. y 101 e x (3sin 3x cos3x)
40. y 2cos2 x 3cos x.
42. y ctgx x3 .
44. y xsinx .
46. y (arctgx)x .
48. y x x 2 .
50. y (cosx)sinx
51. |
Составить уравнение касательной |
к |
графику |
функции |
|
|
в точке с абсциссой |
. |
|
|
|
52. |
Найти на графике функции |
|
|
такую |
точку, в |
которой касательная параллельна прямой |
|
, |
и составить уравнение |
||
этой касательной. |
|
|
|
|
|
2.3.Производные неявных функций
Если дифференцируемая функция y y(x) удовлетворяет уравнению
|
|
|
F(x, y) 0 , |
(4) |
|
то производная |
y |
|
|
этой неявной функции находят, дифференцируя |
|
|
y (x) |
||||
обе части уравнения (4), рассматривая y как функцию от x

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
20
dxd (F(x, y)) 0 .
Пример 1. Найти производную неявной функции x3 y3 3xy 0 . Решение. Дифференцируя, получим
|
|
|
|
|
|
|
3x |
2 |
3y |
2 |
y |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3( y xy ) 0 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 y2 y y xy 0 , |
|
|
|
|
|
|
|
|||||||||||||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
y |
x |
|
y 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, если xln y y ln x 1. |
|
|
|||||||||||||||||
|
Найти yx при x |
|
|
|||||||||||||||||||||||||||||||||
Решение. |
|
|
Это |
|
|
уравнение определяет |
y |
как неявную |
функцию |
x . |
||||||||||||||||||||||||||
Дифференцируем по |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
||
ln y |
|
|
|
y |
y ln x |
|
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
y |
|
x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
y |
x |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
ln x |
|
|
|
|
|
ln y |
0 . |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
ln y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
yx |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Чтобы найти |
|
|
|
|
|
|
|
при |
x 1 необходимо |
еще |
определить |
значение |
y , |
|||||||||||||||||||||||
|
|
|
|
yx |
|
|
||||||||||||||||||||||||||||||
соответствующее данному значению |
x . |
|
|
|
|
|||||||||||||||||||||||||||||||
Подставляя значения x , y в формулу для производной, получим |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
e ln e |
|
, |
|
|
|
|
|
|
|
e 1 |
, |
|
|
1 . |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
yx |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
yx |
|
1 |
|
|
yx e e |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
ln1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
||||||
Пример 3. Вычислить значение производной функции, заданной
неявно |
|
xy 2 |
4 в точке М(1,2). |
|
|||||||
Решение. Найдем производную: y2 2xyy 0 , |
|
||||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
2x . |
|
||||||
|
|
|
|
|
|||||||
Подставляя |
в |
правую часть последнего равенства значение x 1, |
y 2, |
||||||||
получаем |
|
|
|
|
|
|
|
|
|
||
y |
|
|
2 |
|
|
|
|
1. |
|
||
|
|
|
|
|
|
||||||
2 |
1, y |
|
|||||||||
|
|
|
|||||||||
