Полиномы Цернике в проектировании оптических систем. Ч. 1 (96

Московский государственный технический университет имени Н.Э. Баумана

С.Н. Бездидько, Т.С. Ровенская

ПОЛИНОМЫ ЦЕРНИКЕ В ПРОЕКТИРОВАНИИ ОПТИЧЕСКИХ СИСТЕМ

Часть 1

Рекомендовано УМО по образованию в области приборостроения и оптотехники в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению подготовки 200200 «Оптотехника» и специальности 200203 «Оптико-электронные приборы и системы»

М о с к в а Издательство МГТУ им. Н.Э. Баумана

2 0 0 6

УДК 535.317.2(075.8) ББК 22.34

Б39

Рецензенты: В.М. Кахновский, А.Ф. Ширанков

Бездидько С.Н., Ровенская Т.С.

Б39 Полиномы Цернике в проектировании оптических систем: Учеб. пособие. – Ч. 1. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 44 с.: ил.

ISBN 5-7038-2928-3

Описана волновая аберрация оптической системы аппроксимациями по степенному и ортогональному (в виде полиномов Цернике) базисам. Рассмотрены свойства этих аппроксимаций, а также примеры применения разложения волновой аберрации по ортогональным полиномам Цернике для обоснования выбора прототипа из базы оптических систем и для автоматизированной дискретизации областей зрачка и предмета в процессе оптимизации оптической системы.

Для студентов МГТУ им. Н.Э. Баумана, обучающихся по специальности «Оптико-электронные приборы и системы».

Ил. 4. Табл. 10. Библиогр. 31 наим.

УДК 535.317.2(075.8) ББК 22.34

ВВЕДЕНИЕ

Нарушение гомоцентричности прошедшего оптическую систему гомоцентричного пучка лучей или сферичности волнового фронта называется аберрацией.

В зависимости от решаемой оптической задачи используется тот или иной вид описания аберрации. В применении к центрированным осесимметричным системам плодотворным оказалось разложение волновой аберрации по системе круговых полиномов Цернике [1, 2], ортогональных внутри единичного круга [3 – 5]. Позднее появились работы, расширяющие область применения такого разложения на зеркальные и зеркально-линзовые системы [6 – 8], а также на случай полихроматического изображения. В работе [9] описано разложение волновой аберрации оптической системы по ортогональным полиномам при наличии децентрировки на оптической оси.

Данный вид представления волновой аберрации используется при решении многих задач: при вычислении дифракционного интеграла и изучении дифракционной картины в изображении точки при наличии определенных типов аберраций [5]; при установлении зависимостей между различными критериями качества изображения и разложением волновой аберрации или связанными с нею функциями [5, 11 – 16]; при расчете допустимых значений аберраций для широкого класса оптических приборов [5, 10, 13]; при расчете допусков формы оптических поверхностей, центрировки линз и оптических компонентов, определении требований к характеристикам оптического материала [10]; при разработке методов оптимизации оптических систем [17, 18].

Разложение волновой аберрации по полиномам Цернике находит применение при разработке методов и приборов для контроля оптических систем и прозрачных сред, использующих различные параметры волновых фронтов [19]; в офтальмологии при разработке методов и приборов для диагностики и лечебного воздействия на глаз.

3

В данной работе рассматриваются свойства разложения волновой аберрации по полиномам Цернике, полезные для решения актуальных задач автоматизированного расчета оптических систем:

–для автоматизированного определения оптимальной дискретизации областей зрачка и предмета на этапах оптимизации оптической системы;

–для автоматизированного выбора базовой схемы (прототипа) проектируемой оптической системы из базы данных конструктивных параметров оптических систем и аберрационного анализа базовой схемы.

1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Лучевая аберрация отдельного луча гомоцентричного в пространстве предметов пучка характеризуется вектором обобщенных

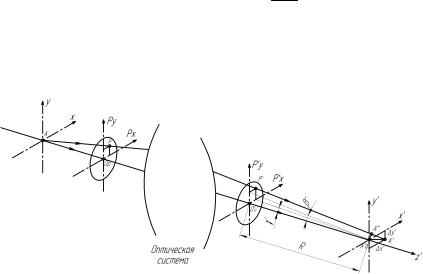
ки А′ пересечения луча Р′A′ с поверхностью изображения, определенные в прямоугольной системе зональных координат (x′, y′, z′) с началом в точке идеального изображения А0′; P(px, py), P′(p′x, p′y) – точки пересечения луча, выходящего из точки А предмета, с плоскостями

входного и выходного зрачков оптической системы; отрезок Α0′ Α′ есть лучевая поперечная аберрация (рис. 1). Проекции ∆y′, ∆x′ вектора Α0′ Α′ на оси y′ и x′ соответственно называются меридиональной и сагиттальной составляющими поперечной аберрации. Для удаленного изображения ∆X ′ = q0′ − q′ понимается как угловые отклонения

реального луча q′ от идеального q0′, соединяющего точку P′ луча на выходномзрачкесточкойидеальногоизображения.

Волновая аберрация V описывает отклонение выходящего волнового фронта от сферы сравнения вдоль данного луча. Если через

центр O′p′ выходного зрачка оптической системы (см. рис. 1) построить сферическую поверхность с центром в точке А0′, то будет

тим перпендикуляр А0′ А′′ на луч Р′A′, где А′′ – основание перпен-

4

дикуляра. Монохроматическая волновая аберрация V для луча AA′ понимается как разность оптических длин хода лучей

V = ‹ AA′ › – ‹ AA′′ ›; V = n′λ∆l ,

где ∆l = A′′A′; n′ – показатель преломления среды пространства изображений; λ – длина волны.

Рис. 1. Определениелучевойиволновойаберрацийоптическойсистемы

Путем расчета волновой аберрации для множества лучей, исходящих из точки A и проходящих через входной зрачок оптической системы, определяется волновая поверхность, или волновой фронт.

Лучевая и волновая аберрации являются функциями зрачковых координат луча:

∆x ′ = ∆x ′( p); V =V ( p)

или

∆x ′ = ∆x ′( p′); V =V ( p′),

определяются как координаты точек Р и Р′ пересечения луча с

5

входной или выходной сферами сравнения, или опорными сферами Гаусса, концентричными точке предмета А и точке A0′ ее идеального изображения. Координаты p, p′ задаются как линейные или угловые в зависимости от типа предмета и изображения [20].

Между лучевой ∆X ′ и волновой V аберрациями луча существует связь: поперечные аберрации с точностью до постоянных множителей являются частными производными волновой аберрации по координатам луча на зрачке. Это отражается уравнениями

или

∆X ′ = −λ V ( p′),

где λ – длина волны; величина V задается в длинах волн.

Анализ работы оптической системы принято проводить не в реальных зрачковых координатах p, p′ и координатах на предме-

Здесь через А и А′ обозначены обобщенные передние и зад-

ние апертуры, которые в обобщенных зрачковых координатах для виньетированных зрачков представляют собой полуоси эллипти-

ют вид круга единичного радиуса: ρ = ρ′ =1.

Канонические, или приведенные, координаты на предмете η и изображении η′ в [20] определены выражениями

Для описания воздействия оптической системы на проходящий через нее пучок лучей или волновой фронт используется зрачковая функция

1

f (ρ) = τ2 (ρ) exp[−2πiV (ρ)] в пределах единичного круга,

0 вне круга,

где τ(ρ) − функция пропускания энергии, 0 < τ < 1.

Зрачковая функция используется при определении функции рассеяния точки (ФРТ), оптической передаточной функции (ОПФ) и связанных с этими функциями критериев качества оптического изображения. Понятия ФРТ, ОПФ и критерии качества изображения позволяют решать как прямые задачи оценки качества изображения в известной оптической системе (и оценивать допуски на параметры оптической системы), так и обратные задачи, на-

7

пример определять допустимые значения аберраций в оптических системах, исходя из определенного критерия качества для оптических систем различного функционального назначения [10].

2. ОПИСАНИЕ ВОЛНОВОЙ АБЕРРАЦИИ

Для решения задач, связанных с проектированием оптических систем, необходимо численное описание функции волновой аберрации. Чаще всего монохроматическую функцию V (ρ) описывают

в виде разложения от канонических зрачковых координат

где Pk (ρ) – функция базиса; ρ − вектор канонических координат

на зрачке; Сk – коэффициенты аппроксимации.

Для разложения (2) чаще всего применяют полярные коорди-

наты ρ = ρ = ρ2x +ρ2y ; cosϕ = ρρy , а в качестве базиса используют степенные функции или ортогональные полиномы Цернике.

2.1. Зональное монохроматическое описание волновой аберрации

Разложение волновой аберрации по степенному базису состоит

где n ≥ m; n + m = 2k – четное; n, m – числа натурального ряда. Значения коэффициентов wnm равны значению волновой абер-

рации данного типа на краю зрачка: ρ = 1, φ = 0.

Классификация отдельных зональных аберраций Wnmρn cosm ϕ, составляющих волновую аберрацию V (ρ) , дана в табл. 1.

8

При разложении волновой аберрации по ортогональному базису в виде круговых полиномов Цернике используют условие орто-

гональности.

Оно означает, что интеграл по зрачку от произведения двух различных функций базиса

где δkl – символ Кронекера, т. е. дискретная дельта-функция,

Qkm (t) – полином от t степени k, являются полиномами по основа-

нию ρ, содержащими степени ρn, ρn–2, …, ρm, и связаны с полиномами Якоби (вырожденными гипергеометрическими функциями). Радиальные полиномы определяются формулами

9

Rnm (1) =1.

Для вычисления значений радиальных полиномов Цернике может использоваться их связь с гипергеометрической функцией

F(a, b, c, z):

Применяя схему Горнера, окончательное выражение для вычисления значений радиальных полиномов получают в виде [21]

Изортогональностиполиномов Rnm (ρ) и Qkm (t) следуютвыражения

10