Лабораторные работы и методические указания по теме Функции многих переменных (110

функции u:

1:

u = x2 cos y + 3yz2

2:

u = xy2 ¡ 5y tg x

3:

u = (xy ¡ x + y)ex+y

4:

u = (x + 2y)4 ¡ z sin y

5: u = ln(x + 3z) ¡ y4 + zy

6:

u = cos xy ¡ yp

z

7:

u = sin x ¢ sin(3y + x)

8:

u = (x2 + y3)2 ¡ 3x

9:

u = sin(5x + y2) ¡ z ln y

10: u = xey ¡ yex

11: u = cos(x ¡ y2) ¡ zx2

12: u = exy ¡ zx2

13: u = y2(3x ¡ 2y)

14: u = e4y¡5x ¡ x tg y

15: u = sin x + sin(zy2)

16: u = ln(x ¡ 3y) + z2 sin x

9:

x2 + zx + z2 + y = 0

10: z ¡ x =

y

tg (z

¡

x)

11:

x + y + z = ln (xyz)

12:

x ¡ z = z ln

µy

¶

z

13:

x3 + y3 ¡ 3xyz ¡ z3 = 1

14:

z3 ¡ xz + y = 0

уравнения:

1: y00(y0)¡3 ¡ x = 0;

x = x(y)

2:

y00 + (ey ¡ x)(y0)3 = 0;

x = x(y)

3:

y0y000 ¡ 3(y00)2 = 0;

x = x(y)

15: xyy00 ¡ x(y0)2 + yy0 = 0; u = ln ³

y

´;

t = y;

u = u(t)

x

16: y00 =

y

; u =

y

; t = ln

x ¡ 1

; u = u(t)

(x ¡ 1)2(x ¡ 2)2

x ¡ 2

x + 2

Задание 3. Приняв u и v за новые независимые переменные

функции z, выразить через них частные производные zx0 ; zy0 :

1:

u = xp

y; v = ey ln x

2:

x = u cos v; y = u sin v

x

3:

u = ln µ

¶;

v = p

4:

x = cos u; y = cos v

y

y

1

1

x = (u + v)2; y = (u ¡ v)2

5:

u = ln xy; v = p

+ p

6:

x

y

7:

u =

1

; v = xy2

8:

x = arctg (uv); y = u=v

x2

9: u = x ¡ 2p

y; v = x + 2p

10: x = u; y = uv

y

1

1

u

11:

u =

+ 2y; v =

+ 2x

12:

x = ln pu2 + v2; y= arctg ³

´

x

y

v

13:

u = xy; v = xy3

14:

x = uev; y = veu

x

15:

u = y tg ³

´; v = y

16:

x = sin u; y = sin v

2

Задание 4. Приняв u и v за новые независимые переменные, пре-

образовать следующие уравнения:

@2z @2z

1:

¡

= 0; u = x ¡ y; v = x + y

@x2

@y2

2:

@2z

+ y

@2z

+

1

@z

= 0; u = x; v = 2p

(y > 0)

y

@x2

@y2

2 @y

@2z

@2z

@2z @z

1

1

3:

2

¡ 2

+ 5

¡

= 0;

u =

(x ¡ y); v =

(2x + y)

@x2

@x@y

@y2

@x

3

3

@2z

@2z

¡ 3

@2z

@z

@z

u = x + y; v = 3x ¡ y

4:

+ 2

+ 2

+ 6

= 0;

@x2

@x@y

@y2

@x

@y

@2z

@2z

@2z

@z

@z

u = 2x ¡ y; v = x

5:

+ 4

+ 5

+

+ 2

= 0;

@x2

@x@y

@y2

@x

@y

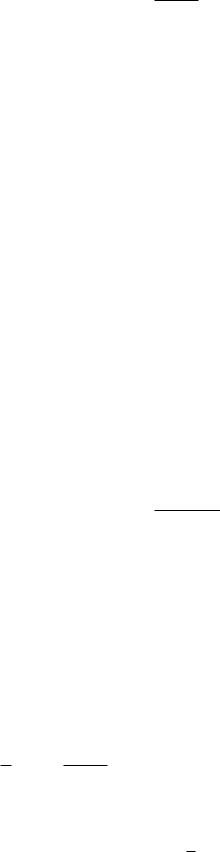
6:

@2z

4

@2z

= 0; y =

u + v

; x =

u ¡ v

@x2 ¡

@y2

2

4

2

@2z

2

@2z

@z

y

7: x

¡ y

¡ 2y

= 0; u = xy; v =

@x2

@y2

@y

x

2

@2z

¡ 2x

@2z

@2z

y

8:

x

+

= 0;

u = xe

; v = y

@x2

@x@y

@y2

9:

x

2

@2z

¡ 2xy

@2z

¡ 3y

2 @2z

= 0;

u =

y

; v = yx

3

@x2

@x@y

@y2

x

10: x

2

@2z

+ 2xy

@2z

+ y

2

@2z

= 0; u =

y

; v = y

@x2

@x@y

@y2

x

@2z

@2z

+ (2 ¡ cos2 x)

@2z

11:

¡ 2 sin x

= 0;

u = x; v = y ¡ cos x

@x2

@x@y

@y2

2

@2z

¡ 2y tg x

@2z

2 @2z

3

@z

12: tg

x

+ y

+ tg

x

= 0; u = y sin x; v = y

@x2

@x@y

@y2

@x

@2z

2p

@2z

@2z

1

@z

= 0; u = p

+ p

; v = p

13: x

+ y

+

x

x

xy

y

@x2 ¡

@x@y

@y2

2 @y

14: y

2 @2z

+ 2y

@2z

+

@2z

= 0; y = v; x =

u + v2

@x2

@x@y

@y2

2

15:

@2z

¡

y

@2z

= 0; x =

u + v

; y =

(v ¡ u)2

(y > 0)

@x2

@y2

2

16

@2z

@2z

16:

+

+ m2z = 0; 2x = u2 ¡ v2; y = uv

@x2

@y2

14: (1 ¡ x2)zxx00

+ (1 ¡ y2)zyy00

= xzx0 + yzy0 ;

если x = cos u; y = cos v; z = ew

15: y2zxx00 = (x + y)zyy00 ;

если

u = 2x; v = x ¡ y; w = 2x

¡

2y + 4z

2

16: (1 ¡ x)zxx00 ¡ zyy00 ¡ zx0 = 0;

p

если u =

y

p

y

p

p4

+

1 ¡ x; v =

¡

1 ¡ x; w =

2z

1 ¡ x

2

2

Лабораторная работа № 4

Экстремум функции многих переменных

Задание 1.

Найти экстремумы функции, заданной следующим

уравнением:

1:

u =

ax + by + c

; a2 + b2

+ c2

> 0

2:

u = xy +

a

+

b

1 + x2 + y2

x

y

3:

p2

¡ xy + 2xz ¡ y + y

3

+ z

2

4:

u = x

2

¡ 2xy + 4y

3

u = 2x

5:

u = x2 + 3xy ¡ 8 ln jxj ¡ 6 ln jyj

6: u = 3x2y ¡ x3 ¡ y4

7: u = x2 ¡ xy + y2 ¡ 2x + y

8:

u = ex+2y(x2 ¡ y2)

9: u = ex¡y(x2 ¡ 2xy + 2y2)

10: u = x3 + y3 + 3axy

11: u = (x2 + 2y2)e¡(x2+y2)

12: u = x4 + y4 ¡ 36xy

13: u = x3 ¡ 2y3 ¡ 3x + 6y

14: u = 4 ¡ (x2 + y2)32

15: u = x +

y2

+

z2

+

2

; x > 0; y > 0; z > 0 16: u = xy +

1

4x

y

z

2(x + y)

Задание 2.

Исследовать функцию на условный экстремум:

¼

¼

1:

u = x ¡ y;

если tg x ¡ 3 tg y = 0; jxj <

; jyj <

2

2

2:

u = xyz;

если xy + xz + yz = 9; x > 0; y > 0; z > 0

3:

u = xy2z3;

если x + 2y2 + 3z3 = 1; x > 0; y > 0; z > 0

4:

u = xy + yz

если x2 + y2 = 2; y + z = 2; x > 0; y > 0; z > 0

1

1

1

1

1

5:

u = 1 +

+

; если

+

=

x

y

x2

y2

8

6:

u = 2x + y ¡ z + 1;

если x2 + y2 + 2z2 = 22

7:

u = xy2;

если x + 2y = 1

8:

u = 5 ¡ 3x ¡ 4y; если x2 + y2 = 25

9:

u = xy + 2xz + 2yz;

если xyz = 108

10:

u = x ¡ 2y + z; если x + y2 ¡ z2 = 1

11:

u = x2 + y2 + 2z2; если x ¡ y + z = 1

12:

u = x3 + y2 ¡ z3 + 5;

если x + y ¡ z = 0

13:

u = x2 ¡ y2;

если

x

+

y

= 1

a

b

14:

u = x ¡ y + 2z; если x2 + y2 + 2z2 = 16

15:

u = xy; если x3 + y3 ¡ 3xy = 0

16:

u = ln (xy);

если x3 + xy + y3 = 0

2

-2

0

2

y•=-2x

x•+y•=4

-2

x!0 y!0

y!0 x!0

б) Вычислить двойной предел

lim u(x; y) или доказать, что он

x!0

не существует.

y!0

x2y2

u =

:

x2y2 + (x ¡ y)2

lim lim u(x; y) = lim

lim

x2y2

Решение: Вычислим x!0 y!0

x!0 ½y!0 x2y2 + (x ¡ y)2 ¾.

Так как для любого x 6= 0 внутренний предел

lim

x2y2

=

x2 ¢ 0

=

0

= 0;

x2 ¢ 0 + (x ¡ 0)2

x2

y!0 x2y2 + (x ¡ y)2

то lim lim u(x; y) = lim 0 = 0:

x!0 y!0

x!0

x2y2

¾. Так как для

lim lim u(x; y) = lim

lim

Вычислим y!0 x!0

y!0

½x!0 x2y2 + (x ¡ y)2

любого y 6= 0 внутренний предел