Моделирование процессов с нелинейностями гистерезисного типа (110

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

МОДЕЛИРОВАНИЕ ПРОЦЕССОВ С НЕЛИНЕЙНОСТЯМИ ГИСТЕРЕЗИСНОГО ТИПА

Составители: М. Б. Зверева, М. И. Каменский, Е. В. Рачинский

Учебно-методическое пособие

Воронеж Издательский дом ВГУ

2016

Содержание

3

§1. Функции ограниченной вариации

Пусть H гильбертово пространство (ГП), т.е. в H определено скалярное произведение, и H является полным по норме, порождаемой

!

Функция u(t) называется функцией ограниченной вариации, если существует константа C такая, что для любого разбиения отрезка [a; b]

где sup берется по всевозможным разбиениям отрезка [a; b].

Пример 1.1. Если функция u: [0; T ] ! H удовлетворяет условию Липшица с константой L > 0, т.е. для любых t; s 2 [0; T ] верно ku(t) u(s)k 6 L jt sj, то u(x) является функцией ограниченной вариации,

причем Var(u) 6 L T .

В самом деле, для любого разбиения отрезка [0; T ] верно

P

Следовательно, Var(u) = sup ku(ti+1) u(ti)k 6 L T .

i=0

Заметим, что непрерывная функция, вообще говоря, не является функцией ограниченной вариации. В качестве примера рассмотрим функцию

4

которая, как нетрудно видеть, непрерывна на отрезке [0; 2]. Для разбие-

a это число может быть сделано сколь угодно большим за счет выбора

Из определения следует, что множество функций ограниченной ва-

риации образует линейное пространство, т.е. верны следующие свойства.

1.Если постоянное число, то V ar( f) = j jV ar(f):

2.Если f, g функции ограниченной вариации, то f + g тоже является функцией ограниченной вариации, и V ar(f + g) 6 V ar(f) + V ar(g):

Теорема 1. Пусть H ГП, un последовательность функций un : [0; T ] ! H таких, что 8 n 2 N kun(t)k 6 M1, Var(un) 6 M2. Тогда существует подпоследовательность unk , слабо сходящаяся в H для

hunk (t); zi ! hu(t); zi при k ! 1. При этом Var(u) 6 M2.

Предлагаем доказать в качестве упражнения.

Про слабую сходимость нам в дальнейшем потребуется следующий

факт. (Предлагаем доказать в качестве упражнения.)

слабо

Лемма 1. Пусть un ! u. Тогда

n!1

а) kuk 6 lim kunk.

n!1

б) Если un 2 C + B"n (0), где B"n (0) замкнутый шар с центром

в 0 и радиусом "n, C H замкнутое выпуклое множество,

"n ! 0, то u 2 C.

n!1

5

Упражнения.

1.1Докажите, что всякая функция ограниченной вариации ограничена.

1.2u(t) = const , Var(u) = 0.

1.3Пусть u: [0; T ] ! R, u(t) монотонная функция. Докажите, что u(t) является функцией ограниченной вариации, причем Var(u) = ju(T ) u(0)j.

1.4Пусть u: [0; T ] ! R является функцией ограниченной вариации. Тогда u(t) = u1(t) u2(t), где функции u1(t) и u2(t) не убывают на

[0; T ].

1.5Пусть функция u(t) представляет собой ломаную в гильбертовом

пространстве, т.е. существуют точки 0 = t0 < t1 < : : : < tN =

:

не является функцией ограниченной вариации на [0; 1].

1.7Покажите, что произведение двух функций f и g ограниченной вариации есть снова функция ограниченной вариации, причем

6

§2. Некоторые сведения из выпуклого анализа

Пусть C H(ГП) замкнутое выпуклое множество.

Напомним, что множество C называется замкнутым, если оно содержит все свои предельные точки.

Множество C выпуклое, если 8 x, y 2 C : отрезок [x; y] C, где отрезок [x; y] в ГП определяется как множество

[x; y] = f x + (1 )y; 2 [0; 1]g:

Пусть x 2 C. Конусом нормалей в точке x ко множеству C будем называть множество

NC(x) = f 2 H : h ; c xi 6 0 8c 2 Cg:

Заметим, что если x 2 H, и C H замкнутое выпуклое множество, то существует единственный y 2 C, минимизирующий расстояние от точки x до множества C: (dist(x; C)), где

dist(x; C) = inffkx ck : c 2 Cg:

Такой элемент y называется проекцией элемента x на множество C и

обозначается y = proj(x; C). Таким образом,

y = proj(x; C) , kx yk = dist(x; C):

Пусть C1 и C2 выпуклые замкнутые множества в H ГП. Тогда хаусдорфовым расстоянием h(C1; C2) между C1 и C2 называется

h(C1; C2) = maxfsup dist(x; C1); sup dist(x; C2)g:

x2C2 x2C1

Теорема 2. Пусть [x1; x2] отрезок в H (ГП). Функция l : [a; b]

R1 ! H непрерывная и имеет ограниченную вариацию, причем Var(l) 6

7

kx1 x2k + , где > 0. Пусть l(a) = y1; l(b) = y2, и ky1 x1k 6 ; ky2 x2k 6 , > 0; > 0 и + + 6 1. Тогда хаусдорфово расстояние удовлетворяет неравенству

p

h(l; [x1; x2]) 6 (3 + kx1 x2k) + + :

Доказательство. Рассмотрим сначала случай, когда = = 0. Тогда y1 = x1, y2 = x2. Покажем, что для любой точки z 2 l расстояние до [x1; x2] удовлетворяет неравенству dist(z; [x1; x2]) 6 (1+kx1 x2k)p .

Введем обозначения: [x1; x2] = S, kx1 x2k = jSj. Требуется доказать, что dist(z; S) 6 (1+jSj)p для всех z 2 l. Предположим противное, т.е. что найдется z0 2 l такой, что dist(z0; S) > (1 + jSj)p .

Рассмотрим следующие случаи:

а) Пусть на S ближайшей к точке z0 окажется x1. Заметим, что Var(l) > kx1 z0k + kz0 x2k > (1 + jSj)p + jSj > + jSj, поскольку

0 6 6 1. Но по условию Var(l) 6 + jSj. Получили противоречие. Аналогично может быть рассмотрен случай, когда x2 ближайшая к z0.

б) Пусть x0 проекция z0 на множество S. Тогда dist(z0; S) = kz0 x0k, и следовательно, kz0 x0k2 > (1+jSj)2 > +2jSj > 2 +2 kxi x0k.

Поскольку

XX

то получаем противоречие с тем фактом, что Var(l) 6 + jSj, > 0.

p

Таким образом, sup dist(z; [x1; x2]) 6 (1 + kx1 x2k) .

z2l

С другой стороны, заметим, что любой элемент x0 2 S является

ортогональной проекцией некоторого z0 2 l. Более того, dist(x0; l) 6 kx0

p z0k = dist(z0; S) 6 (1 + jSj) .

8

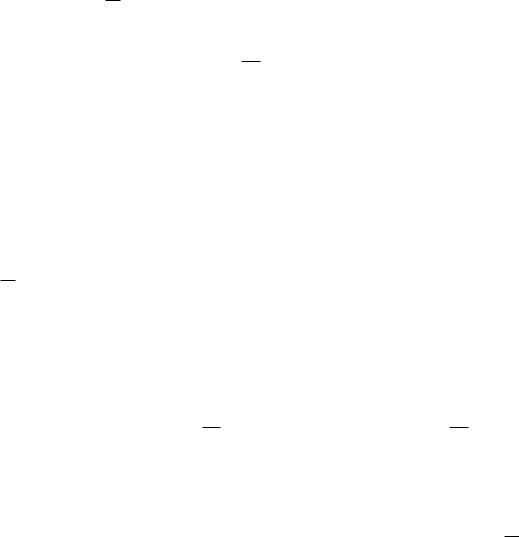
что и требовалось доказать.

Теорема 4. Пусть C замкнутое выпуклое множество в H

ГП, причем B(a; r) C. Тогда для всех x 2 H верно

kx proj(x; C)k 6 21r kx ak2 kproj(x; C) ak2 :

Доказательство. Рассмотрим отображение S(x) = proj(x; C). Оно является сжимающим (докажите в качестве упражнения!). Применив

предыдущую теорему, получим требуемое.

Теорема 5. Пусть C1; C2; : : : ; Cn замкнутые выпуклые множества в H ГП, причем все они содержат в себе замкнутый шар

B(a; r) (r > 0). Тогда, если x0 2 H и точки x1; x2; : : : ; xn такие, что

xi = proj(xi 1; Ci), то

kx0 ak > kx1 ak > : : : > kxn ak;

n

Xkxi xi 1k 6 21r kx0 ak2 kxn ak2 6 21rkx0 ak2:

i=1

Доказательство. Заметим, что kx1 ak = kproj(x0; C1) proj(a; C1)k 6

6 kx0 ak, поскольку отображение proj является сжимающим. Аналогично, kxn ak 6 kx0 ak. По предыдущей теореме, в силу B(a; r) Ci

для всех i = 1; : : : ; n, имеем

Упражнения

Пусть H = R2, C = f(x; 0) : 0 6 x 6 1g (для номеров 2.1 2.3). 2.1 Покажите, что NC((0; 0)) = f( 1; 2) : 1 6 0; 2 2 Rg.

10