Изучение магнитной цепи (120

где J — намагниченность вещества. В вакууме J = 0, поэтому H = B /μ0.

Теорема о циркуляции вектора H в вакууме. Вектор H обла-

дает важным свойством: циркуляция вектора H (интеграл по замкнутому контуру) равна алгебраической сумме токов проводимости, охватываемых контуром:

Все вещества подразделяют на сильные и слабые магнетики. В слабых магнетиках

J = κH,

где κ — характеристика вещества, называемая его магнитной восприимчивостью. Тогда из (4) следует, что

где μ = 1+ κ — магнитная проницаемость вещества.

Значение магнитной проницаемости μ зависит от рода вещества и температуры. Слабые магнетики подразделяют на парамагнетики (μ > 1) и диамагнетики (μ < 1). Значение магнитной проницаемости для пара- и диамагнетиков очень мало отличается от единицы, например: для хлористого железа μ = 1,00250, а для висмута μ = 0,99983.

К сильным магнетикам относятся ферромагнетики: железо и его сплавы, никель, кобальт и др.

Характерной особенностью ферромагнетиков является сложная нелинейная зависимость J(H) и B(H) (рис. 6). Зависимость J(H) показана схематически на рис. 6, а. Уже при сравнительно небольшой напряженности H намагниченностьдостигает насыщения Jнас.

С увеличением напряженности H магнитного поля магнитная индукция B возрастает (см. формулу (6) и рис. 6, б). При малых значениях напряженности H магнитного поля основной вклад в

11

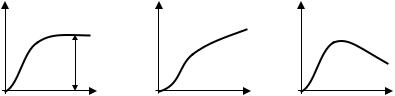
магнитную индукцию B вносит намагниченность J, поэтому сильное магнитное поле в железе получают с помощью небольших токов в катушках с малой затратой электрической энергии. Однако если значение намагниченности J достигает значения насыщения Jнас, то увеличивать магнитную индукцию B становится трудно, для этого необходимо сильно увеличивать ток намагничивающих катушек, т. е. повышать напряженность магнитного поля H.

Рис. 6. Зависимость намагниченности (а), магнитной индукции (б) и магнитной проницаемости (в) от напряженности магнитного поля для ферромагнетика

Магнитная проницаемость ферромагнетика

рассчитанная по формуле (6), не является постоянной величиной, она зависит от напряженности магнитного поля H (рис. 6, в). Несмотря на это, величину μ широко используют для характеристики ферромагнетика. Поскольку величина μ не является константой (зависит от намагничивающего тока), применять ее надо с большой осторожностью. Более полной и надежной характеристикой ферромагнетика служит зависимость B(H) (см. рис. 6, б).

5. Расчет магнитного поля тороидальной катушки с ферромагнетиком

Основными ферромагнитными материалами для электротехники служат специальные сплавы железа. Для расчетного задания

12

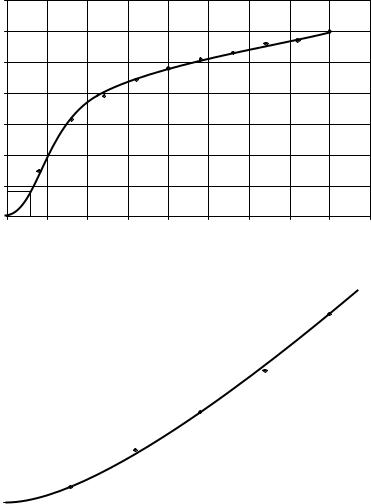
используем зависимость B(H) для электротехнической стали марки ВПТ (табл. 1, рис. 7 [4]). Эта сталь относится к магнитомягким ферромагнетикам, для которых гистерезис (зависимость намагниченности от предыдущего состояния ферромагнетика) выражен слабо [1—3]. Такие материалы используются в переменных магнитных полях трансформаторов и других устройств.

Таблица 1

Зависимость значений намагниченности B

от значений напряженности H магнитного поля для электротехнической стали марки ВПТ

На тороид с длиной средней линии L, изготовленный из ферромагнетика, намотано N витков (см. рис. 4). В изотропном материале векторы H и B имеют одинаковые направления (см. формулу (6)), поэтому внутри тороида линии векторов H и B совпадают; в данном случае эти линии являются окружностями.

Для нахождения напряженности магнитного поля H применим теорему о циркуляции (см. формулу (5)) к окружности длиной L:

v∫ Hl dl = NI ,

где v∫ Hl dl = HL.

Отсюда получим формулу для расчета напряженности магнитного поля:

Для расчета магнитной индукции используем данные, приведенные в табл. 1 и на рис. 7.

В первой строке табл. 2 даны результаты расчета для варианта 1. Расчеты для других вариантов студенты выполняют самостоятельно.

13

B, Тл

1,2

1,0

0,8

0,6

0,4

0,2 0,0

б

Рис. 7. Зависимость значений намагниченности B от значений напряженности H магнитного поля для электротехнической стали марки ВПТ:

а — для сильного поля; б — для слабого поля

14

7.Расчет магнитной цепи

Влабораторной установке для изучения магнитной цепи используется магнитная цепь, изготовленная из железного магнитопровода от трансформатора [5]. Магнитопровод состоит из двух П- образных частей сечением S и длиной средней линии L (рис. 9, S и

L на рис. не показаны). Поверхности стыков этих частей отшлифованы. Раздвигая обе части магнитопровода, создают два зазора* длиной l каждый. На железный магнитопровод намотаны две обмотки. Ток в намагничивающей обмотке I, содержащей N витков, создает магнитное поле. Измерительная обмотка II служит для измерения магнитной индукции в железе.

l Железный магнитопровод

Рис. 9. Схема лабораторной установки для изучения магнитной цепи:

I — намагничивающая обмотка, содержащая N витков; II — измерительная обмотка, содержащая n витков; Г — генератор переменного тока; R — переменный резистор для точной регулировки тока; l — длина зазора; V — вольтметр; mA — миллиамперметр

* Зазор может быть воздушным или заполнен немагнитным материалом.

16

Применяя теорему о циркуляции вектора H (см. формулу (5)) к средней линии магнитной цепи с двумя зазорами длиной l каждый, получаем соотношение

где H — напряженность магнитного поля внутри железного магнитопровода; H1 — напряженность магнитного поля в зазорах.

Выразим напряженности магнитного поля H и H1 через магнитную индукцию B в железном магнитопроводе с магнитной проницаемостью μ и через магнитную индукцию B1 в зазорах с μ = 1:

H = μμB0 ;

H1 = B1 .

μ0

Тогда выражение (9) примет вид

LB + 2lB1 = NI,

μμ0 μ0

или

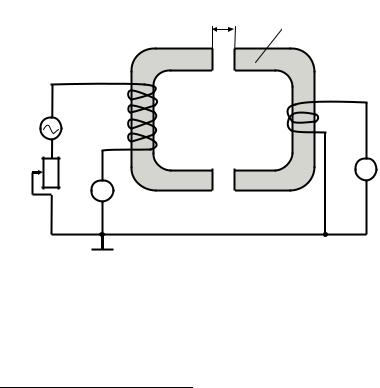
Магнитный поток в зазорах испытывает рассеяние (рис. 10). Если длина l зазора мала по сравнению с поперечным размером магнитопровода (см. рис. 10, а), то рассеяние незначительное и магнитная индукция в зазоре и в железном магнитопроводе одинаковая:

B= B1.

Вэтом случае выражение (10) принимает вид

В зазорах большой длины (см. рис. 10, б) рассеяние велико, поэтому

B1 < B,

причем это различие возрастает с увеличением зазора.

B

аб

Рис. 10. Рассеяние магнитного потока в зазорах различной длины l железного магнитопровода

Влабораторной работе проверяют справедливость формулы (11). При различной длине l зазора устанавливают такой ток I в обмотке, чтобы магнитная индукция B в железном магнитопроводе оставалась постоянной. При этом постоянной будет и магнитная проницаемость μ. По результатам измерений строят графическую зависимость I от l и сравнивают ее с формулой (11).

8.Методика измерения магнитной индукции

Влабораторной работе для измерения магнитной индукции B в железном магнитопроводе используют явление электромагнитной индукции (см. рис. 9). На железный магнитопровод намотана измерительная обмотка II, содержащая n витков. Вольтметр V с большим сопротивлением, подключенный к измерительной обмотке II, измеряет ЭДС индукции. Индукционный ток в этой обмотке мал и не влияет на магнитное поле.

18

Выбранный метод измерения индукции требует применения переменного тока для создания переменного магнитного поля. Источником переменного тока служит электронный прибор — генератор переменного тока Г, в котором частоту и амплитуду тока можно изменять. Дополнительную, более точную регулировку тока проводят с помощью переменного резистора R (см. рис. 9). Силу тока намагничивающей обмотки I измеряют миллиамперметром mA.

Рассмотрим методику измерения магнитной индукции. Переменный ток циклической частотой ω создает в железном магнитопроводе магнитное поле, индукция которого (среднее значение по сечению) изменяется по закону

B = Bmax cos ωt.

Измерительную обмотку II пронизывает полный магнитный поток

Ψ = nS Bmax cos ωt,

где S — площадь поперечного сечения магнитопровода. В измерительной обмотке II возникает ЭДС индукции, равная (см. формулу (2))

ε = − ddtΨ = nSωBmax sin ωt =εmax sin ωt,

где εmax = nSωBmax — амплитуда ЭДС. Из последнего выражения получаем соотношение

Bmax = εnSmaxω.

Принимаем во внимание, что используемые в лабораторной работе приборы измеряют не амплитудные, а действующие значе-

значения всех величин (I, εmax и Bmax) в приведенных выше формулах действующими. Следовательно, магнитную индукцию вычисляют по формуле

19

где ε — действующее значение ЭДС; B — значение магнитной индукции, соответствующее действующему значению силы тока I в формуле (11) для магнитной цепи.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

1. Выполнение лабораторной работы

Задание 1. Ознакомиться с лабораторной установкой и подготовить ее к работе.

Лабораторная установка включает в себя магнитную цепь, генератор переменного тока, миллиамперметр mA и вольтметр V, выполненные в виде цифрового прибора АМ-1109 (см. рис. 9).

Одна часть железного магнитопровода закреплена, а другую можно перемещать. Между двумя частями магнитопровода вставляют пластину толщиной l из немагнитного и непроводящего материала и прижимают обе части магнитопровода друг к другу; такая магнитная цепь эквивалентна цепи с двумя воздушными зазорами длиной l каждый. К лабораторной установке прилагается набор пластин различной толщиной, указанной на пластине.

Магнитная цепь содержит две обмотки: намагничивающую обмотку I и измерительную обмотку II. Через намагничивающую обмотку I пропускают переменный ток от генератора Г. Силу тока измеряют миллиамперметром mA. Электродвижущую силу в измерительной обмотке II измеряют вольтметром V — цифровым прибором АМ-1109, имеющим два канала измерения: СН1 и СН2. Ток измеряют в канале CH2, которому соответствуют верхний переключатель и верхняя строка индикатора цифрового прибора АМ-1109. Электродвижущую силу измеряют в канале CH1 (ему соответствуют нижний переключатель и нижняя строка индикатора цифрового прибора АМ-1109).

К цифровому прибору АМ-1109 должны быть подключены три провода: общий провод черного цвета — к гнезду COM; провод с

20