Теорема (связь между бесконечно малыми и бесконечно большими величинами).
(1) Если α (x) – бесконечно малая, то 1/ α (x) бесконечно большая.
-
Если β (x) – бесконечно большая, то 1/ β (x) бесконечно малая.
Доказательство.
(1) Выберем M > 0 и обозначим 1/ M = ε. Так
как α (x) бесконечно малая, то числу ε >
0 соответствует δ > 0 такое, что при 0 <
|x-a| < δ выполняется неравенство:
Следовательно,
Эта
величина является бесконечно большой.
(2) Выберем ε > 0 и обозначим 1/ε = М. Так
как β(х) бесконечно большая, то числу M
соответствует δ > 0, такое, что при 0 <
|x-a| < δ выполняется неравенство:
Следовательно,
Эта
величина является бесконечно большой.
-
Теорема о пределе суммы, произведения и частного функции (доказательство для функции и последовательности).
1)Предел
суммы двух функций равен сумме их
пределов:
Доказательство:
Пусть
,
.
Тогда по теореме о связи функции, её
предела и бесконечно малой функции
можно записать:
и
.
Следовательно,
,
где
- бесконечно малая функция (по свойству
бесконечно малых функций). Тогда по
теореме о связи функции, её предела и
бесконечно малой функции можно записать
,
или
.
2)Предел
произведения двух функций равен
произведению их пределов:
.
Доказательство:
Пусть
,
.
Тогда
и
.
Следовательно
,
.
Выражения
в скобках, по свойствам бесконечно малых
функций, - бесконечно малая функция.
Тогда
,
т.е.
.
3)Предел
частного двух функций равен пределу
делимого,
деленного на предел делителя, если
предел делителя не равен:
.
Доказательство:
Пусть
,
.
Тогда
и
. Тогда
.
По свойствам бесконечно малых функций,
второе слагаемое – бесконечно малая
функция.
Поэтому
,
т.е.
-
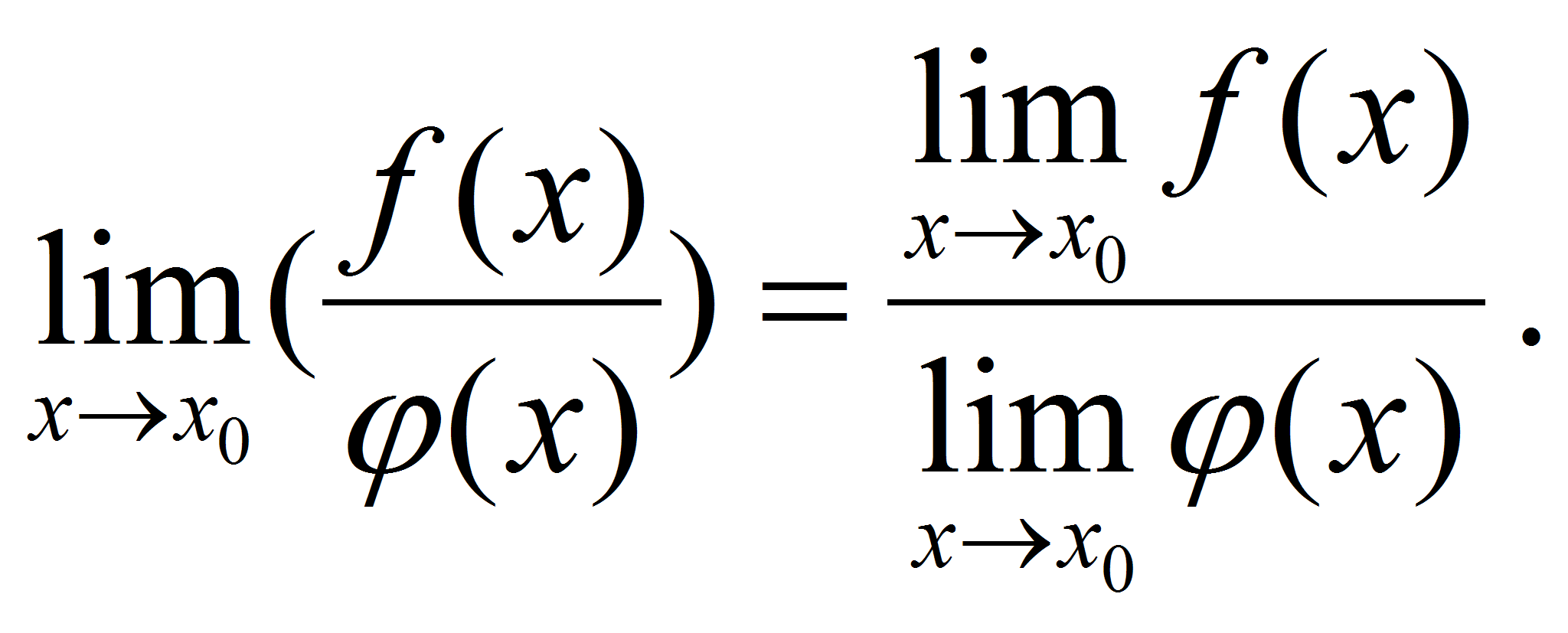
Теорема о пределе сложной функции (с доказательством).
-
Теорема о знакопостоянстве функции, имеющей ненулевой предел ( с доказательством).
Теорема:
Если
,
то существует окрестность точки а, в
которой
и знак
совпадает со знаком значения b.
Доказательство:
по
условию
,
т.е.
,
или
справедливы неравенства
.
Возьмём за
число
.
Тогда
,
,
являются числами одного знака.
Следовательно, в силу неравенства
,
и имеет знак числа b
в указанной
-окрестности
точки а.
-
Теорема о предельном переходе в неравенстве (доказательство для функции и последовательности).
-
Теорема о пределе промежуточной функции (доказательство для функции и последовательности).
Теорема
Пусть функции
и
имеет конечный предел А при
и пусть
тогда
Доказательство:
,
,
Рассмотрим
,
начиная с некоторого номера N
и
,
будут одинакого выполняться
.
Значит,
Предел промежуточной последовательности
-
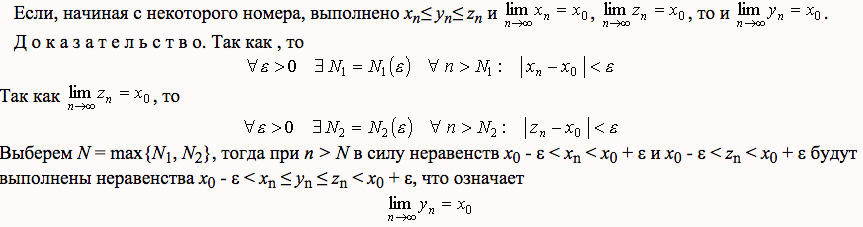
Первый замечательный предел (с выводом). Второй замечательный предел (вывод для функций с использованием теоремы Вейерштрасса для последовательностей).
Вывести 1 замечательный предел:
Пусть
,
.Проведем
геометрическое доказательство, основанное
на очевидном соотношении между тремя
площадями: Ясно, что
,
s2(сектор оab) но
,
т.е.
,
т.к.
.