
ИздательствоСанкт-Петербургский государственный лесотехнический университет имени С.М. КироваISBNГод2017Страниц18Уровень образованияМагистратура. Системный анализ
.pdf
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени С. М. Кирова»
Кафедра технологических процессов и машин лесного комплекса
СИСТЕМНЫЙ АНАЛИЗ
Методические указания и задания к курсовой работе магистров
по направлению подготовки 15.04.02 «Технологические машины и оборудование»
Санкт-Петербург
2017
1
Рассмотрены и рекомендованы к изданию Институтом технологических процессов и машин лесного комплекса
Санкт-Петербургского государственного лесотехнического университета 10 мая 2017 года
С о с т а в и т е л ь :
кандидат технических наук, доцент Е. Н. Власов
О т в . р е д а к т о р доктор технических наук, профессор В. А. Александров
Р е ц е н з е н т
кафедра технологических процессов и машин лесного комплекса СПбГЛТУ
Системный анализ: методические указания и задания к курсовой работе магистров по направлению подготовки 15.04.02 «Технологические машины и оборудование» / сост.: Е. Н. Власов. – СПб.: СПбГЛТУ, 2017. – 18 с.
Содержит методические указания и задание к курсовой работе «Анализ изменения скорости привода колонны лесного манипулятора в процессе торможения», которая является важным обобщающим этапом изучения курса «Системный анализ».
Предназначены для магистров по направлению подготовки 15.04.02 «Технологические машины и оборудование».
Темплан 2017 г. Изд. № 86.
2

ВВЕДЕНИЕ
Цель работы заключается в привитии студентам навыков математического моделирования и анализа на примере циклового гидропривода манипулятора лесопромышленного робота.
Курсовая работа выполняется в часы практических занятий, а также в часы самостоятельной работы. Под руководством преподавателя на практических занятиях разрабатывается линейная математическая модель циклового гидропривода лесопромышленного робота и проводится подготовка к моделированию на ЭВМ. Моделирование на ЭВМ динамики гидропривода выполняется студентами в часы самостоятельной подготовки.
После выполнения всех этапов отчет о проделанной работе студент защищает как курсовую работу.
I.ПОСТАНОВКА ЗАДАЧИ
Вкачестве объекта исследования выбран трехзвенный ангулярный манипулятор лесопромышленного робота с цикловой системой управления. Кинематическая схема манипулятора представлена на рис. 1.
Рис. 1. Кинематическая схема манипулятора
Задана типовая схема силовой части циклового гидропривода поворотной колонны (звена I) манипулятора (рис. 2). Поступательное движение штока гидроцилиндра преобразуется во вращательное движение колонны посредством зубчато-реечной передачи. Геометрические и инерционные параметры манипулятора, а также передаточное отношение зуб- чато-реечного механизма известны. Заданы конфигурации манипулятора. В качестве исследуемого режима работы гидропривода выбран наиболее ответственный режим - режим торможения, соответствующий останову поворотной колонны (звена I) манипулятора в заданной точке позиционирования.
3
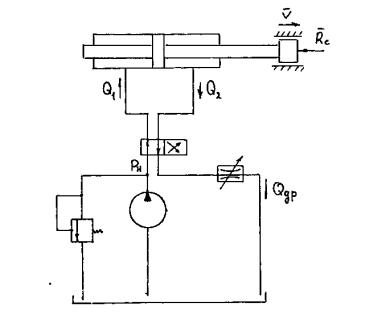
Рис. 2. Типовая схема силовой части циклового гидропривода поворотной колонны
Требуется разработать линейную математическую модель циклового гидропривода и методом моделирования на ЭВМ провести анализ работы привода при различных ускорениях торможения и различных конфигурациях манипулятора.
2. ИСХОДНЫЕ ДАННЫЕ
Геометрические и инерционные параметра манипулятора, а также значения обобщенной скорости колонны (звена I) при установившемся движении для каждого варианта задания представлены в таблице /I/.
Конфигурации манипулятора:
q2 |
0 const |
, |
q3 |
0, / 6, / 3, / 2 |
; |
|
||
|
|
|
|
|
|
|
||
q2 |
/ 6 const |
, |
q3 |
0, / 6, / 3, / 2 |
; |
|||
|
|
|
|
|
|
|
||
q2 |
/ 3 const |
, |
q3 |
0, / 6, / 3, / 2 |
. |
|||
|
|
|
|
|
|
|
||
Передаточное отношение зубчато-реечной передачи i=5, ход поршня
S=0,63 м, площадь поршня F 2 *10 2 м2 и давление питания Pн=10 МПа для всех вариантов одинаковы. Масса манипулятора 800 кг. Анализ работы
гидропривода проводится при двух значениях времени торможения |
tT |
|
(0,1 с.; 0,5 с.).
Исходные данные выбираются по первой букве фамилии студента из таблицы 1.
4

3. ЛИНЕЙНАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЦИКЛОВОГО ГИДРОПРИВОДА
При установившемся движении усилие на штоке гидроцилиндра равно усилию сопротивления Rc, включающему все силы, приложенные к штоку. При выдвижении штока выполняется равенство
Rg Fp1 Fp2 |
F ( p1 p2 ) Fpg , |
(1) |
где F – эффективная площадь поршня; р1, р2- давление в полостях гидроцилиндра, pg- расчетный перепада давления в гидроцилиндре.
Расходы в напорной Q1 и сливной Q2 полостях соответственно равны Q1 =vF, Q2 =vF , где v - скорость поршня гидроцилиндра.
При дроссельном регулировании скорости с дросселем на выходе скорость поршня v определяется расходом через дроссель Qgp. Здесь
Q f |
2 |
P Q Q |
|
|
|
2 |
|
||
qp |
|
qp 1 |
|
|
|
|
, |
(2) |
|
|
|
|
где μ - коэффициент расхода дросселирующего окна, μ= 0,71 при турбулентном течении рабочей жидкости; f - площадь проходного сечения рабочего окна; ρ - плотность рабочей жидкости, ρ =870 кг/м3, Pqp = p1 – p2 - перепад давления на дросселирующем окне; pсл - давление в сливной ма-
гистрали (рсл ≈ 0).
Пренебрегая объемными и гидравлическими потерями в магистралях и местных сопротивлениях, кроме потерь в дросселе, из уравнений (I) и (2) при р1 = рн получим
f |
|
2 |
|
( p p ) |
|
Q f |
|
2 |
( p p ) |
|
|
|
|
|
|
|
|
||||||
F |
|
|
н q |
|
qp |
|
н q |
|
|
||
|
|
или |
|
|
|
. |
(3) |
||||
|
|
|
|
|
|
|
|
|
|||
При неустановившемся движении уравнение движения поршнем гидроцилиндра согласно второму закону Ньютона, имеет вид
m |
|
|
dv |
F ( p |
p |
) R |
(4) |
п |
|
||||||
|
|
dt |
1 |
2 |
c |
|
|
|
|
|
|
|
|
|
где mn - приведенная к штоку масса подвижных частей манипулятора и предмета труда.
Найдем приведенную массу.
Кинетическая энергия манипулятора в общем случае складывается из кинетических энергий колонны, стрелы, рукояти и груза. Полагаем стрелу,
5

рукоять и колонну однородными стержнями, груз – точечной массой. Полагаем также, что ось вращения колонны совпадает с ее центром масс и можно пренебречь моментом инерции колонны относительно вертикальной оси. В результате кинетическая энергия колонны при ее вращении будет равна нулю.
Тогда, кинетическая энергия стрелы будет равна
|
Tct |
|
1 |
|
|
|
|
2 |
|
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
(J ct mct rct )q1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
J |
|
|
1 |
|
m l |
|
cos |
q , |
r |
lct |
cosq . |
||
|
|
|
|
|
2 |
2 |
|
|
|
|
||||
|
ct |
|
12 |
ct ct |
|
2 |
|
ct |
2 |
2 |
||||
|
|
|
|
|
|
|
|
|
|
|||||
В результате
Tct 12 q12 (13 mctlct2 cos2 q2 ) .
Кинетическая энергия рукояти будет равна
|
|
|
1 |
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Tp |
|
|
|
(J p mp rp |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
)q1 , |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
J p |
|
|
1 |
|
mp l p2 |
cos2 |
(q3 q2 ) , |
|
rp |
lct |
cosq2 |
|
1 |
l p cos(q3 q2 ) . |
|||||||
12 |
|
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
В результате |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
2 |
|
2 |
|
2 |
|
|
1 |
2 |
|
2 |
|
|
|
||||
|
Tp |
|
|
|
|
|
m p (lct |
cos |
|
q2 |
|
|
l p |
cos |
|
(q3 q2 )) . |
||||||
|
2 |
|
q1 |
|
3 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Кинетическая энергия груза будет равна
Tгр 12 q12 mгр (lct2 cos2 q2 l p2 cos2 (q3 q2 )) .
Суммируя полученные результаты, получаем выражение кинетической энергии манипулятора при его движении с помощью гидропривода колонны
T 12 q12 mпр ,
где mпр – приведенная к оси вращения колонны масса манипулятора с грузом.
6

|
|
1 |
2 |
2 |
|
|
|
2 |
|
2 |
|
|
1 |
2 |
|
2 |
|
|
|
mпр |
|
|
mctlct |
cos |
q2 |
m p |
(lct |
|
cos |
|
q2 |
|
|
l p |
cos |
|
(q3 |
q2 )) |
|
3 |
|
|
3 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mгр (lct2 cos2 q2 l p2 cos2 (q3 q2 ))
Приведем массу mпр к штоку гидроцилиндра привода колонны. Для этого перейдем от угловой скорости q1 вращения колонны к скорости v движения штока гидроцилиндра привода колонны
v qi1 .
Таким образом приведенная масса mп манипулятора к штоку гидроцилиндра привода колонны будет равна
mп i2 mпр .
Уравнение расходов в напорной магистрали с учетом сжимаемости жидкости
|
Q1 Qq Qсж , |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Qсж |
|
V 1 |
|
dp1 |
|
|
|
|
|
|
|
|
|
|
|
F |
dt - |
||||
где Qq = vF - расход, обусловленный перемещением поршня; |
|
||||||||||||||
расход на компенсацию сжимаемости рабочей жидкости; |
|
|
|
|
|
||||||||||
E 15 108 Па - модуль объемной упругости жидкости; V1 - объем жидко- |
|||||||||||||||
сти в левой полости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда получим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q F |
V1 |
|
|
dp1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
E |
|
dt . |
(5) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
Уравнение расходов в сливной магистрали по аналогии имеет вид |
|
|
|||||||||||||
Q F |
V2 |
|
|
dp2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
E |
|
dt , |
(6) |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
где V2 - объем жидкости в правой полости.
Приняв допущение V1 = V2 = V, сведем уравнения (5) и (6) к одному:
Qq F V0 dpq 2E dt ,
где V0 - половина всего объема гидроцилиндра.
Уравнение сохранения объемного расхода запишем в виде Qq = Qqp, где Qqp - расход рабочей жидкости через дроссель.
7

Предполагая, что подача и давление насосной установки постоянны (Qн = const, pн = const), а также, что усилие сопротивления мало (Rc ≈ 0), математическая модель привода сводится к системе из четырех уравнений:
|
mn |
d |
Fpq |
|
|||||||
|
|
|
|
|
|||||||
dt |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
V |
dpq |
|
||||
|
Q F |
|
|||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
q |
|
|
|
|
2E |
dt |
|
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|
||
Qqp f |
|
|
|
|
( pн |
pq ) |
|
||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
Qqp |
|
|
|
|
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
. |
(7) |
||
|
|
|
|
|
|
|
|
||||
Данная система уравнений, описывающая с учетом принятых допущений основные процессы в гидроприводе, нелинейная. Для получения линейной математической модели необходимо линеаризовать функцию (3), описывающую расходно-перепадную характеристику дросселя.
Линеаризация уравнений
Пусть некая система (подсистема), например, имеет входные величины х1, х2, выходную – х3 и внешнее воздействие f, а уравнение системы (подсистемы) имеет произвольный нелинейный вид
F(x , x |
2 |
, x |
2 |
, x , x |
, x |
, x ) ( f , f ) |
(8) |
|
1 |
|
3 |
3 |
3 |
3 |
|
||
(для примера взят определенный порядок входящих в уравнение производных x2, x3, f; вообще же здесь могут быть любые другие варианты).
Допустим, что установившийся процесс в системе имеет место при
некоторых |
постоянных значениях |
x |
x0 |
, |
x |
2 |
x 0 , |
x |
3 |
x 0 |
, |
f f 0 . |
Тогда |
|
|
|
|
1 |
1 |
|
|
2 |
|
3 |
|
|
|
||
уравнение установившегося состояния для данной системы будет |
|
|||||||||||||
F (x 0 |
, x 0 |
,0, x0 ,0,0,0) ( f 0 ,0) . |
|
|
|
|
|
(9) |
|
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
В основе линеаризации нелинейных уравнений, рассматриваемых здесь, лежит предположение о том, что в исследуемом динамическом процессе переменные (в данном случае х1, х2, х3) изменяются так, что их от-
клонения от установившихся значений |
(x0 |
, x0 , x0 ) остаются все время доста- |
||||||||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
точно малыми. |
|
|
|
|
|
|
|
|
|
|
||
Обозначим указанные отклонения через |
|
х1, х2, х3. Тогда в дина- |
||||||||||
мическом процессе |
|
|
|
|
|
|
|
|
|
|
||
x (t) x0 |
x (t), |
x |
2 |
(t) x0 x |
2 |
(t), |
x |
2 |
x |
2 |
, |
|
1 |
1 |
1 |
|
2 |
|
|
|
|
||||
8
x |
3 |
(t) x0 |
x |
3 |
(t), |
x |
3 |
x |
3 |
, |
x |
x |
, |
x |
x . |
|
3 |
|
|
|
|
|
3 |
3 |
|
3 |
3 |
Условие достаточной малости динамических отклонений переменных от некоторых установившихся значений для рассматриваемой в методических указаниях системы выполняются.
Внешнее воздействие f не зависит от работы системы, изменение его может быть произвольным, и поэтому правая часть нелинейного уравнения обычно линеаризации не подлежит.
Разложим функцию F, стоящую в левой части нелинейного уравнения, в ряд по степеням указанных выше малых отклонений, рассматривая все производные тоже как самостоятельные переменные. Тогда исходное нелинейное уравнение примет вид
|
|
|
|
|
|
F |
0 |
|
|
F |
0 |
|
|
|
|
F |
|
0 |
|
|
|
|||||||||
F (x0 , x0 ,0, x0 ,0,0,0) |
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|||||||||
|
|
|
|
|
|
|
x |
|
|
|
||||||||||||||||||||
1 |
2 |
3 |
|
|
|
x |
|
1 |
|
x |
|
|
2 |
|
|
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|||||||
|
|
F |
|
0 |
|
F |
0 |
|
|
F |
|
0 |
|
|
|
F |
|
0 |
|
|
||||||||||
|
|
|
|
|
x3 |
|
|
|
|
x |
3 |
|
|
|
|
|
x3 |
|
|
|
|
|
|
x3 |
|
|||||
|
x |
|
x |
|
x |
x |
||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||
(члены высшего порядка малости) = ( |
f , |
|
f ), |
|
(10) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
F |
0 |
|
|
где |
через |
|
|
|
|
|
для |
||||
|
x |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x x0 |
, |
x |
2 |
x |
0 , |
x |
2 |
0, |
|||
1 |
1 |
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
F |
|
|
|
краткости |
обозначена величина |
|
|
|
, взятая при |
||||
x |
|||||||||
|
|
||||||||
x3 |
x3 , |
…, |
x3 0 |
|
|
1 |
|
|
|
(т. е. сперва берется в общем виде |
|||||||||
|
0 |
|
|
|
|
|
|
|
|
частная производная от функции F по х1, после чего в нее вместо всех переменных подставляются их постоянные значения х10, х20, 0 , х30, …, 0).
Следовательно, все частные производные в полученном уравнении представляют собой некоторые постоянные коэффициенты. Они будут переменными во времени, если функция F содержит t в явном виде или если
установившийся процесс в системе определяется переменными значения-
ми х10 (t), x20 (t), x30 (t).
Члены высшего порядка малости, указанные в уравнении, состоят из произведений и степеней малых отклонений х1, х2, … с коэффициентами в виде смешанных частных производных и частных производных второго и высших порядков от функции F по всем переменным.
Вычтя из уравнения (10) почленно уравнение установившегося состояния (9) и отбросив члены высшего порядка малости, получим искомое линеаризованное уравнение динамики данной системы, взятой в качестве примера, в виде
|
F |
0 |
|
|
F |
0 |
|
|
F |
|
0 |
||
|
|
|
x1 |
|
|
|
|
x2 |
|
|
|
|
x2 |
x |
x |
|
x |
|
|||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
||
9

|
|
F |
0 |
|
|
|
F |
0 |
|
|
|
F |
0 |
|
|
|
F |
0 |
|
|
0 |
|
|
||
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,0). |
(11) |
||
|
|
|
|
|
|
|
|||||||||||||||||||
|
x |
|
|
|
x |
|
|
x3 |
|
x |
|
x3 |
|
x |
|
x3 |
= ( f , f ) ( f |
|
|||||||
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
||
Это дифференциальное уравнение, так же как и (8), описывает тот же динамический процесс в той же системе. Отличие этого уравнения от прежнего состоит в следующем:
1) это уравнение является более приближенным, ибо в процессе его вывода были отброшены малые слагаемые высшего порядка;
2) неизвестными функциями времени в этом уравнении являются не прежние полные величины х1, х2, х3, а их отклонения х1, х2, х3 от некоторых установившихся значений х10, х20, х30;
3) полученное уравнение является линейным относительно откло-
|
x1 , |
|
|
|
x |
, |
|
x |
|
F |
0 |
|
нений |
x2 , |
x2 |
, |
3 |
|
…, |
3 |
|
|
|
, |
|
|
|
|
|
|
|
|
с постоянными коэффициентами |
x |
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
F 0
, … (или с переменными коэффициентами, если F содержит t в яв-
x2
ном виде, а также когда установившийся процесс определяется перемен-
ными величинами х10 (t), x20 (t), x30 (t).
Таким образом, цель получения линейного дифференциального уравнения взамен прежнего нелинейного достигнута.
В дальнейшем можно проводить линеаризацию нелинейных уравнений непосредственно по аналогии с формулой (11), не производя предварительных выкладок.
Принято записывать дифференциальные уравнения так, чтобы выходная величина и ее производные находились в левой части уравнения, а входная величина и все остальные члены – в правой части. Кроме того, принято, чтобы сама выходная величина входила в уравнение с коэффициентом единица. Чтобы привести линеаризованное уравнение (11) к такому виду, введем обозначения:
|
|
|
F |
|
0 |
|
F |
|
0 |
|
|
|
|
F |
|
0 |
|
|
|
|
F |
|
0 |
|||||||||||||||||||
k1 |
|
|
|
|
|
|
: |
|
|
|
|
|
|
, |
k2 |
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
, |
||||||||||
x |
|
x |
|
|
|
|
x |
|
|
|
x |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
F |
0 |
|
|
|
F |
0 |
|
|
|
|
|
|
F |
0 |
|
|
|
|
|
|
|||||||||||||||||||
k |
3 |
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
, |
k |
4 |
1 |
: |
|
|
|
|
|
|
|
, |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x2 |
|
|
|
x3 |
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(12) |
|
|
F |
|
0 |
|
|
F |
|
|
0 |
|
|
|
|
F |
|
|
0 |
|
|
F 0 |
|
|
|||||||||||||||||||
T |
|
|
|
|
|
: |
|
|
|
|
|
|
|
, |
T 2 |
|
|
|
|
: |
|
|
|
|
|
, |
|
|||||||||||||||
|
1 |
x |
|
|
|
|
x |
|
2 |
|
x |
|
|
|
|
x |
|
|
||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
||||||||||||||||||
10
