3. Основные законы распределения

• Распределение Гаусса (нормальное распределение).

• Распределение Пирсона.

• Распределение Стьюдента.

• Распределение Фишера.

• Экспоненциальное и логнормальное распределения.

• Равномерное и треугольное распределения.

3.1. Распределение Гаусса (нормальное распределение)

Наиболее широко применяемое распределение. Нормальное распределение является краеугольным камнем математической статистики в силу ряда причин:

– схема его возникновения соответствует многим реальным физическим процессам, порождающим результаты обрабатываемых наблюдений;

– при возрастании объема выборки предельное распределение для большинства распределений является нормальным и с успехом может использоваться для аппроксимации последних;

– нормальное распределение обладает рядом благоприятных математико-статистических свойств (легко нормируется и аппроксимируется, обладает свойством аддитивности).

Обозначение
Параметры
Плотность вероятности
Функция распределения
Среднее
Дисперсия
Стандартное отклонение
Коэффициент вариации
Коэффициент асимметрии	0
Коэффициент эксцесса	0
Медиана

Для удобства в практических задачах используется нормированная случайная величина , распределение которой называется нормированным нормальным распределением (или стандартным нормальным распределением) .

Значение дифференциальной функции стандартного нормального распределения по заданному вычисляется непосредственно по формуле

.

Для интегральной же функции нормированного нормального распределения в справочниках приводятся таблицы значений функции

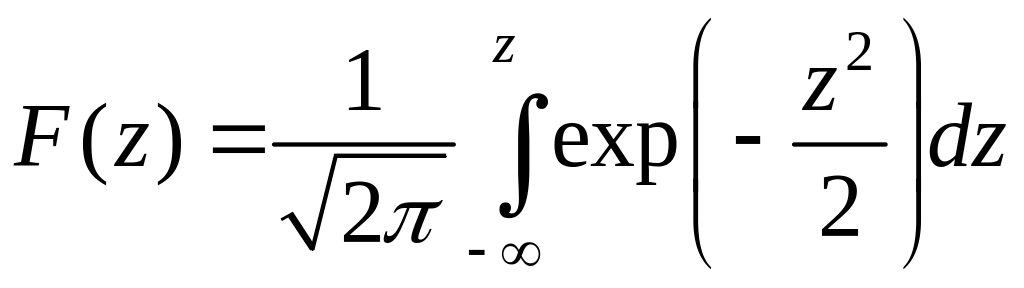
или связанной с ней функции Лапласа

.

Аналитическое выражение для функции Лапласа имеет вид

.

Функцию Лапласа также используют в виде

.

Поскольку таблицы всегда ограничены и их сложно применять при автоматизации статистической обработки экспериментальных данных, то применяется аппроксимация для функции

Вычислив значение интегральной функции стандартного нормального распределения, можно получить значение функции Лапласа, воспользовавшись соотношением .

Пример Вычислить значения интегральной функции нормированного нормального распределения и функций Лапласа в точке . Решение: По формуле вычисляем значение . По формуле определяем , тогда .

В практических задачах возникает необходимость вычисления p-квантили нормального распределения (то есть такого значения нормально распределенной случайной величины, которое с вероятностью p не превзойдут другие значения этой случайной величины). Квантиль можно вычислить с помощью p-квантили стандартного нормального распределения по формуле

.

Квантиль можно вычислить с помощью аппроксимации

.

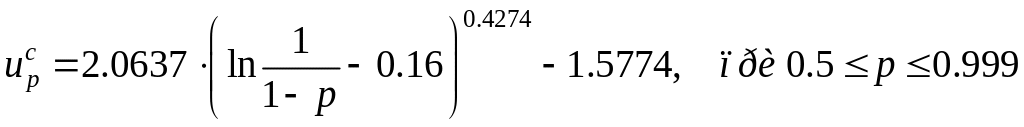Для вычисления квантили при нужно учитывать свойство симметричности стандартного нормального распределения

.

Некоторые методы статистики используют понятие верхнего квантиля функции Лапласа (обозначается ). Его значение можно вычислить по формуле

Пример Вычислить значение случайной величины, распределенной по стандартному нормальному закону, вероятность превышения которого равна 0.05. Вычислить значение верхнего квантиля функции Лапласа при p=0.9. Решение: Если перефразировать условие задачи, то нужно вычислить такое значение случайной величины, чтобы остальные значения случайной величины были меньше с вероятностью , то есть требуется вычислить квантиль . По формуле . Верхний квантиль функции Лапласа определяется по формулам и .