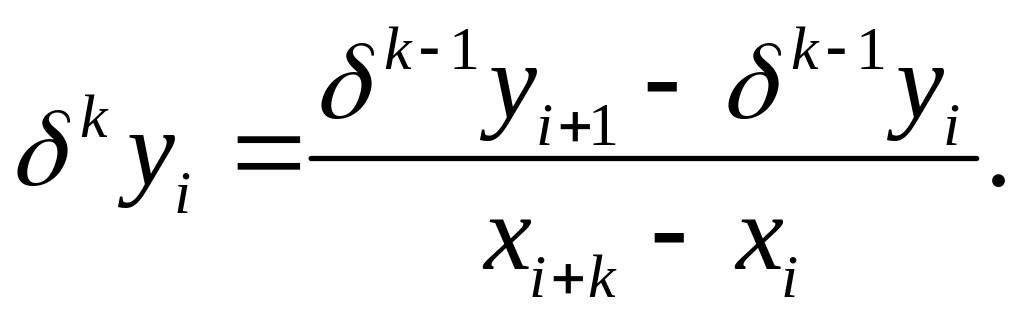- •Аннотация
- •1. Основы теории измерений
- •1.1. Понятия “эксперимент” и “экспериментальные данные”. Источники и пути повышения точности экспериментальных данных
- •1.2. Основные понятия и определения теории измерений
- •1.3. Классификация погрешностей результатов измерений
- •2. Основы теории вероятностей и математической статистики
- •2.1. Случайная величина. Интегральная и дифференциальная функции распределения случайной величины и их свойства.
- •2.2. Генеральная и статистическая (выборочная) совокупности. Статистический ряд и способы его представления
- •2.3. Статистические (эмпирические) функции распределения
- •2.4. Статистические оценки параметров распределения случайной величины и их свойства
- •2.5. Статистические гипотезы
- •3. Основные законы распределения
- •3.1. Распределение Гаусса (нормальное распределение)
- •3.2. Распределение Пирсона
- •3.3. Распределение Стьюдента
- •3.4. Распределение Фишера
- •3.5. Экспоненциальное и логнормальное распределения
- •3.6. Равномерное и треугольное распределения
- •4. Обработка результатов прямых многократных измерений
- •4.1. Понятие о прямых многократных измерениях. Общий алгоритм обработки результатов наблюдений
- •4.2. Оценки центра распределения результатов наблюдений, оценка результата измерения
- •4.3. Моменты случайной величины и их оценки, оценки стандартных отклонений результатов наблюдений и результата измерения
- •4.4. Коэффициенты формы закона распределения случайной величины и их оценки
- •4.5. Устранение грубых ошибок прямых многократных измерений
- •4.5.1. Исключение промахов проверкой статистических гипотез
- •4.5.2. Исключение промахов универсальным методом
- •4.6. Исключение переменной составляющей систематической погрешности
- •4.7. Определение вида закона распределения результатов наблюдений
- •4.7.1. Определение вида закона распределения методом моментов
- •4.7.2. Критерии принадлежности результатов наблюдений к нормальному закону распределения
- •4.8. Интервальная оценка результата измерения
- •4.8.1. Определение доверительного интервала результата измерения
- •4.8.2. Определение границ случайной погрешности
- •4.8.3. Определение границ неисключенной систематической погрешности
- •5. Правила округления результатов измерений
- •6. Обработка результатов прямых однократных измерений
- •7. Обработка результатов неравноточных измерений
- •7.1. Понятие о неравноточных измерениях. Общий алгоритм обработки результатов неравноточных измерений
- •7.2. Проверка гипотезы о равенстве дисперсий
- •7.3. Проверка гипотезы о равенстве центров распределений
- •7.4. Определение точечной и интервальной оценок результата измерений
- •8. Обработка результатов косвенных измерений
- •8.1. Косвенные измерения. Коэффициент корреляции
- •8.2. Критерии значимости корреляционной связи
- •8.3. Определение стандартного отклонения результата измерения
- •8.4. Определение доверительного интервала результата измерения
- •9. Основы теории интерполяции
- •9.1. Основные понятия и определения теории интерполяции
- •9.2. Интерполяция точная в узлах
- •9.2.1. Конечные и разделенные разности
- •9.2.2. Интерполяция кусочно-линейными функциями
- •9.2.3. Интерполяция полиномами
- •9.3. Аппроксимация
- •9.3.1. Наиболее часто используемые функции
- •9.3.2. Методы выбора аппроксимирующей функции
- •9.3.3. Методы аппроксимации
- •10. Обработка результатов совместных измерений
- •10.1. Понятие о совместных измерениях и регрессии. Задачи статистического исследования регрессии
- •Статистический анализ коэффициентов регрессии.
- •10.2. Регрессия элементарными функциями
- •10.3. Регрессия полиномами
- •10.4. Статистический анализ коэффициентов регрессии
- •10.5. Устранение грубых ошибок измерения
- •10.6. Построение доверительной области регрессии.
- •10.7. Проверка соответствия уравнения регрессии экспериментальным данным
- •Вопросы к экзамену
- •Правила округления результатов измерений.
- •Понятие о неравноточных измерениях. Общий алгоритм обработки результатов неравноточных измерений.
- •Критерии значимости корреляционной связи.
- •Понятие о совместных измерениях и регрессии. Задачи статистического исследования регрессии.
- •Регрессия элементарными функциями.
- •Основные понятия и определения теории интерполяции.
- •Конечные и разделенные разности.
- •Интерполяция кусочно-линейными функциями.
- •Список рекомендуемой литературы
9. Основы теории интерполяции
Основные понятия и определения теории интерполяции.
Интерполяция точная в узлах.
Аппроксимация.
9.1. Основные понятия и определения теории интерполяции
Задача интерполяции
состоит в следующем. На некотором отрезке
заданы n
точек
![]() и значения некоторой функции
и значения некоторой функции
![]() в этих точках
в этих точках
![]() .
Требуется найти аналитический вид
функции
.
Требуется найти аналитический вид
функции
![]() ,
проходящей через эти точки.
,
проходящей через эти точки.
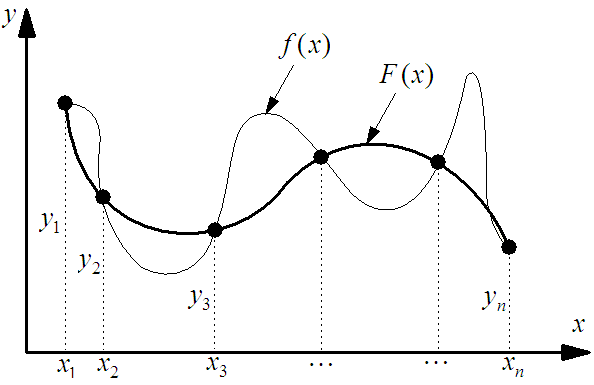
Точки
называются узлами
интерполяции,
функция
называется идеальной
функцией, а
функция
– интерполирующей
функцией. В
математической статистике
![]() называется уравнением
регрессии.
называется уравнением
регрессии.
Расстояние между узлами интерполяции называется шагом .
Если интерполирующая функция проходит через все заданные точки, то такая интерполяция называется точной в узлах. На практике же провести эксперимент без погрешностей невозможно, поэтому проводить интерполяцию точную в узлах часто бывает нецелесообразно. Тогда используется интерполяция, приближенная в узлах (аппроксимация).
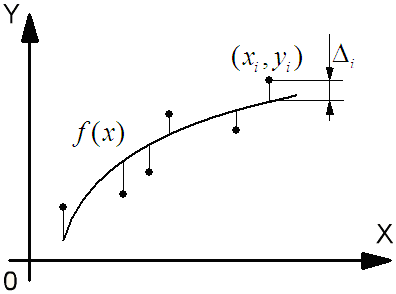
![]() – уклонение
(разность в i-ой
точке между значением аппроксимирующей
функции и экспериментальным значением,
т.е.
– уклонение
(разность в i-ой
точке между значением аппроксимирующей
функции и экспериментальным значением,
т.е.
![]() ).
В математической статистике уклонение
называется регрессионным
остатком.
).
В математической статистике уклонение
называется регрессионным
остатком.
Задача аппроксимации – поиск такой функции , которая в узлах мало бы отличалась от экспериментальных значений. Критериями близости могут быть:
1. Равенство нулю алгебраической суммы всех уклонений, т.е.

2. Сумма квадратов уклонений минимальна, т.е.
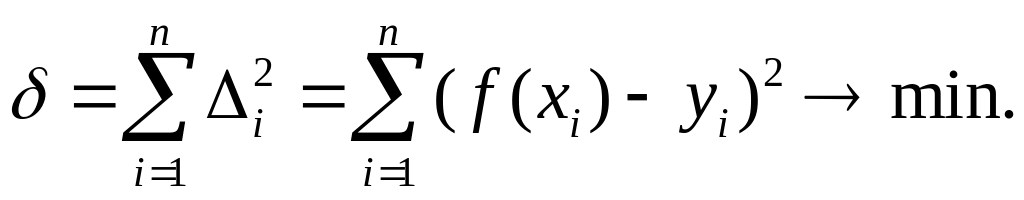
3. Среднее значение всех уклонений минимально, т.е.
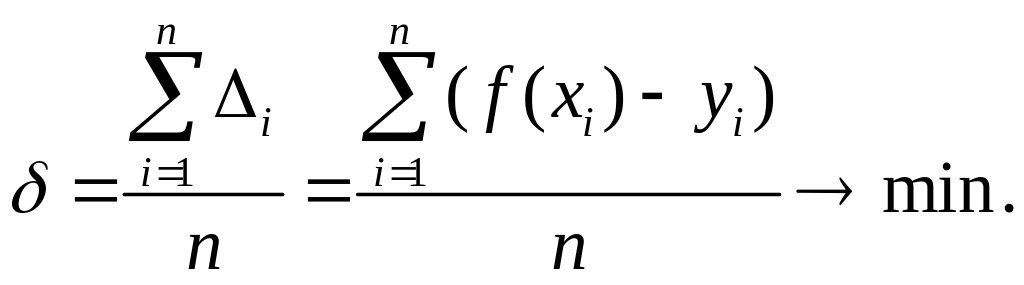
Если найдена
функция
,
то по ней можно приближенно вычислить
значение идеальной функции
в точках х,
отличных от узлов. При этом различают
интерполирование
в узком смысле, когда
![]() ,
и экстраполяцию,
когда
,
и экстраполяцию,
когда
![]() .
В статистике экстраполяция называется
также прогнозом.
.
В статистике экстраполяция называется
также прогнозом.
9.2. Интерполяция точная в узлах
9.2.1. Конечные и разделенные разности
Если значения
идеальной функции в узлах интерполяции
![]() ,
то конечные
разности первого порядка
определяются по формулам
,
то конечные
разности первого порядка
определяются по формулам
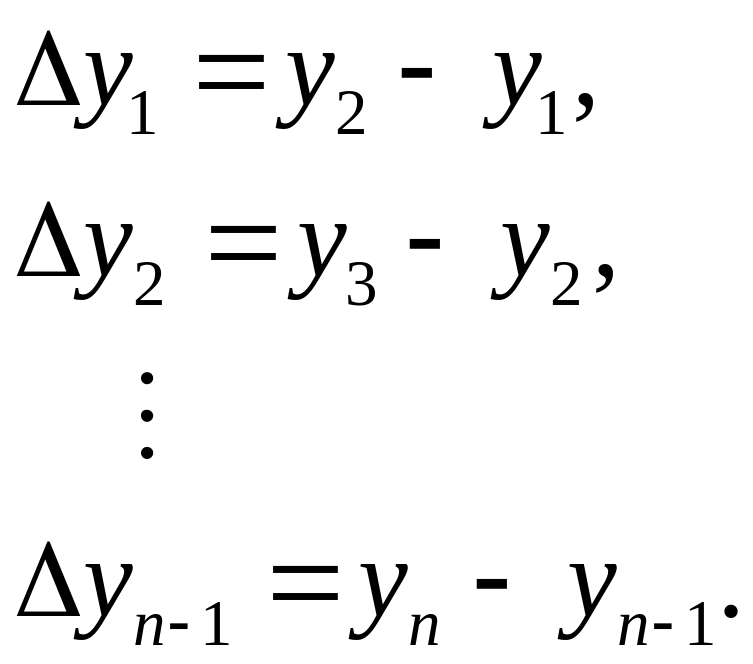
Конечные разности второго порядка
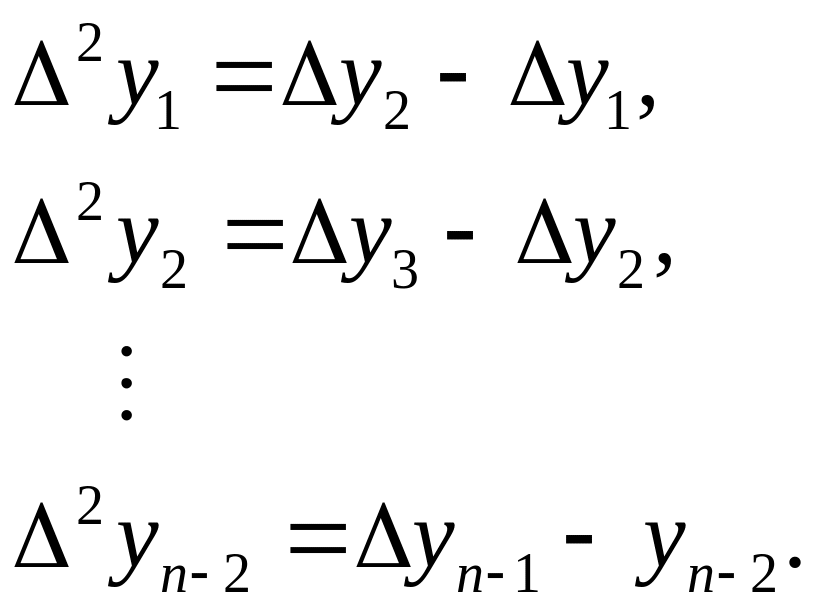
Аналогично
определяются конечные разности следующих
порядков. Общее количество конечных
разностей i-ого
порядка равно
![]() .
.
Если за начальную точку взять значение идеальной функции в середине таблицы экспериментальных данных, то конечные разности будут называться центральными разностями.
Пример Конечные разности:
Центральные разности:
|
В общем случае конечные и центральные разности определяются по формуле
![]()
Разделенные разности первого порядка определяются по формулам
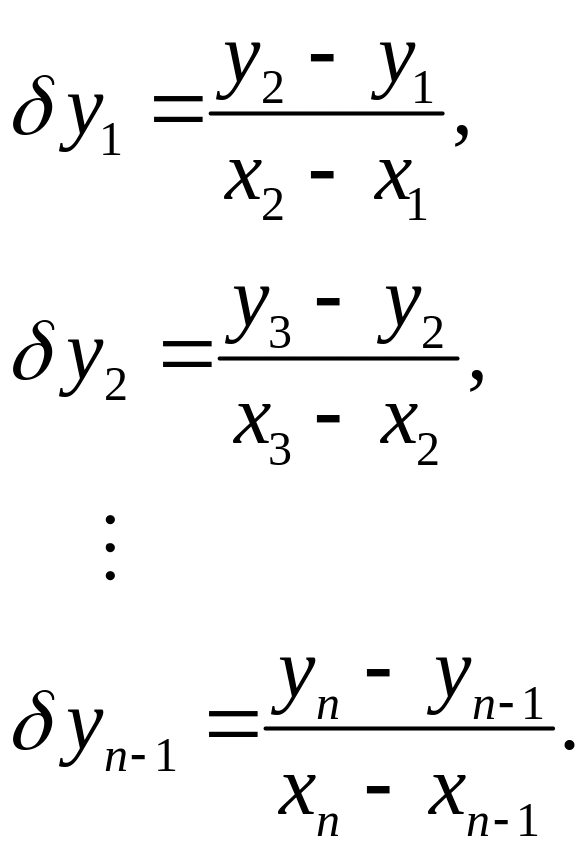
Разделенные разности второго порядка
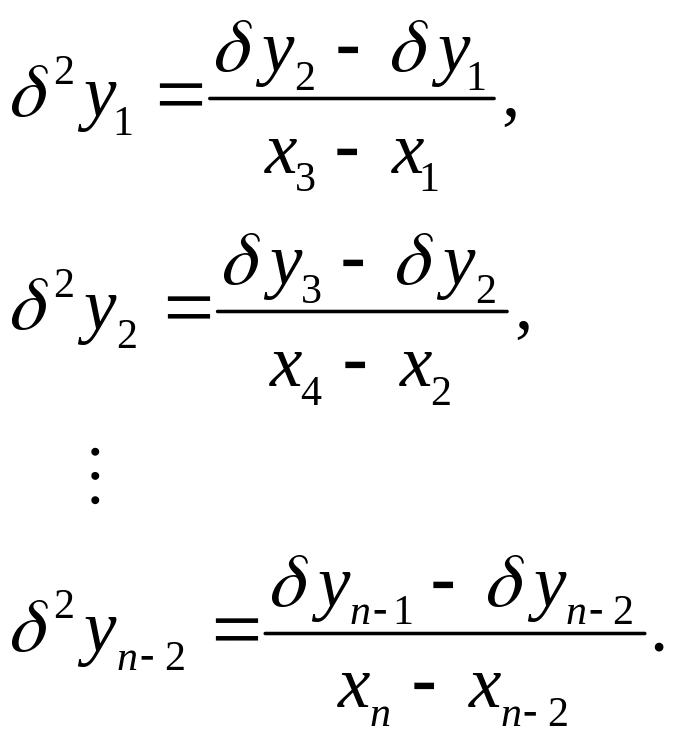
В общем случае разделенные разности определяются по формуле